4.9: Protein Stability - Thermodynamics
- Page ID
- 47177
Introduction to Protein Stability
This material is not easy, and is perhaps the most intellectually challenging of the entire book. Much of the organizational framework for this section comes from an article by Ken Dill, Biochemistry, 29, 7133-7155 (1990) as that article so clearly defined the factors that contribute to protein stability.
Extrapolating from the results of studies of the transfer of small molecule H bond donors/acceptors and hydrophobic molecules from water to nonpolar solvents, it would appear that H bond interactions (as well as ion ..ion interactions) do not drive protein folding per se. Rather, the biggest contributors to the stabilization of the native state are the hydrophobic effect and the van der Waals interactions among the tightly packed buried atoms of the protein. However, using actual data from wild-type and mutant proteins of known structure, it appears that H bonds contribute significantly to protein folding and stability, and may make a greater contribution to the stability of the native state than the hydrophobic effect. The main factor which opposes folding is chain conformational entropy as folding proceeds from very populated denatured states to a "single" folded state. These positive and negative factors sum up to a small negative ΔG favoring protein folding, implying marginal stability of the native protein at normal temperatures.
What types of noncovalent forces might act within a protein and between proteins and solvent molecules that would cause a protein to fold spontaneously to a unique 3D structure? These forces can be long range (ion-ion, ion-dipole, or dipole-dipole) or short range (van der Waals repulsive and attractive forces). The interactions can be local (between adjacent amino acids in the linear sequence) or nonlocal (between sequences separated in the linear sequence but brought close together in 3D space). Clues as to what stabilizes the tertiary structure of a native protein can be gained by subjecting proteins to agents that unfold or denature proteins. Such agents include extremes of pH, high concentrations of some salt solutions or organic solvents, and temperature extremes. Such experiments show that native proteins are only marginally stable (about 0.4 kJ/mol amino acid - or around - 10 kcal/mol (-42 kJ/mol) for a protein of molecular weight of 10,000 - about 100 amino acids). This is equivalent to the stability provided by 2 H bonds. We will consider the different types of noncovalent attractions (ion-ion, H bonds, van der Waals), and stabilizing influences arising from the hydrophobic effect. and ask if each is a significant driving force for protein folding. Figure \(\PageIndex{1}\) shows the relative contributions to the ΔG for protein folding.
Most of this chapter will deal with H bonding and the hydrophobic effect. A theme of any biochemistry course is that if you can understand the interactions among small molecules, you can apply that knowledge to the understanding of larger molecules like proteins. To understand if H bonds within proteins, often buried in the more hydrophobic interior of the protein, drive protein folding, we will first examine the thermodynamics of H bond formation of a small molecule, N-methylacetamide, in water and in a nonpolar solvent. To understand if the hydrophobic effect, mediated by the burying of nonpolar side chains within the more nonpolar center of the protein, drives protein folding, we will examine the thermodynamics of benzene solubility in water. Most recent studies involve the creation of specific mutants at amino acid positions that might reveal the contributions of H bonding and the hydrophobic effect to folding and protein stability.
Ion - Ion Interactions
These could be investigated by altering pH or ionic strength. Why is that?
a. General Charge Interactions - Proteins denature at either low or high pHs where they have a maximal positive charge or negative charge, respectively. Small proteins that seem to fit a simple two-state folding model (F ↔ U) have a characteristic melting temperature (TM) at which the 50% of the proteins in the population are unfolded. The higher the TM, the more stable the protein. The graphs of the TM for different proteins at different pH values are shown in Figure \(\PageIndex{2}\).
Under extremes of pH (but not so great as to catalyze peptide bond cleavage, electrostatic repulsions would cause the protein to denature. The folded, compact state has an increasing charge density (q/Vol) at pH extremes, which could be alleviated by unfolding to a less dense state. But what about specific charge pair interactions? In contrast to the general charge interactions, these might actually stabilize a protein. Are they the predominant factor that determines stability?
b. Specific Charge Interactions (charge pairs) - If ion pairs are the source of protein stability, you would expect that high salt could disrupt them, and lead to denaturation. Although some salts do denature proteins, others stabilize them. Other evidence argues against this idea. Ion pairs are not conserved in evolution. In addition, the number of ion pairs in proteins is small (approx. 5/150 residues, with one of those on average buried). Also, the stability of a protein shows little dependence on pH or salt concentration (at low concentrations) near the isoelectric point, the pH at which proteins have a net zero charge.
The overall charge state affects not only the stability of a protein but also its solubility. Proteins are most insoluble at their isoelectric point pI since at that pH value (where they have a net 0 charge) the proteins experience the least electrostatic repulsion and are most likely to aggregate and precipitate. Low salt concentration also promotes insolubility. Mutagenesis studies show that solubility can be increased by replacing nonpolar groups on the surface with polar ones. Pace (2009) cites studies on RNase Sa which has a maximally exposed Thr 76. If it is replaced with aspartic acid, the solubility increased to 43 mg/ml but if it is replaced with tryptophan, it decreased to 3.6 mg/ml. His, Asn, Thr and Gln have a negative effect on solubility near the pI compared to Ala, a surprising result. Similar results were obtained compared to Ala when Arg and Lys were used. Smaller side chains, Asp and Ser, at position 76 increased the solubility over Ala.
Hydrogen Bonding
Linus Pauling first suggested that H bonds (between water and the protein and within the protein itself) would play a dominant role in protein folding and stability. It would seem to make sense since amino acids are dipolar and secondary structure is common. Remember, however, the H bonds would be found not only in the native state but also in the denatured state. Likewise, there are H bonds between water and proteins in both the native and denatured states. Do H bonds in proteins contribute differently to the stability of the D vs N states? Many experimental and theoretical studies have been performed investigating helix ↔ (random) coil transitions in small peptides. Remember all the intrachain H bonds in the helix? Are they collectively more stable than H bonds between water and the peptide in a (random) coil?
In this section, we will explore the effects of H bonds on small molecules and infer from them the likely contributions of H bonds to protein stability. After all, if we can't understand small molecules and their interaction, how can we understand the same interactions in big ones like proteins? We will see however that when we use modern tools of site-directed mutagenesis to explore H bonds in proteins, we come to different conclusions as to their relative roles. So consider this immediate section an exercise in model building and critical thinking.
In thinking about conformational studies involving small peptides, it is useful to apply Le Chatelier's Principle to the equilibrium below:
random coil ↔ helix
Anything perturbant (small molecules, solvent, etc) that would preferentially interact with the helical form would push the equilibrium to the helical form.
Early models assumed that intrachain H bonds were energetically (enthalpically) more favorable than H bonds between peptide and water. But to form a hydrogen bond requires an entropy payback since a helix is much more ordered (lower entropy) than a random coil (higher entropy). At low temperatures, enthalpy predominates and helix formation in solution is favored. At high temperatures, the helix is disfavored entropically. Imagine the increased vibrational and rotational states permitted to the atoms at higher temperatures. Theoretical studies on helix-coil transitions predicted the following:
- as the chain length increases, the helix gets more stable;
- increasing the charge on the molecule destabilizes the helix, since the coil, compared to the more compact helix, has a lower charge density;
- solvents that protonate the carbonyl oxygen (like formic acid) destabilize the helix; and
- solvents that form strong H bonds compete with the peptide and destabilize the helix. In contrast, solvents such as CHCl3 and dimethylformamide (a nonprotic solvent), stabilize the helix. Likewise, 2-chloroethanol and trifluoroethanol, which form none or weaker H bonds to the peptide than water, stabilize the helix. (In the case of trifluoroethanol, molecular dynamics simulations have shown that TFE preferentially interacts with (solvates) the peptide, which inhibits H bonds from the peptide backbone to water, stabilizing the intrahelical H bonds.
These helix-coil studies suggest that H bonds are important in stabilizing a protein.
But do they really? Why should these H bonds differ from those in water? It's difficult to figure out whether they are since there are so many possible H bonds (between protein and water, water and water, and protein and protein), and their strength depends on their orientation and the dielectric constant of the medium in which they are located.
If intrachain H bonds in a protein are not that much different in energy than intermolecular H bonds between the protein and water, and given that proteins are marginally stable at physiological temperatures, then it follows that the folded state must contain about as many intramolecular hydrogen bonds within the protein as possible intermolecular H bonds between the protein and water, otherwise the protein would unfold.
To resolve this issue, and determine the relative strength of H bonds between the varying possible donors and acceptors, many studies have been conducted to compare the energy of H bonds between small molecules in water with the energy of H bonds between the same small molecules but in a nonpolar solvent. The rationale goes like this. If the interior of a protein is more nonpolar than water (lower dielectric constant than water), then intrastrand H bonds in a protein might be modeled by looking at the H bonds between small molecules in nonpolar solvents and asking the question, is the free energy change for the following process less than zero:
Dw + Aw ↔ (DA)n, ΔGo, K
where D is a hydrogen bond donor (like the H in N-H) and A is a hydrogen bond acceptor, (like the O in C=O), w is water (i.e. donor and acceptor are in water), and n is a nonpolar solvent, and ΔGo and K are the standard free energy change and the equilibrium constant, respectively, for the formation of a H-bond in a nonpolar solvent from a donor and acceptor in water. This reaction simulates H-bond contributions to protein folding, where a buried H-bond is mimicked by a H-bond in a nonpolar solvent. The reaction written above is really based on a thought experiment since it would be hard to set up the necessary conditions to make the measurement. However, we can calculate the ΔGo for this reaction since it is a state function and it really doesn't matter how one accomplishes this process.
You learned about state functions in introductory chemistry courses so this should not be a new concept. Remember a state function is one in which the variable describing two connected states does not depend on the path between the states. A simple example involves potential energy and height. Imagine you climb a mountain to the peak. It doesn't matter which path you take up the mountain, since the difference in height (Δ height) is the same if you start at the same point and end up at the peak. Your change in potential energy is also the same. ΔGo for protein folding is also a state function for a given set of conditions (temperature, pressure, solvent)
Let's consider a specific example, the formation of H bonds between two molecules of N-methylacetamide (NMA) in water and in a nonpolar solvent. N-methylacetamide is a good mimic for the H bond donors and acceptors of the peptide bond of a polypeptide chain as shown in Figure \(\PageIndex{3}\) below.
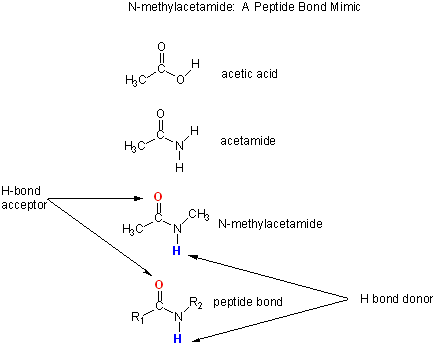
(\PageIndex{3}\): N-methylacetamide as a mimic for the peptide backbone
The reaction scheme shown in Figure \(\PageIndex{4}\) describes a set of reactions (a thermodynamic cycle) involving the formation of H-bonded dimers of NMA . A and B are both molecules of NMA, in either water (w) or a nonpolar solvent (n). N-methylacetamide is a good mimic for the H bond donors and acceptors of the peptide bond of a polypeptide chain as .
K1 is the equilibrium constant for the dimerization of NMA in a nonpolar medium. This can be readily determined, and is >1, implying that ΔGo < 0. (Remember, ΔGo = -RTlnKeq) For the dimerization of NMA in CCl4, ΔGo1 = -2.4 kcal/mol (-10 kJ/mol).
K2 is the equilibrium constant (think of it as a partition coefficient) for the transfer of two NMA molecules from water to a nonpolar solvent (again easily measurable). For NMA transferring from water to CCl4, ΔGo2 = + 6.12 kcal/mol (+25.6 kJ/mol).
K3 is the equilibrium constant for the dimerization of NMA in water. This can be readily be determined and is <1, implying that ΔGo > 0. For the dimerization of NMA in water, ΔGo3 = +3.1 kcal/mol (+13 kJ/mol).
K4 is the equilibrium constant (think of it as a partition coefficient) for the transfer of a hydrogen-bonded dimer of NMA from water to a nonpolar solvent. You try to think of a way to measure that! I can't. This is where thermodynamic cycles come in so nicely. You don't have to measure it. You can calculate it from K1-3 since ΔGo is a state function!
\begin{equation}
\begin{aligned}
&\Delta \mathrm{G}_{2}^{0}+\Delta \mathrm{G}^{0}{ }_{1}=\Delta \mathrm{G}_{3}^{0}+\Delta \mathrm{G}_{4}^{0} \text { or } \\
&-\mathrm{RTInK}_{2}+-\mathrm{RT} \ln \mathrm{K}_{1}=-\mathrm{RT} \ln \mathrm{K}_{3}+-\mathrm{RT} \ln \mathrm{K}_{4} \\
&\mathrm{InK}_{2}+\ln \mathrm{K}_{1}=\ln \mathrm{K}_{3}+\ln \mathrm{K}_{4}=\ln \left(\mathrm{K}_{2} \mathrm{~K}_{1}\right)=\ln \left(\mathrm{K}_{3} \mathrm{~K}_{4}\right) \text { or } \\
&\mathrm{K}_{2} \mathrm{~K}_{1}=\mathrm{K}_{3} \mathrm{~K}_{4}
\end{aligned}
\end{equation}
For NMA transferring from water to CCl4, ΔGo4 = + 0.62 kcal/mol (+2.6 kJ/mol).
(Note: Biochemists like to talk about thermodynamic cycles which may seem new to you. However, believe it or not, you have seen them before in introductory chemistry in the form of Hess's Law!)
From K1-4 and the corresponding ΔGo values, we can now calculate ΔGo5 for the formation of H-bonded NMA dimers in a nonpolar solvent from two molecules of NMA(aq). This reaction, which we hope simulates the formation of buried intrachain H bonds in proteins on protein folding, is:
Dw + Aw ↔ (DA)n, for which ΔGo5= +3.72 (i.e. disfavored).
If this model is a good mimic for studying H bond formation on protein folding, it suggests that the formation of buried H bonds during protein folding does not drive protein folding.
However, if the transfer of D and A (from a large protein) from water to the nonpolar medium (modeled by K2) is driven by other effects (such as the hydrophobic effect), the negative value for ΔGo1 will significantly favor buried H bond formation. So, if this happens in proteins, it is clear why so many intrachain H bonds form, since K1 is favored. H bonds may not assist the collapse of a protein, but would favor internal organization within a compact protein. That is, H bonds don't drive protein folding per se, but form so that the folded protein would not be destabilized by too many unsatisfied H bonds.
There are potential problems with this simple model. The interior of a protein is not homogeneous (i.e. the effective dielectric within the protein will vary). H bond strength is also very sensitive to geometry. Also, there are many H bonds within a protein, so slight errors in the estimation of H bond strength would lead to large errors in the determination of protein stability.
Another argument against H bonds being the determining factor in protein folding and stability comes from solvent denaturation studies. If intrachain H bonds are so important, then should not solvents that can H bond to the backbone denature the protein? Shouldn't water (55 M) act as a denaturant? It doesn't, however. Dioxane (5 membered heterocyclic ring with O) which has only a H bond acceptor wouldn't be expected to denature proteins, but it does. H bonds also increase in nonpolar solvents. Peptides, which have random structures in water, can be induced to form helices when placed in alcohol solutions (trifluorethanol, for example), which are more nonpolar than water, as explained above in the helix-coil studies. If H bonds are the dominant factor in protein stability, the alcohols would stabilize proteins. At low concentrations of alcohol, proteins are destabilized.
Hydrophobic Interactions: Introduction
We have studied the role of the hydrophobic effect (involving the favorable entropic release of caged water molecules about solvent-exposed hydrophobic groups) in driving nonpolar molecule solubility in Chapter 2.5. Does this also drive protein folding? To explore this question, we will study the thermodynamics of small nonpolar molecules, especially benzene, with water and ask whether the thermodynamic parameter associated with benzene solubility are similar to those associated with protein stability. If this analogy holds, anything that will promote benzene solubility will lead to increased hydrophobic amino acid side chain exposure to water and hence protein denaturation. What is the evidence to support this?
a. Crystal structures: PDB crystal structures show that most nonpolar side chains are buried inside a protein, which is tightly packed and which excludes water. Studies show that as the surface area of amino acid side chains increases, the free energy of transfer of amino acids from water to ethanol becomes more negative as shown in Figure \(\PageIndex{5}\).
b. Low-temperature denaturation of proteins - It has been observed that proteins can denature at low temperatures (less than 0o C), suggesting that nonpolar residues become more "soluble" in water at low temperatures (i.e. they move from the more hydrophobic interior of a protein to the more polar outside). Compare the solubility of nonpolar gases like CO2 or N2, which are more soluble at low temperatures. As you heat solutions of nonpolar gases in water, the gases become less soluble as evidenced by bubble formation (i.e. phase separation of dissolved gases as they become more insoluble, as you have observed with a bottle of soda). If protein behavior is governed by this same behavior (greater solubility of nonpolar groups at low temperatures), it would suggest that proteins might denature at low temperatures (leading to increased exposure to water of the nonpolar side chains). This phenomenum has been observed.
c. Protein stability affected by different salt species - Over 100 years ago, Hofmeister determined the effectiveness of different cations and anions of salts to precipitate blood serum proteins in the 0.01 - 1 M concentration ranges. The series is shown below:
Cations: NH4+ > K+ > Na+ > Li+ > Mg2+ > Ca2+ > guanidinium
Anions: SO42- > HPO42- > acetate > citrate > Cl- > NO3- > ClO3- > I- > ClO4- > SCN-
- A salt of pairs of the first ions in these series, for example, (NH4)2SO4, when added to aqueous solutions of proteins, precipitate the native form of the protein. We must account for the fact that it precipitates the protein, and that the protein is precipitated in the native, not denatured state. More on why it precipitates proteins in a moment. The first ion in each series increases the surface tension of water (making it harder to make a cavity in the water to fit the nonpolar molecule). This decreases the solubility of nonpolar molecules. These "salt-out" nonpolar molecules, promoting not dissolution in water but aggregation followed by a phase separation. By analogy, they will stabilize the native state since the buried hydrophobic side chains would have a decreased propensity to move out into the aqueous environment.
- The last ions of the series have less effect on surface tension, and hence increase the solubility of nonpolar molecules ("salt-in"). By analogy, they will destabilize the native state since the buried hydrophobic side chains would have an increased propensity to move out into the aqueous environment.
The Hofmeister Series and its effects on the chemical properties of water and solutes are shown in Figure \(\PageIndex{6}\).
The solubility of benzene in aqueous salt solutions of this series increases from left to right, just as native protein stability decreases from left to right (i.e. the protein's nonpolar core residues become more "soluble" in water, leading to its denaturation).
d. Conservation of hydrophobic core residues - These residues are highly conserved and correlated with structure.
e. Urea denatures proteins - Another additive, urea (H2N(C=O-)NH2), at high concentrations is often used to denature proteins. People used to think that urea competed with the intrachain H bonds and hence unraveled the protein. The arguments above with H bonds dispute this contention since water should then denature protein. How does urea denature proteins? It has been shown that the free energy of transfer of the nonpolar amino acids into 8M urea is increasingly negative as the side chains become bigger and more nonpolar. This is also true for denaturation by guanidine hydrochloride. Both also increase the solubility of nonpolar molecules in a manner proportional to their surface area. The structure of urea and guanidinium, along with the side chains of arginine and the Type II diabetes drug metformin, are shown in Figure \(\PageIndex{7}\).
Figure \(\PageIndex{8}\) shows the free energy of transfer of the nonpolar amino acids into 8 M urea and 6 M guanidine HCl as a function of the surface area of amino acid side chains.
Additives and Their Interactions with Protein Surfaces
Additives to proteins that increase the stability of the folded state of the protein also tend to decrease their solubilities. These additives are excluded from the preferential water hydration sphere around the protein (negative binding of these agents). Denaturants in contrast tend to increase protein solubility and interact preferentially with the protein surface. In their presence, proteins respond by increasing their surface area by denaturation. For stabilizers, proteins try to minimize their surface area by staying "native" and aggregating to form a precipitate, both of which minimize the surface area from which the stabilizing agent is excluded.
The main effect of dissolved ions on water structure has been thought to involve changes in H bonds (either enhancers/structure makers or inhibitors/structure breakers) which correlate with the salting-in or salting-out effects of various ions. Many techniques have been used to study these interactions:
- viscosity: inferential information on the structure
- diffraction (x-rays/neutrons): gives information on the coordination number of solvation shell (static information)
- NMR: information on average relaxation of bulk and hydration sphere water around ions (dynamic information)
- molecular dynamics simulations: which gives insight into short but not long-range interactions between ions and water.
Recent studies have provided conflicting support for the notion of structure makers/breakers. Omta et al. 2003 used femtosecond mid-infrared pump-probe spectroscopy to study actual H-bonds between water molecules in salt solutions (Mg(ClO4)2, NaClO4, and Na2SO4). In pump-probe spectroscopy, a sample is excited with a short pulse (pump) and after a short time lag, with another pulse (probe), which interacts with the excited state. The linear-polarized infrared pulses (pump) were used to excite OH groups in solution, followed by a probe pulse which was polarized 45 degrees compared to the pump pulse. Only those excited OH groups that had rotated in the time interval between the pump and probe would be excited by the probe. Using this technique, the time frame for reorientation of the OH groups, which is related to the "stiffness" of the H bonds, can be determined. The salts had no effect on the rotational motion of bulk water outside of the first hydration shell, which suggests that salts have no effects on the H bond networks in bulk water. Mg2+ ions are considered structure makers, as the ions greatly increase the viscosity of water, brought about supposedly by increased H bonds among water molecules. This study does not support this model. Increased viscosity of Mg solutions must be attributed to those ions directly interacting with water molecules. The solution can be modeled as bulk water with small rigid spheres of ion + first hydration sphere. Clearly, much more experimental and theoretical work must be performed to gain structural insight into the role of salts on water structure. Until then, we will continue to try to understand the effects of different salt on water structure in descriptive terms and with the use of thermodynamic quantities.
Studies have shown that urea binds preferentially to the protein surface, and hence tends to increase the protein's surface area and hydrophobic exposure, and denature proteins. However, note in the figure below, that glycerol, a bigger polar but uncharged molecule, stabilizes the native state. This pair of uncharged additives have correspondingly similar effects on protein stability as do the charged guanidine HCl/ammonium sulfate pair.
Figure \(\PageIndex{9}\) shows how solution additives might interact with the surface of the protein.

Figure \(\PageIndex{10}\) shows a thermodynamic cycle for urea denaturation of proteins
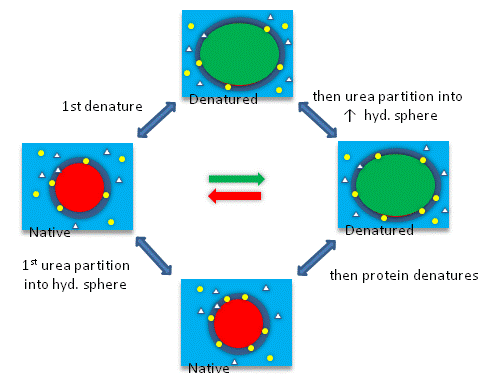
A graphical summary of the types of surface changes that result from protein denaturation is given Figure \(\PageIndex{11}\).
The Hydrophobic Effect and Change in Heat Capacity
Our understanding of hydrophobic interactions has changed dramatically in the last several years. This is not reflected in most textbooks. The hydrophobic effect means different things to different people. Some refer to the transfer of nonpolar solutes/solvents to aqueous solution. Some refer to the same phenomena only if the effects have a unique temperature dependency. Other refer to the ordering of water around nonpolar residues. The most recent explanation centers around the unique temperature dependencies of the transfer reactions. Before we can understand it, here is an interesting bit of data. If you dissolve one mole of methane in hexane, the volume of 1 L of hexane changes 60 ml, but if done in water, the water volume changes 37 ml, indicating that water molecules pack more efficiently around nonpolar molecules than in its absence.
Let's now consider the thermodynamic aspects of the hydrophobic effect, as we did for micelle and bilayer formation. In a brief summary, we found that the free energy of transfer of a hydrocarbon or alcohol from aqueous solution to the pure hydrocarbon or alcohol, for example, was disfavored enthalpically (unexpectedly) but favored entropically (also unexpectedly until we included solvent in our model). These experiments were done at one temperature and gave us our first initial understanding of the hydrophobic effect. We will expand on this view by looking at the enthalpic and entropic contribution to the transfer of benzene into water as a function of temperature. This will lead us to a more modern view of the hydrophobic effect. To do this we have to think about the thermodynamics of mixing two substances with different properties, such as polarity which affects solubility.
If you mix two substances A and B that aren't very soluble in each other, two opposing thermodynamic factors are relevant.
- The tendency to mix is driven by an increase in entropy.
- The mixing is usually opposed by enthalpy.
The later makes "intuitive" sense since you might expect that van der Waal interactions between A-B might be less than those of A-A and B-B (i.e. the old adage "like dissolves like"). If AA and BB self-interactions are stronger, A would not dissolve in B and vice/versa. You would also expect no significant changes in entropy and enthalpy as a function of temperature in this ideal mixing.
The most modern understanding of the hydrophobic interactions involves the mixing of A and B which is characterized by a unique temperature dependency for the value of the change in entropy and enthalpies. At room temperature, if one corrects the entropy changes for effects due just to mixing, the "excess" entropy is what principally opposes taking a nonpolar molecule into water. Enthalpy changes are small. We have modeled this effect using structured water around the nonpolar residues. We will now further our understanding of the hydrophobic effect by using benzene transfer from water as a model system (much as we did with N-methylacetamide for H bonding).
Before we discuss entropy and enthalpy changes accompanying protein folding/unfolding, let's try to learn about the thermodynamic aspects governing benzene solubility in water. What happens to benzene solubility in water and the corresponding thermodynamic parameters as you raise the temperature? The graph in Figure \(\PageIndex{12}\) shows the change in G, H and -TS for taking benzene from pure benzene to water, BB → BW. This is real data. Note that the graph shows -TΔS not just ΔS. When the values of each of these terms, ΔG, ΔH and -TΔS are negative, the transfer of benzene into water is favored. The blue highlighted region shows more values in a more physiologically relevant temperature range (0-1000 C).
Two things to note for right now. ΔG for BB → BW is always positive and hence always disfavored. Another key feature is shown in the vertical dotted line at the temperature at which benzene has its greatest "aversion" to being in water, where the slope of the ΔG vs T curve (dΔG/dT) = 0. At this point, entropy plays no role in the solubility of benzene in water. This goes again the notion of the hydrophobic effect we discussed in Chapter 2.5. This maximum aversion to water is completely driven by enthalpy.
If these axes showed three lines describing the number of ducks, geese and lunes in a lake as a function of lake temperature, no further explanations might be needed. But many years of teaching experience and research shows that thermodynamics parameters are examples of threshold concepts that students struggle with for many years. A graph showing three simultaneously might be uninterpretable to many. So let's deconstruct this graph into a series of stepwise graphs with targeted explanations to facilitate your understanding. These graphs with explanations are shown below.
A graph of ΔG vs T for BB → BW
|
ΔG for BB → BW is positive and hence disfavored over the entire temperature range shown. However note several important features:
|
A graph of ΔH vs T for BB → BW
|
The graph of ΔH vs T for or BB → BW is linear with a positive slope and crosses the T axis at the point indicated by the arrow.
|
A graph of -TΔS vs T for BB → BW
|
The graph of -TΔS vs T for for BB → BW is almost linear with a negative slope which shows that it becomes less entropically disfavored. The curve crosses the T- axis at the point indicated by the arrow.
|
Let's add a bit more to our molecular interpretation of this seemingly anomalous favorable entropy at higher temperatures. As the temperature is raised, the available positional and thermal entropy of water increases significantly. It would seem logical that to then put a nonpolar residue into this system of water would become easier than putting it into more structured water (characterized by fewer microstates and lower positional and thermal entropy) at a lower temperature! (Remember from our review of thermodynamics that If the Tsurr is high, a given heat transfer to or from the surroundings will have a smaller effect on the ΔSsurr. Conversely, if the Tsurr is low, the effect on ΔSsurr will be greater. Atkins, in a recent General Chemistry, uses the analogy of the effect of a sneeze in library compared to one in a crowded street. An American Chemistry General Chemistry text uses the analogy of giving $5 to a friend with $1000 compared to one who has just $10.
But look at the other temperature anomaly. It becomes increasingly difficult from an enthalpic point of view to put benzene in water. At a high temperature, -TΔS becomes zero, and there is no entropic barrier to putting benzene into water. The barrier is completely enthalpic. This is why a more nuanced definition of the hydrophobic effect has emerged.
If you sum ΔH and -TΔS at each temperature, you get the curve shown for the total ΔG to take benzene from pure benzene to water. Notice that it is always positive, so it is always disfavored. The ΔG function is curved. It increases at low temperatures, and decreases at very high temperatures, implying that there will be a temperature at which there is a minimum solubility of benzene in water (a maximum in the positive ΔG). The minimum solubility of benzene (the max. positive ΔG) occurs when dΔG/dT = 0. This occurs when ΔS = 0, and the maximal aversion of benzene to water is completely enthalpic, a statement not in accord with our initial understanding of the hydrophobic effect.
For just PV work, dG = VdP - SdT, so that dG/dT = V dP/dT - S. At the maximum of the curve of G vs T, dG/dT = 0 so
V dP/dT = S. For this system dP/dT = 0 so S = 0. This is observed in the top graph above.
Here is another equation for heat capacity that you derived in physical chemistry:
Cp = dH/dT= TdS/dT.
The last equality stems from Maxwell's relationships, which Physical Chemistry students should remember.
Let's review some more thermodynamics that the physical chemists in the crowd should remember. Even introductory chemistry students should to a degree (a pun). (Molar) heat capacity, Cp, is defined as the heat required to raise the temperature of a mole of a substance 1oC. It has units of kJ (or kcal)/mol. The slope of the enthalpy curve ΔH vs T for BB → BW has units of kJ/mol/K and is the heat capacity, Cp, where Cp = dH/dT.
To refresh your mind and demystify the term heat capacity, let's look at the heat absorbed as ice is converted to gas as a function of temperature (i.e. the phase transition for water). Figure \(\PageIndex{13}\) a graph of the heat absorbed, Qabs/gram vs T (top), and a derivative plot of the top graph (slope of the top graph = heat capacity at each point on the T axis).
We can now learn one final concept from the graphs for benzene transfer into water. The graph of ΔH vs T is linear for the transfer of benzene from the pure liquid into water. We now know that the slope of that graph, ΔCp is a constant positive number for the process when a hydrophobe is exposed to water.
This positive Cp observed when a hydrophobic group is transferred to water, is the signature of our new understanding of the hydrophobic effect.
A positive Cp occurs when both H and S are dependent on temperature, which is observed when a hydrophobe is transferred from a more nonpolar environment to water. Likewise, a negative Cp is observed when hydrophobes in water are transferred to a more nonpolar environment.
Hydrophobic Effect Applied to Proteins
Now let's return to the world of proteins and see how we might apply what we learned from the transfer of benzene from the pure liquid to water. An analogous transfer experiment would be the denaturation of proteins in which buried hydrophobic amino acids are "transferred" to water. Figure \(\PageIndex{14}\) shows the derivative plot of heat absorbed vs T ( i.e a plot of heat capacity Cp vs T) for the thermal denaturation of a protein, obtained using differential scanning calorimetry.
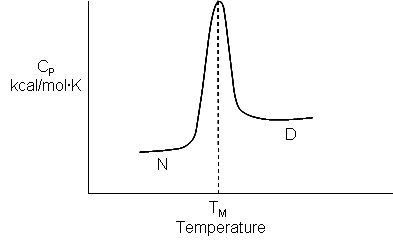
Look at the graph in Figure \(\PageIndex{15}\) which shows the heat capacity of the protein lysozyme at various pHs vs temperature obtained using differential scanning calorimetry.
As the protein is heated, it reaches a temperature at which a large amount of heat is suddenly absorbed, as the protein unfolds. The area under the curve represents the heat absorbed on denaturation (units of cal/g.K x K = cal/g). The temperature at the midpoint is the Tm of the protein. (Why would the Tm be dependent on the pH of the solution?) Notice that there are two ΔCps shown in the graph. One, ΔCd, is associated with the actual denaturation process and is analogous to the change in heat capacity observed in phase changes, such as solid to liquid water. The other is ΔCp which is the difference in heat capacity between the denatured and native state. As was the case for the transfer of benzene to water, the ΔCp for protein denaturation is also positive, suggesting that in protein denaturation, hydrophobes are transferred from the interior of the protein to water.
Figure \(\PageIndex{16}\) attempts to give a molecular description that applies to different regions of the denaturation curve and helps explain the positive ΔCp observed in thermal denaturation curves of proteins.
What is the molecular basis for this large heat capacity change of transfer for benzene. One can show that the Cp is also proportional to the surface area of the nonpolar solute. Figure \(\PageIndex{16}\) shows the smaller, more compact native state, with buried Phe (F) side chains denaturing to the more open D state with exposed F side chains. Since these are nonpolar, we can envision a "clathrate" or cage of ordered water around them. The heat capacity curves for both the native and denatured states are extrapolated into the region where T < Tm (even though there is very little denatured state in that region).
The "caged" water around the exposed F in the D state is low energy due to the "ice-like" H bond network. More heat would be absorbed (as the temperature is increased) to break up that cage compared to the same amount of heat applied to the N state. Hence, Cp D > Cp N. At room temperature, water molecules surrounding the nonpolar residue are low in energy (lots of H bonds) and low in entropy (thermal and positional, fewer available microstates). As the temperature is raised, water populates higher energy states (fewer H bonds) and higher entropy (thermal and positional, more available microstates. The increase in temperature causes "melting" of surrounding water structure in so far as energy and entropy are concerned. The two different energetic states of water provide an energy storage mechanism.
Here is another explanation that might help. Water molecules form "iceberg"-like cage of water around nonpolar molecules, which is often called a clathrate. The water is fully H-bonded (to itself, not to the nonpolar molecule) in a fashion analogous to ice but the geometry of the H bonds is nonideal. This structuring of water decreases its entropy. With increasing temperature, the structured water "melts" which produces the large heat capacity of a solution of a nonpolar molecule in water, just as the actual melting of ice showed a large heat capacity. This large heat capacity is the signature thermodynamic feature of the solution of a nonpolar molecule in water.
For the actual part of the graph in which denaturation occurs (N ↔ D), the following equations can be derived.
\begin{equation}
\begin{gathered}
\mathrm{C}_{\mathrm{p}}=\mathrm{C}_{\mathrm{d}}=\frac{d \mathrm{H}}{d \mathrm{t}} \\
d \mathrm{H}_{\mathrm{d}}=\mathrm{C}_{\mathrm{d}} \mathrm{d} \mathrm{t} \\
\int_{\mathrm{T}_{1}}^{\mathrm{T}_{\mathrm{S}}} \mathrm{d} \mathrm{H}_{\mathrm{d}}=<\Delta \mathrm{H}_{\mathrm{d}}>=\int_{\mathrm{T}_{1}}^{\mathrm{T}_{2}} \mathrm{C}_{\mathrm{d}} \mathrm{d} \mathrm{T}
\end{gathered}
\end{equation}
to help calculate the calorimetric enthalpy changes (ΔHcal = ΔHd) of denaturation from differential scanning calorimetry.
where <ΔHd> is the average enthalpy change that occurs on denaturation which is represented by the blue and red shaded areas in the curve above (between T1 and T2). Compare this to the van 't Hoff enthalpy discussed in Laboratory Determination of ΔGo for Protein Folding/Unfolding.
For the calorimetric determination of ΔCd and ΔHd, the values are temperature dependent, and no assumption about the temperature independence need be made, as in the case of the ΔHvhoff plot.
H2O Clathrate Cages - An ExtensionIs there a more quantitative description of the ordered water than a cage? Sharp et al investigated the "structure" of the caged water around nonpolar and polar molecules in a theoretical analysis supported by molecular dynamics (Monte Carlo) simulations. The average bond angles and lengths of water-water H bonds in the first hydration sphere around a nonpolar molecule like benzene decreased, but increased for polar ones such as potassium ions. The average changes noted arose from two types of H bonds compared to bulk water, those that were shorter and more linear, and those that were longer and more bent. They stated that "nonpolar groups do not so much increase the ordering of water as decrease the disordering". A recent review by Silverstein suggests that an immobile clathrate cage is not a good representation for water surrounding a hydrophobe. Although we like to envision molecular models that allow us to "explain" experimental thermodynamic findings, such models themselves should be subjected to rigorous experimentation. An alternative explanation hinges on water's small size (compared to other solvents), its tight packing and high density. Consider the density of water compared to more nonpolar liquid solvents as seen in the table below. Table: Density of common solvents
Let's consider the density of water surrounding an exposed nonpolar. If we envision the surrounding water as a clathrate, we might assume it is "ice" like. So what are the physical properties of ice and water that might give us insight into the water surrounding a nonpolar molecule? Ice, of course, has a lower density than liquid water. This can't be simply explained by the number of H bonds since experimental evidence shows that ice has an average of 4 H bonds per water molecule compared with liquid water, with an average of 2.4. Experimental data also shows that to accommodate water molecules into a rigid network of interacting waters with tetrahedral symmetry, the H-O-H bond angle increases to 106 from 104.5. Liquid water molecules, with fewer packing constraints, can self-organize to maximize packing and hence macroscopic density. Studies suggest that ten water molecules solvate a buried methyl group and infrared studies show that four of these have significant barriers to rotational diffusion, suggesting they are effectively immobilized and hence "ice-like". Silverstein suggests then that the water surrounding a nonpolar group on the solution should be considered in a dynamic sense with some immobilized (as in ice) and the remaining more fluid-like. |
Now let's review the benzene graph and apply it to protein unfolding one more time. The graph for BB → BW (Figure \(\PageIndex{12}\)) shows a maximum in benzene insolubility. As the temperature is decreased from that maximum, benzene becomes more soluble in water. Alternatively, as temperatures rises to that temperature of maximal insolubility, the solubility of benzene decreases (just like nonpolar gases become increasingly insoluble with increasing temperature). If you extrapolate the ΔG curve in this range of decreasing temperature past the range shown on the graph, it would cross the X-axis and become <0, implying benzene would be favored to dissolve in water. Does the low temperature behavior of benzene/water interactions (becoming more soluble as the temperature is decreased from the maximum temperature for its insolubility) extend to and predict protein behavior at low temperature? Figure \(\PageIndex{17}\) shows the analogy between benzene solubility in water at cold temperatures and cold temperature denaturation of proteins.
In the figure, F stands for a Phe side chain, which can be buried, sequestered from water as it would be in the native state of the protein, and exposed to water, as it might be in the denatured state.) The answer is our question is yes, at low temperatures. The analogy to benzene being more soluble at low temperatures is the hydrophobic side chains in a protein becoming more likely to flip into water, denaturing the protein. The low temperature behavior would predict low temperature protein denaturation. This phenomena has been observed. Note that it doesn't require a change to a state when the nonpolar side chains prefer to be in water, just a change in that direction might be enough to tip the balance and lead to denaturation of the marginally stable protein.
Please note that we are attempting to extrapolate the thermodynamic parameters associated with benzene solubility in water to the denaturation of a protein, NOT TO THE SOLUBILITY OF A PROTEIN IN WATER!
What about high temperature? Proteins denature as the temperature increases in the range that the ΔG curve for benzene reaches a peak. If the buried hydrophobic residues behave like benzene, they would increasingly "prefer" to not flip out into water as the temperature rises to the maximum in the ΔG vs T curve. Hence the benzene predicts that the protein should become more stable. What then explains the observed denaturation of proteins at high temperatures? Another factor must account for it. What is it?
As the temperature is increased, more protein conformational states will become available and occupied. At low temperatures, let's say that there is only one native state available and occupied and (to pick a number), maybe 10 non-native states that are energetically accessible. At high temperatures, there is still only one native state, but perhaps 1000s of accessible nonnative states. More accurately, think of the protein existing in an ensemble of conformations. As the temperature increases, more non-native states can be populated, compared to at lower temperatures, leading to an entropic driving force favoring unfolding. Which way would this chain conformational entropy drive the protein at high temperature? Clearly, it would be driven to the most number of states - to the denatured state. Hence a modern definition of the hydrophobic effect can explain low-temperature denaturation, but not high-temperature denaturation.
Summary of studies from small molecules (N-methyacetamide and benzene)
It is clear that proteins are not all that stable, and many contributions of varying magnitudes must sum to give the proteins marginal stability under physiological conditions. The hydrophobic effect clearly plays a major role in protein stability. Also, since proteins are so highly packed compared to a loser-packed denatured state, collective Van der Waals interactions must also play a significant part. Remember these interactions, especially induced dipole-induced dipole interactions, are short range and become most significant under conditions of closest packing. Opposing folding is the chain conformational entropy just described. Since proteins are so marginally stable, even one unpaired buried ionic side chain, or 1-2 unpaired buried H bond donors and acceptors in the protein may be enough to "unravel" the native structure, leading to the denatured state.
Mutagenesis and Protein Stability
In the last decade, the contributions to the overall stability of a protein from the hydrophobic effect and H bonds have been studied using site-directed mutagenesis. In this technique, the DNA coding sequence for a given amino acid in a gene can be altered so that the new mutant protein differs from the normal (wild-type) protein by one amino acid. To probe the hydrophobic effect, for example, a buried hydrophobic amino acid like Ile could be changed to Gly which is much smaller, and offers a lower hydrophobic contribution to the stability of the native state. The result of this mutation might leave a "hole" in the protein (not unlike the vacant holes in crystal structures of salts). This "hole" might be diminished in size by subtle rearrangement of the protein structure in the vicinity. Certain amino acids would not be used as replacements in such studies. For instance, an Ile would not be replaced with a positively-charge Arg which would clearly destabilize the protein. The extent of destabilization in mutant proteins can be determined by calculating the ΔGo for the native to denatured transition using urea as the denaturing agent as discussed in another section.
Previously, the following statistics were presented concerning the distribution of amino acids in the tertiary structure of a protein. New values are shown below in red, based on much more crystallographic data, as summarized in Pace's article.
- The side chain location varies with polarity. Nonpolar side chains, such as Val, Leu, Ile, Met, and Phe, are nearly always (83%) in the interior of the protein.
- Charged polar side chains are almost invariably on the surface of the protein. (54% - Asp, Glu, His, Arg, Lys are buried away from water, a bit startling!)
- Uncharged polar groups such as Ser, Thr, Asn, Gln, Tyr, and Trp are usually on the surface, but frequently in the interior. If they are inside, they are almost always H bonded (63% buried - Asn, Gln, Ser, Thr, Tyr, again startling) .
- Globular proteins are quite compact, with water excluded. The packing density (Vvdw/Vtot) is about 0.75, which is like the NaCl crystal and equals the closest packing density of 0.74. This compares to organic liquids, whose density is about 0.6-0.7.
Two articles by Pace suggeststhat Dills "influential review (from which much of the above derives) that concluded that hydrophobicity is the dominant force in protein folding" should be rethought. Using site-directed mutagenesis to change Asn (which can H bond through its side chain) to Ala (which can't) in a variety of proteins, he has shown that approximately 80 cal/mol/A3 of stability is gained if a side chain (in this case Asn) can form buried H bonds to buried amide links of the protein backbone. Similar studies of mutants in which Leu is replaced with Ala, and Ile with Val, suggest that only 50 cal/mol/A3 is gained from burying a hydrophobic -CH2- methylene group. Extending these results to protein folding suggests that protein stability is determined more by the formation of buried H bonds than by the hydrophobic effect!
The investigators measured ΔGo for the N ↔ D transition (presumably by varying the urea concentration and extrapolating the ΔGo for unfolding to 0 M urea (see: 4.12: Appendix - Laboratory Determination of the Thermodynamic Parameters for Protein Denaturation). For the reaction as written, ΔGounfolding > 0 at room temperature and 0 M urea. The mutant protein, since they are destabilized, would have a less positive value for ΔGounfolding (They would also have a less negative value for folding since they are less stable). The difference in ΔGounfolding between the wild type and mutant (ΔΔG) is expressed as:
ΔΔG = ΔGounfolding wild-type - ΔGounfolding mutant > 0
ΔΔG > 0 since ΔGounfolding wild-type > ΔGounfolding mutant. The more positive the ΔΔG, the more the mutant is destabilized in comparison to the wild type. The data for a series of mutants is shown below.
Analysis of Mutants: H Bonds in Protein Folding
| mutation | ΔVol side chain (Å3) | % buried | ΔΔG kcal/mol (kJ/mol) (destabilized) |
ΔΔG cal/mol/Å3 (J/mol/Å3) (destabilized) |
| Asn to Ala | 37.4 | 95 | 2.9 (12) | 78 (326) |
| Leu to Ala | 74.5 | 99 | 3.6 (15) | 48 (200) |
| Ile to Val | 25.8 | 100 | 1.3 (5.4) | 50 (209) |
What leads to protein stabilization/destabilization when Asn is changed to Ala?
One possible contributor to stability is the side chain conformational entropy. Since in the mutant, the Ala would find itself in a larger "hole" and have greater freedom for motion, it would have more conformational entropy that would stabilize the mutant over the wild type. Hence this effect can NOT explain the observed destabilization of the Asn to Ala mutant.
In the proteins he studied, only one of eight Asn to Ala mutations involved an Asn in a helix, so the average change could not be attributable to differences in helix propensities for the two amino acids.
In the mutants, assuming no rearrangement of the remaining side chains, there is an "unnecessary" and unoccupied 37 Å3 cavity. The creation of this cavity is thermodynamically unfavorable (about 22 cal/mol/Å3 obtained from values for hydrophobic mutations). If the same penalty were applied here, the Asn to Ala mutant would be destabilized by 0.8 kcal/mol (22 x 37.4), This is significantly less than the observed destabilization (2.9 kcal/mol, 12.1 kJ/mol), so this effect also could not account for the destabilization of the Asn to Ala mutants.
If there were compensatory changes to minimize the cavity size, this would only help to stabilize the protein and hence can not account for the observed destabilization.
Possible Explanation of Destabilization of Asn to Ala Mutants
| possible reasons | explanation | effect on mutant | support observed destab. of mutant? |
| residue conformational entropy | Ala in a bigger hole: more freedom of motion; favored entropically |
stabilize mutant | NO |
|
free energy change |
energy penalty to make an unoccupied cavity approx. 0. 8 kcal/mol (3.3 kJ/mol) |
destabilize | yes but of insufficient size compared to the observed effect (2.9 kcal/mol, 12 kJ/mol) |
| free energy change protein conformational changes |
rearrange protein to fill the cavity | stabilize mutant | NO |
Hence these alternative sources to explain the destabilization of the mutant can't account for the data and we're left with the explanation that the stability of the native protein over the mutant is accounted for by burying the H bond donor and acceptors of the amide group and associated changes in van der Waals interactions.
Pace argues that burying the amide group of Asn is similar to burying the peptide bond of the main chain. Their sizes are very comparable. Free amide groups can form four H bonds, but peptide (amide) groups can only form three. Even if the value of 78 for the ΔΔG (cal/mol/Å3) is adjusted for this, the new value of 62 is still larger than that for burying a methylene group. Analysis of 108 folded proteins has shown that hydrophobic groups contribute 118,200 Å3 of buried volume, compared to 92,000 Å3 for peptide groups. Multiplying these figures by 78 and 49 (from the above table) suggests that overall, burying peptide groups contributes more to protein stability than burying hydrophobic groups.
Would electrostatic interactions of the buried peptide group with the surrounding environment destabilize a protein? Pace argues that this would be more than compensated for by favorable van der Waal's interactions (short range) at the buried site. This can be illustrated by comparing the ΔG transfer of an amide from water to the vapor (11.2 kcal/mol, 47 kJ/mol) compared from water to cyclohexane (7.6 kcal/mol, 32 kJ/mol). Transfer to the vapor is more unfavored (due to the desolvation required when it moves to the gas phase) than to cyclohexane, even though a cavity must be created in the cyclohexane (a process which would be unfavored entropically). Transfer to octanol is even more favored (1.4 kcal/mol, 5.9 kJ/mol) but all these values are still positive (disfavored). Similar experiments with the transfer of a methylene group (-CH2-) are negative, given the hydrophobic effect and the collective close packing van der Waal's interactions possible. These suggest that van der Waals interactions formed on burying an amide in any solvent are stabilizing. Now consider the packing density of atoms for various substances:
Packing Densities
| substance | packing density |
| water | 0.36 |
| cyclohexane | 0.44 |
| closest packed spheres | 0.71 |
| protein interiors | 0.75 |
From this table, it should be apparent that collective van der Waals interactions (short range) will be more stabilizing in the interior of the protein compared to the same groups in bulk water (or in the denatured state). Carbonyl groups are more polarizable than methylene groups, which should contribute to van der Waals interactions.
One other addition. It has been noted that Gly peptides are not very soluble in water. The backbone, even with the polar peptide bonds appears to be solvophobic. If the backbone of any polymer can't interact well with the solvent - i.e. the solvent is "poor" - then the backbone interacts with itself, which drives collapse. If the backbone interacts well with a "good" solvent, it won't collapse as readily.
Protein Stability in Thermophilic Organisms
What kinds of modifications are made to the sequence of a protein as the temperatures at which the organism thrives increase? A recent study by Szilagyi and Zavodszky (Structure, 8, pg 493, 2000) studied 93 structures of 25 proteins, 29 from organisms that live at elevated temperatures (thermophiles, >50oC for optimal growth ) and 64 at nominal temperatures (mesophiles). Here are their results:
- the number of H-bonds and secondary structure elements do not correlate with temperature, but the number of salt bridges do.
- in hyperthermophiiles (>80oC for optimal growth organisms) that thrive at very high temperatures (100oC), few internal cavities were found.
- in those that thrive at intermediate high temperatures (45-80oC), the surface had more polar residues.
- in general, there was an increase in weaker ion pairs (increased distance between the charged side chains) in the hot group, but increases in strong and weak ion-ion bonds in the very hot group.
Kashefi and Lovley recently reported the identification of a bacteria obtained from a hydrothermal vent in the northeastern Pacific ocean. In a laboratory setting, the strain grew in water at a temperature of 121oC under high pressure. These are the same conditions used in autoclaves to produce sterile samples. Cell doubling took place under these conditions in 24 hours. The authors suggest that this strain would be useful to determine molecules and their properties necessary for such high temperature growth.
Using a computational program called Rossetta Design (PNAS, 97, 10383 (2003)), Korkegian et al determined mutations in buried side chains of the homodimer cytosine deaminase. Buried residues are presumably are important in the stability of a protein and are targets for mutagenesis experiments that would increase the melting temperature (Tm) of the protein. In the program, a target sequence was "threaded" onto the sequence of the template protein (the wild-type protein) and changes were made to side chains in the random sequence. Energies were calculated and those changes resulting in lower energies were saved. Target residues (88) within 4 angstroms of the active site and the dimer interface were fixed to those in the wild-type template in order to minimize alterations in the catalytic activity of the enzyme, cytosine deaminase, that they chose to study. Remember, the goal of the study was not to increase the catalytic activity of the enzyme, but rather to increase its themostability. The rest (65) were changed and energies calculated. 49% of the amino acids subjected to random change produced no change in amino acid compared to the template (wild-type) side chain. 16 changes on the surface were ignored. Two sets of changes were observed, one involving amino acids packed between an alpha helix and beta strands, and the other set between two alpha-helices. These later mutants, when prepared in the lab using recombinant DNA technology, were soluble at high protein concentrations, and could be studied. Three different mutants (A23L, I140L, V108I) were made which increased the TM by about 2 degrees. However, a triple mutation had TM values 10 degrees higher than the wild-type protein and a 30-fold longer half life (t1/2) at50 degrees C. When the triple mutant was introduced into bacteria, the bacteria grew better at higher temperatures. Crystal structures of both the wild-type and triple mutants show essentially an identical fold, with about 70 Å2 of additional surface area buried in the mutant protein.
Beeby et al. analyzed sequence and structural data from P. aerophilum (archea) and Thermus thermophilus (thermophilic bacteria) and found that disulfide bonds stabilized proteins from these species. Cytoplasmic protein from eukaryotes don't have disulfides due to the presence of reducing agents (such as glutathione) in the cell. In those thermophiles with disulfides in proteins, a novel protein, protein disulfide oxidoreductase, was found, which catalyzes the formation of sulfide bonds. Finally, Berezovsky and Shakhnovich have also analyzed proteins from hyperthermophilic archaea and bacteria and compared them to analogous proteins from mesophilic bacteria. They found two types of stabilizations of hyperthermophilic proteins, depending on the evolutionary history of the organism. Proteins from cells that originally evolved in high temperature conditions (Archaea) were very compact (maximizing van der Waals interactions, had a high number of contacts per residue, and a high percentage of hydrophobic residues), but did not use specific structural stabilizing interactions (like electrostatic in salt bridges). In contrast, proteins from cells the originally evolved under mesophilic conditions, but later adapted to hyperthermophilic conditions had proteins that evolved specific sequences features that stabilized electrostatic interactions (more charged residues, salt bridges. .



