2.5: Solubility in an aqueous world - The Hydrophobic Effect

Search Fundamentals of Biochemistry

Learning Goals (ChaptGPT o1, 1/25/25)

Below is a series of targeted learning goals designed to help junior and senior biochemistry majors develop a deep understanding of the thermodynamics of solute–solvent interactions and the hydrophobic effect:

• Relate “Like Dissolves Like” to Biomolecular Solubility:

  • Explain why nonpolar molecules (e.g., triacylglycerols, cholesterol esters) are poorly soluble in water and how liquid-liquid extraction exploits these differences.

• Analyze Thermodynamic Contributions to Solubility:

  • Differentiate between enthalpic and entropic factors that contribute to the free energy change (ΔG) for the dissolution or partitioning of biomolecules.
  • Interpret experimental data that show how increasing nonpolar chain length affects ΔG, and discuss the significance of per-methylene free energy changes.

• Apply Free Energy and Chemical Potential Concepts:

  • Use the relationships ΔG = ΔH – TΔS and ΔG° = –RT lnK_eq to explain the spontaneity of solvation and partitioning reactions.
  • Define and relate chemical potential (μ) to free energy changes in a system at equilibrium.

• Understand Partition Coefficients in Biphasic Systems:

  • Describe how the partitioning of a solute between two immiscible phases (e.g., water and octanol) is quantified by the equilibrium partition coefficient (K_part) and how ΔG° can be calculated from experimental measurements.

• Interpret the Hydrophobic Effect:

  • Discuss the entropic penalty associated with forming an ordered water “cage” around a nonpolar molecule, and explain why this drives the aggregation of nonpolar molecules.
  • Analyze how releasing these structured water molecules upon phase separation contributes to a favorable free energy change.

• Integrate Thermodynamic Data with Molecular Behavior:

  • Evaluate experimental thermodynamic parameters (Δμ°, ΔH°, ΔS°) for the transfer of small amphiphiles (e.g., aliphatic alcohols) from their pure liquid to water and rationalize why enthalpic contributions may be favorable while entropy disfavors solubilization.

• Connect Thermodynamics to Biological Function:

  • Relate the principles governing the solubility and partitioning of biomolecules to their roles in biological membranes, drug diffusion across membranes, and overall cellular homeostasis.

These learning goals encourage an integrated understanding of both the quantitative thermodynamics and the qualitative molecular interactions that underlie the hydrophobic effect and solubility in aqueous environments.

Introduction

Many biomolecules, such as triacylglycerols, cholesterol esters, and waxes, are nonpolar. Other biomolecules, like proteins and many lipids, have polar and nonpolar parts. We know from experience that oil floats on the surface of water, showing that it is less dense than water and doesn't dissolve in water. You have also probably performed liquid-liquid extractions in chemistry labs, in which you utilized the solubility properties of nonpolar molecules to extract them from a mixture in water and transfer them to a more nonpolar phase, such as octanol or chloroform. To understand the stability of biomolecules that contain nonpolar parts in aqueous solutions, we need to understand not only the noncovalent interactions of the molecules with water (which we explored in Chapter 2.4) but also the thermodynamics of their molecular interactions in aqueous environments.

We have been taught and internalized the notion that "like-dissolves like." We anthropomorphize molecules to say nonpolar molecules "like" to be in nonpolar environments. We can rationalize solubility properties by examining a molecule's noncovalent attractive and repulsive interactions in an aqueous solution. Still, when we do so, we usually focus on enthalpic contributions to stability. What about entropy? We should consider net changes in noncovalent solute:solute, solute:solvent, and solvent:solvent interactions, as well as their thermodynamic contributions to overall stability. When we consider the thermodynamics of the solubility of molecules in water, we need to determine the ΔG, the free energy change, for all processes involved.

The Change in Free Energy (G) and Chemical Potential (μ)

ΔG, the free energy change for a reaction, determines the spontaneity and extent of a chemical or physical reaction. The free energy of a system depends on 3 variables, temperature T, pressure P, and n, the number of moles of each substance. For the latter, think of solute X on two different sides of a permeable membrane. If the concentration of X is the same on each side, as shown in Figure \(\PageIndex{1}\), the system is in equilibrium.

Figure \(\PageIndex{1}\): A system of a molecule in two compartments separated by a membrane

If the system is composed of two different parts, A and B, the system is at equilibrium (ΔG=0) if T_A = T_B, P_A = P_B, and the change in the absolute free energy per mole of A is ΔG_A/Δn = ΔG_B/Δn. More precisely, using simple calculus, we would discuss incremental changes in absolute free energy/mol, dG_A/dn for A, which is the chemical potential of A, μ_A) and dG_B/dn (μ_B) for B. At equilibrium, dG_A/dn = dG_B/dn. We will use the free energy G here but μ later in this section. G is the absolute free energy/mol (again chemical potential), where G=G^o +RTln[A]. The following equation can be written from the equations you used in introductory chemistry (which we reviewed in Chapter 1.3).

\begin{equation}
\begin{array}{l}
\Delta \mathrm{G}=\Delta \mathrm{G}^{0}+\mathrm{RTIn} \mathrm{Qr} \\
\Delta \mathrm{G}=\Delta \mathrm{H}-\mathrm{T} \Delta \mathrm{S} \\
\Delta \mathrm{G}^{0}=\Delta \mathrm{H}^{0}-\mathrm{T} \Delta \mathrm{S}^{0} \\
\Delta \mathrm{G}^{0}=-\mathrm{RTInK} \mathrm{eq}
\end{array}
\end{equation}

Now, let's apply this to the chemical equation for the solubility of a given solute in water. You eventually reach a saturation point if you add a sparing soluble hydrocarbon (HC) or sodium chloride to water. The salt solution is saturated with dissolved NaCl, and no further increase in NaCl (aq) occurs. The solution reaches saturation for a sparing soluble hydrocarbon, after which phase separation occurs.

Let's add a slightly soluble hydrocarbon liquid (HCL) drop into water, as pictured in the diagram below. At t=0, the system is not at equilibrium, and some of the HC will transfer from the pure liquid to water, so at time t=0, ΔG_TOT < 0. This is illustrated in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): ΔG vs. time for interaction of a hydrocarbon with water

The following equations can be derived.

\begin{equation}
\begin{array}{c}
\Delta \mathrm{G}_{\mathrm{TOT}}=\left(G_{\mathrm{HC}-\mathrm{W}}\right)-\left(G_{\mathrm{HC}-\mathrm{L}}\right)=\mathrm{G}_{\mathrm{HC}-\mathrm{W}}^{0}+R T \ln [\mathrm{HC}]_{\mathrm{W}}-\left(\mathrm{G}_{\mathrm{HC}-\mathrm{L}}^{0}+R T \ln [\mathrm{HC}]_{\mathrm{L}}\right)= \\
\Delta \mathrm{G}_{\mathrm{TOT}}=\left(\mathrm{G}_{\mathrm{HC}-\mathrm{W}}^{0}-\mathrm{G}_{\mathrm{HC}-\mathrm{L}}^{0}\right)+R T \ln \left([\mathrm{HC}]_{\mathrm{W}}-\ln [\mathrm{HC}]_{\mathrm{L}}\right)= \\
\Delta \mathrm{G}_{\mathrm{TOT}}=\Delta \mathrm{G}^{0}+R T \ln \frac{[\mathrm{HC}]_{\mathrm{W}}}{[\mathrm{HC}]_{\mathrm{L}}}
\end{array}
\end{equation}

Now, add a bit more complexity to the last example. Add a hydrocarbon x, to a biphasic system of water and octanol as shown in Figure \(\PageIndex{3}\). Shake it vigorously. At equilibrium, x would have "partitioned" between the two mostly immiscible phases.

Figure \(\PageIndex{3}\): Use of separatory funnel for separating immiscible liquid phases

A simple reaction can be written for this system: X aq ↔ X oct.

If X is a hydrocarbon, ΔG < 0 for the reaction written above. Also, ΔG^o < 0, since this term is independent of concentration and depends only on the intrinsic stability of X in water compared to that of octanol. This simple equation holds:

\begin{equation}
\Delta \mathrm{G}_{\mathrm{TOT}}=\left(\mathrm{G}_{\mathrm{X}-\mathrm{oct}}^{0}-\mathrm{G}_{\mathrm{X}-\mathrm{w}}^{0}\right)+R T \ln \frac{[\mathrm{X}]_{\mathrm{oct}}}{[\mathrm{X}]_{\mathrm{w}}}=\Delta \mathrm{G}^{0}+R T \ln \frac{[\mathrm{X}]_{\mathrm{oct}}}{[\mathrm{X}]_{\mathrm{w}}}
\end{equation}

At equilibrium, ΔG=0 and the equation can be rewritten as:

\begin{equation}
\Delta \mathrm{G}^{0}=-R T \ln \frac{[\mathrm{X}]_{\mathrm{oct}}}{[\mathrm{X}]_{\mathrm{w}}}=-\mathrm{RTlnK}_{\mathrm{part}}
\end{equation}

where K_part is the equilibrium partition coefficient for X in octanol and water. This value can readily be determined in the lab. Just shake a separatory flask with a biphasic system of octanol and water after injecting a bit of X. Then separate the layers and determine the concentration of x in each phase. Plug these numbers into the last equation. You should be able to predict the sign and relative magnitude of ΔG^o since it does not depend on concentration but only on the intrinsic stability of the molecules in the different environments. K_part values are often determined for drugs since they often must diffuse across cell membranes to move into the cytoplasm, where they can act. Drugs, hence, must have a reasonable K_part to pass through the membrane but not so high that they are insoluble.

Introduction to the Hydrophobic Effect

Now let's ask this question: What are the enthalpic and entropic contributions to the ΔG for interacting a nonpolar molecule HC with water? For this section, we will replace ΔG with Δμ (the change in chemical potential, but we will use these terms interchangeably). Likewise, we will use this equation: Δμ^o = ΔH^o - T ΔS^o.

Also, instead of framing the reaction as the dissolution of an organic molecule in water, we will frame it as the transfer of a hydrocarbon X from an aqueous solution to the pure hydrocarbon liquid (HC) or

\begin{equation}
\mathrm{X}(\mathrm{aq}) \leftrightarrow \mathrm{X}(\mathrm{HC})
\end{equation}

Figure \(\PageIndex{4}\) shows the standard free energies of transfer of a hydrocarbon X from an aqueous solution to a pure liquid hydrocarbon (HC), X (aq) ↔ X (HC). where

\begin{equation}
\Delta \mu^{\circ}=\mu^{\circ} x(H C)-\mu^{\circ} x(a q)
\end{equation}

Figure \(\PageIndex{4}\): Standard free energies of transfer (μ⁰) of a hydrocarbon X from aqueous solution to a pure liquid hydrocarbon (HC)

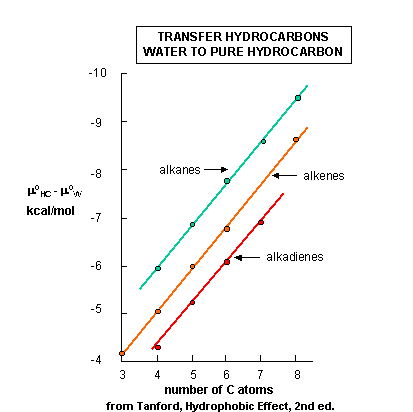
Δμ^o is less than 0 since transfer back to the pure HC is favored from a stability perspective. In each graph, Δμ^o is less than 0, and the value of Δμ^o decreases (gets more negative as you go up the y-axis, which shows increasingly negative values of Δμ^o) in a linear fashion with increasing numbers of carbon atoms in the alkyl chain. Notice the lines are unbelievably straight and parallel. Nature is speaking to us in these figures. By determining the surface area of the hydrocarbon molecules and the decrease in Δμ^o with each added CH₂ (methylene group), one can calculate that the Δμ^o decreases by 25 cal/Ų (105 J/Ų), per methylene added.

We expected that Δμ^o to transfer X to a pure liquid HC would be negative. We could get more information if we could determine both the entropic and enthalpic contributions. Such data is presented in the table below, which shows the transfer of short, single-chain alcohol X (an amphiphile with a polar head and a longer nonpolar "tail") from the pure liquid alcohol (ROH) to water (the opposite of the previous figures.)

\begin{equation}
X(R O H) \leftrightarrow X(W)
\end{equation}

Thermodynamic Parameters for Transfer of Aliphatic Alcohol X from the Pure Liquid to Water at 25^oC (enthalpy determined by calorimetry)

alcohol X	μw^0-μ ROH^0 kcal/mol (kJ/mol)	Hw^0-H ROH^0 kcal/mol (kJ/mol)	Sw^0-S ROH^0 cal/deg mol  (J/deg mol)	(Cp)w^0-(Cp)ROH^0cal/deg mol (J/deg mol)
ethanol	0.760 (3.18)	-2.43 (-10.2)	-10.7 (-44.8)	39 (163)
n-propanol	1.58 (6.61)	-2.42 (-10.2)	-13.4 (-56.1)	56 (234)
n-butanol	2.4 (10)	-2.25 (-9.41)	-15.6 (-65.3)	72 (301)
n-pentanol (solubility 22g/L H2O)	3.22 (13.5)	-1.87 (-7.82)	-17.1 (-71.5)	84 (352)

We expect the Δμ^o to be increasingly positive as the chain length gets longer and their solubilities in water become increasingly disfavored. What is perplexing about this data is not that the transfer of these ROHs to water is disfavored but that transfer is enthalpically favored (negative ΔH⁰). This seems counterintuitive since it goes against the adage that "like dissolves like," as discussed earlier. From an enthalpic point of view, the amphiphiles prefer (albeit marginally) to be in water. What makes this reaction disfavored is entropy. The data shows that the nonpolar molecule would prefer not to be in the water because it is disfavored entropically.

At first glance, you might guess that the entropy should favor the movement of ROHs into the water since they could access a larger volume and have greater freedom of motion. Hence, there are more possible microstates for the ROH in water. However, this is only part of the process. What we haven't considered is the entropy of the water. A literal cavity must be created to accommodate a hydrocarbon in water. The creation of this more ordered cavity must be entropically disfavored (again because the process proceeds to a state with fewer microstates and lower positional entropy).

In the reverse process, transferring the hydrocarbon from water to the pure liquid dissipates the cavity, leading to more available microstates for the released solvent, bulk water. This entropic contribution favors the movement of a hydrocarbon from water to the pure hydrocarbon lipid. This "hydrophobic effect" is the main thermodynamic drive to move organic molecules out of water.

Image this scenario. When you place a hydrocarbon group into water, water seeks (admittedly an anthropomorphic term) to maintain its hydrogen bonding. Hence, it is forced into a more ordered structure around the HC to maintain its H-bonding, characterized by fewer microstates. We will explore the hydrophobic effect in greater detail in a future chapter.

How can we explain the favorable enthalpic contribution of placing a nonpolar molecule into water? Again, this goes against our adage of "like dissolves like". The negative ΔH suggests interactions among all the participants are more favorable when the nonpolar group is in water. One source of such interactions could be the highly structured water in the "cage" surrounding the nonpolar molecule. If it were more structured than bulk water, hence more "ice-like" in nature, then the formation of these extra H-bonds would contribute to the negative enthalpy change. When the nonpolar molecule is removed from the water, which proceeds with a positive ΔH, the "ice-like" water cage would "melt", which, like ice melting, is not favored enthalpically, as heat must be added. Heat energy must be supplied to break the H-bonds as ice changes state to liquid water. This molecular model to understand the thermodynamic data might be simplistic, but for now, let's use it.

Summary

This chapter examines the thermodynamics underlying the solubility of biomolecules in aqueous environments, focusing on understanding how nonpolar and amphiphilic molecules behave in water. It begins by revisiting the principle of "like dissolves like," illustrated by everyday observations such as oil floating on water and the practice of liquid-liquid extraction. These examples highlight that nonpolar substances (e.g., triacylglycerols, cholesterol esters, waxes) do not readily mix with water, while many biomolecules possess polar and nonpolar regions.

The discussion then shifts to a detailed exploration of the thermodynamic factors that govern solubility. Key concepts such as free energy (ΔG), chemical potential (μ), and their dependence on temperature, pressure, and concentration are introduced. The chapter emphasizes that favorable enthalpic interactions and entropic contributions determine the spontaneity of solvation processes. Using the example of transferring a hydrocarbon from water to a pure hydrocarbon liquid, the text derives equations that relate the free energy change (ΔG) to the equilibrium partition coefficient (K_part) through the relation ΔG° = –RT lnK_part.

A significant portion of the chapter is dedicated to the hydrophobic effect. It explains that although the transfer of nonpolar molecules into water might be enthalpically favorable—owing to the formation of structured, “ice-like” water cages around the nonpolar moieties—the overall process is disfavored due to a substantial entropic penalty. This entropy loss arises from ordering water molecules that must occur to accommodate the nonpolar solute. Conversely, when nonpolar molecules aggregate or partition into a nonpolar phase, water is released from this ordered state, resulting in an overall favorable free energy change that drives many biological processes, such as membrane formation and protein folding.

By integrating theoretical thermodynamics with experimental data, this chapter provides a comprehensive framework for understanding how enthalpic and entropic forces interplay to determine the solubility and partitioning behavior of biomolecules, a foundational concept in biochemistry.