17.3B: Principles of Population Growth
- Page ID
- 5831
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Density-Independent Checks on Population Growth
The vagaries of the physical environment, for example drought, freezes, hurricane, floods, and forest fires are often check population growth. Not only may they limit population growth but they often drive existing populations well below their previous level. (And also make it unlikely that many animals will survive long enough to show signs of aging.)
These factors are described as density-independent because they exert their effect irrespective of the size of the population when the catastrophe struck.


Fig.17.3.2.1 Population Density
This graph (from P. T. Boag and P.R. Grant in Science, 214:82, 1981) shows the decline in the population of one of Darwin's finches (Geospiza fortis) on Daphne Major, a tiny (100 acres = 40 hectares) member of the Galapagos Islands. The decline (from 1400 to 200 individuals) occurred because of a severe drought that reduced the quantity of seeds on which this species feeds. The drought ended in 1978, but even with ample food once again available the finch population recovered only slowly.
Catastrophic declines are particularly risky for populations living on islands. The smaller the island, the smaller the population of each species on it, and the greater the risk that a catastrophe will so decimate the population that it becomes extinct. This appears to be one reason for the clear relationship between size of island and the number of different species it contains.
The graph (redrawn from R. H. MacArthur and E. O. Wilson, The Theory of Island Biogeography, Princeton University Press) shows the number of species of reptiles and amphibians on various islands in the West Indies. In general, if one island has 10 times the area of another, it will contain approximately twice the number of species.
The same principle applies to many habitats. In a sense, most habitats are islands. A series of ponds, a range of mountain tops, scattered groves of citrus trees, even individual trees within a grove, all are made up of patches of habitat separated by barriers to the free migration of their inhabitants.
This has practical as well as theoretical importance. As the human population grows, jungles are cleared for agriculture, farms are paved for shopping centers, rivers are dammed for hydroelectric power and irrigation, etc. Although wildlife sanctuaries are being established, they must be made large enough so that they can support populations large enough to survive density-independent checks when they strike.
In 1986, the closing of a dam in Venezuela flooded over a thousand square miles (>2,500 km2) turning hundreds of hilltops into islands. These ranged in size from less than 1 hectare (2.5 acres) to more than 150 hectares (370 acres).
Within 8 years:
- The tiniest islands (<1 hectare) lost 75% of the species that had lived there.
- The larger the island, the fewer species it lost.
- But all the islands - even the largest - lost their top predators; that is carnivores like pumas, jaguars (image), and eagles at the ends of food chains.
- Those animal species that did remain - mostly herbivores and small carnivores - greatly increased their populations because of
- a reduction in competition for resources
- no longer being eaten by predators
Density-Dependent Checks on Population Growth
Intra specific Competition
Intraspecific competition is competition between members of the same species.
In the summer of 1980, much of southern New England was struck by an infestation of the gypsy moth (Porthetria dispar). As the summer wore on,
- the larvae (caterpillars) pupated
- the hatched adults mated
- the females laid masses of eggs (each mass containing several hundred eggs) on virtually every tree in the region
- In early May of 1981, the young caterpillars that hatched from these eggs began feeding and molting.
- The results were dramatic:
- In 72 hours, a 50-ft beech tree or a 25-ft white pine tree would be completely defoliated.
- Large patches of forest began to take on a winter appearance with their skeletons of bare branches.
- In fact the infestation was so heavy that many trees were completely defoliated before the caterpillars could complete their larval development.
- The result: a massive die-off of the animals; very few succeeded in completing metamorphosis.
Here, then, was a dramatic example of how competition among members of one species for a finite resource - in this case, food - caused a sharp drop in population.

The effect was clearly density-dependent. The lower population densities of the previous summer had permitted most of the animals to complete their life cycle. The graph shows a similar population crash; in this case of reindeer on two islands in the Bering Sea. Why the population on St. Paul Island went through so much more severe a boom-and-bust cycle than that on St. George Island is unknown. Many rodent populations (e.g., lemmings in the Arctic) go through such boom-and-bust cycles.
Inter specific Competition
All the ecological requirements of a species constitutes its ecological niche. The dominant requirement is usually food, but others, such as nesting sites and a place in the sun (for plants) may be important as well. When two species share overlapping ecological niches, they may be forced into competition for the resource(s) of that niche. This interspecific competition is another density-dependent check on the growth of one or both populations.

Like so many factors in ecology, interspecific competition is more easily studied in the laboratory than in the field. This graph (based on the work of G. F. Gause) shows the effect of interspecific competition on the population size of two species of paramecia, Paramecium aurelia and Paramecium caudatum.
When either species was cultured alone — with fresh food added regularly — the population grew exponentially at first and then leveled off.
However, when the two species were cultured together, P. caudatum proved to be the weaker competitor. After a brief phase of exponential growth, its population began to decline and ultimately it became extinct. The population of P. aurelia reached a plateau, but so long as P. caudatum remained, this was below the population density it achieved when grown alone.
The habitat of most natural populations is far more complex than a culture vessel. In a natural habitat, the species at a competitive advantage in one part of the habitat might be at a disadvantage in another. In addition, the presence of predators and parasites would limit population growth of the more successful as well as the less successful species. So, in a natural setting, the less effective competitor is usually not driven to extinction.
Character Displacement: an evolutionary response that lessens interspecific competition
When two closely-related species find themselves occupying the same geographic location (sympatric), their requirements for the necessities of life are probably so similar that they are forced into intense interspecific competition. This can lead to one of two possible outcomes.
- The competition may be so intense that one species becomes eliminated entirely; that is, it is driven to extinction there.
- Alternatively, the increased selection pressure may lead to character displacement — the evolutionary divergence of a trait they both use to exploit the resources they both depend on. Such character displacement lessens the competition between them.
Over the past several years, the research teams led by Peter and Rosemary Grant have been able to observe character displacement as it occurred between two species of Darwin's finches. This is their story.
- For many years, G. fortis, the medium ground finch, lived on Daphne Major without its relatives, G. fulginosa, the small ground finch, and G. magnirostris, the large one.
- However, in 1982, G. magnirostris arrived and over the following years grew in population.
- These were good years, with plenty of food, and the two species coexisted nicely.
- However, a severe drought in 2003–2004, sharply reduced the available food including the large seeds that magnirostris and the larger-beaked members of the fortis population competed intensely for.
- The result was a massive die-off of both species with the larger-beaked members of the fortis population suffering greater mortality than the smaller-beaked members of the species.
- The offspring of the fortis survivors, born in 2005, had beaks that averaged over 5% smaller than the average of the parental population. (After the drought of 1977, when G. magnirostris was not on the island to compete with fortis, their beak size increased rather than decreased.)
- This study of character displacement is described in the 14 July 2006 issue of Science.
Reproductive Competition
Declining birth rates also lead to reduced population growth.
We know that humans make deliberate family planning choices, but analogous behavior is found in other animals as well.
- Fruit flies living under crowded conditions lay fewer eggs.
- Laboratory rats in a confined area soon reach a stable population size even though abundant food is available. The main cause is a sharp rise in infant mortality. Reduced maternal care and even cannibalism take a heavy toll of the newborn.
- The honeybee queen regulates her rate of egg laying to the availability of food: reducing it during periods of poor flowering and ceasing entirely in the late summer.
An alternative to limiting the number of offspring per pair of parents is to limit the number of parents. Some mammals and birds achieve this by establishing breeding territories. Each mating pair occupies an area of a size sufficient to supply its needs including those of its offspring. One or both members defend this territory against intrusion from other members of the same species. This behavior not only ensures that the resources on which they depend will not be exceeded but may keep the population in check by preventing breeding among its surplus members.
Social conventions among humans (e.g., attitudes about the proper age of marriage and desirable family size) also have a marked influence on birth rates. However social conventions - and the birth control techniques that may supplement them — have been most successful at reducing birth rates among just those people least in need of it. In the poorer countries, early marriage, a desire for large families, and failure to employ birth control methods reliably are common.
Migration
Migration is often an important density-dependent factor in reducing populations. As the population increases, many of its members emigrate.
Predation

As a population increases, its predators are able to harvest it more easily. These graphs (based on data from Crombie, A. C., Journal of Animal Ecology, 16:44, 1947) show the population changes among flour beetles grown in plain flour (left) and in flour containing pieces of glass tubing.
Each culture was started with four adults of each species. In plain medium, after an initial spurt of both populations, Tribolium continued to expand its numbers while the Oryzaephilus population declined and was eventually driven to extinction (left). Several factors were at work, but predation was by far the most important.
- Tribolium adults feed voraciously on the eggs and pupae of Oryzaephilus.
- But Oryzaephilus adults do not feed so vigorously on Tribolium eggs and do not eat their larvae at all.
Glass tubing provided a refuge for some Oryzaephilus larvae enabling them to complete their life cycle. This reduction in the intensity of predation permitted the two populations to coexist indefinitely (right).
Parasitism
Parasites are able to pass from host to host more easily as the population density of the host increases. For this reason, epidemics among humans are particularly severe in cities. In fact, for most of the period since humans began living in cities, city populations have been maintained only through continual immigration from the countryside. Not until the development of community sanitation, immunization, and other public health measures did cities avoid periodic sharp drops in population as a result of epidemics.
The recurrent epidemics of the "black death" in Europe that began in the fourteenth century caused a sharp decline in population. In just 3 years (1348–1350), at least one-quarter of the population of Europe died from the disease (probably plague). More recently, the great influenza pandemic of 1918–1919 is thought to have killed over 20 million people worldwide.
The house finch, Carpodacus mexicanus, — native to western North America — is a recent immigrant to the eastern United States where it is parasitized by a mycoplasma that reduces the lifespan and fecundity of the birds. Data collected by amateur bird watchers show that the arrival of the disease (in the mid-90s) in areas with a high population of the birds drove their numbers down more than it did in regions of low finch populations. Whatever the starting value, all infected populations ended up with similar populations. This is a clear example of the density-dependent effect of parasitism on a population.
Population Cycles
Some populations go through repeated and regular periods of boom followed by bust.

This graph shows the 10-year cyclical fluctuations in the populations (measured by counting the hides offered for sale at the Hudson Bay trading posts in Canada) of the varying hare ("snowshoe rabbit") and its chief predator, the lynx, from 1850 to 1910. The size of the lynx population was closely dependent on the size of its prey (hare) population. The factors causing the hare population to go through its boom-and-bust cycles are still debated, but predation by lynxes was probably only one factor.
Recent field studies have provided clearer answers for three other cyclical populations, voles (a small rodent) in Finland, the red grouse in Scotland, and lemmings (another small rodent) in Greenland.
Voles
The vole population in Finland regularly goes through 3-year cycles of boom-and-bust. When Korpimäki and Norrdahl removed all their predators (both mammals and birds) from their test areas, the cycles ceased. Here, then, the cycles were driven by the density-dependent check of predation.
Red grouse
The red grouse population in Scotland goes through cycles of 4–8 years. From peak to trough, the population may decline by a factor of 1000. These cycles do not appear to be caused by the hunting of this popular game bird.
The birds are parasitized by a nematode, and infected birds have lower fecundity (birth rates down) and higher mortality (death rates up) than uninfected birds.
P. J. Hudson and his colleagues treated large numbers of birds in several test areas with a drug to prevent or cure an infection. The populations in the treatment areas ceased to cycle. It was not necessary to treat all the birds; 20% of them seem enough to prevent epidemics (just as immunization of humans doesn't have to reach 100% to put an end to pathogen transmission).
Here, then, the cycles were driven by the density-dependent check of parasitism.
Lemmings
A 15-year study of the population of lemmings in northeast Greenland was reported by Gilg, O., et al., in Science, 31 October 2003. These workers showed that the lemming population rises and falls with a cycle of 4 years. The population of the shorttail weasel (aka ermine, stoat), the principal predator of the lemming, does as well but with a 1-year lag behind the lemming population.
Because of this lag, one might expect that the lemming population would continue to outstrip the weasel population until the lemmings bumped into the carrying capacity of their environment (e.g., availability of food and nesting sites). But this does not occur because as the lemming population grows, other predators (e.g., foxes and owls) shift their diet in favor of lemmings.
As the lemming population then begins to decline,
- these flexible predators return to their former food sources while
- the more "picky" weasels decline in numbers as their sole food source, the lemmings, have.
The Carrying Capacity of the Environment (K)

This graph shows the growth of a yeast population in culture. After a period of exponential growth, the size of the population begins to level off and soon reaches a stable value. This type of growth curve is called sigmoid or S-shaped. If we add fresh culture medium to the container, exponential growth resumes until a new, higher plateau is reached. Evidently the growth rate (r) declines as the density of the population approaches a certain limiting value.
When r = 0, dN/dt = 0 and the population ceases to grow. The yeasts have reached zero population growth or ZPG.
The causes:
- running out of food
- accumulation of ethanol. (When its concentration reaches 12–14%, the yeast die (which explains the maximum alcohol content of natural alcoholic beverages like wine).
The limiting value of the population that can be supported in a particular environment is called its carrying capacity and is designated K. When the population is far below K, its growth is exponential, but as the population approaches K, it begins to encounter ever-stronger "environmental resistance". Let us use the expression
K − N
K
as a "growth realization factor", that is, a factor representing the degree to which the population can actually realize its maximum possible rate of increase. Introducing this factor into our original (exponential) growth equation, we get
|
dN = rN dt |
( | K − N K |
) |
The equation tells us that
- If the size of the population (N) is far below the carrying capacity of the environment (K), the growth realization factor will be close to 1, and the population will show exponential growth.
- But as N begins to approach K, the growth realization factor approaches zero, and the rate of population growth drops to zero:
dN = 0 = "ZPG" (zero population growth)
dt

Plotting the growth of a population from an initial growth realization factor of 1 to a final factor of 0 produces a curve like this, called the logistic growth curve or S-shaped curve of growth. Although actual populations are unlikely to follow the theoretical logistic growth curve exactly, the curve can provide us with valuable guidance in managing populations.
Example 1: The logistic curve tells you that you are unlikely to rid your house of a large rat population by setting rat traps. No matter how many you put out, the r for rats is so high (perhaps 0.0147 per day) that they will reproduce faster than you can catch them. What you must do instead is to prevent them from getting food in and around your house. With a sharply-reduced K, their population will decline.
Example 2: The converse of the pest problem is how to keep endangered species from becoming extinct. But outlawing hunting will have no appreciable impact if the habitat on which that species depends for its K — pasture or woods or whatever — disappears under the parking lot of a shopping plaza.
Example 3: Modern intensive fishing methods have repeatedly produced ominous declines in the catch of many species as the populations have been unable to maintain themselves. The logistic curve provides a goal to managing fisheries: harvest at only such a rate that the population is maintained at K/2. At this size, the population is able to grow most rapidly. The value K/2 is known as the maximum sustainable yield.
r -Strategists and K -Strategists
r-strategists
I once plowed up an old field and allowed it to lie fallow. In the first season it grew a large crop of ragweed.
Ragweed is well-adapted to exploiting its environment in a hurry - before competitors can become established. It grows rapidly and produces a huge number of seeds (after releasing its pollen, the bane of many hay fever sufferers). Because ragweed's approach to continued survival is through rapid reproduction, i.e., a high value of r, it is called an r-strategist. Other weeds, many insects, and many rodents are also r-strategists. If fact, if we consider an organism a pest, it is probably an r-strategist.
In general r-strategists share a number of features:
- They are usually found in disturbed and/or transitory habitats. In the second season of my field, perennial grasses and wildflowers had produced a dense carpet of mixed vegetation and not a ragweed plant was to be found.
- They have short life spans. The house mouse, with a maximum life span of 3 years, is an r-strategist.
- They begin breeding early in life.
- They usually have short generation times; that is, they have short gestation periods and are soon ready to produce another crop of young. The housefly can produce 7 generations each year (each of about 120 young).
- They produce large numbers of offspring. The American oyster, releasing a million eggs in one season, is an r-strategist. Most of its offspring will die, but the sheer size of its output increases the likelihood that some offspring will disperse to new habitats.
- They take little care of their offspring, and infant mortality is huge. If we plot a survivorship curve for an r-strategist, it is apt to take the form of the curve labeled D. Although humans are not r-strategists, the higher birth rate in some countries may well be a response to their higher rates of infant mortality (curve B).
- They have efficient means of dispersal to new habitats.
For r-strategists, alleles that enhance any of the traits listed above will be favored by natural selection. Hence, r-strategists are said to be the product of r-selection.
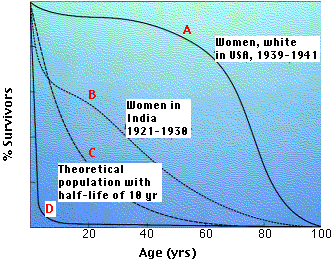
The graph shows 4 representative survivorship curves. The vertical axis gives the fraction of survivors at each age.
- Curve A is characteristic of organisms that have low mortality until late in life when aging takes its toll.
- Cure B is typical of populations in which such factors as starvation and disease obscure the effects of aging, and infant mortality is high.
- Curve C is a theoretical curve for organisms for which the chance of death is equal at all ages. This might be the case for organisms that do not age (some fishes) or those that suffer severe random mortality throughout life (e.g., many songbirds). K-strategists usually have survivorship curves somewhere between A and C.
- Curve D is typical of organisms, oysters for example, that produce huge numbers of offspring accompanied by high rates of infant mortality. Many r-strategists have such a curve.
K-strategists
When a habitat becomes filled with a diverse collection of creatures competing with one another for the necessities of life, the advantage shifts to K-strategists. K-strategists have stable populations that are close to K. There is nothing to be gained from a high r. The species will benefit most by a close adaptation to the conditions of its environment.
Typically, K-strategists share these qualities:
- They are usually found in stable habitats. Most of the species in a mature forest will be K-strategists.
- They have long life spans. The elephant and the tortoise are K-strategists.
- They begin breeding later in life.
- They usually have long generation times. It takes 9 months to produce a human baby.
- Most produce small numbers of offspring. Birds are K-strategists, most species producing fewer than a dozen young each year.
- They take good care of their young. Infant mortality tends to be low. If we plot a survivorship curve for a K-strategist, it usually lies somewhere between curve A (above), where most of the population dies of old age, and curve C, where all ages are equally at risk of being struck down by random hazards.
- K-strategists typically have evolved in such a way that they become increasingly efficient at exploiting an ever-narrower slice of their environment. Thus it is not surprising that many endangered species are K-strategists.
For K-strategists, alleles that enhance their ability to exploit the resources of their habitat; that is, to increase the carrying capacity, K, of their environment, will be favored by natural selection. Hence, K-strategists are said to be the product of K-selection.
Population density can cause shifts in strategy
A team at the Santa Cruz campus of the University of California (Sinervo et al., in the 21 August 2001 issue of Nature) studied the boom-and-bust cycles of the native side-blotched lizard. They found that the lizard population went through 2-year cycles of boom and bust.
Year 1 = Boom
- A low population of adults
- living well below the carrying capacity (K) of their environment
- produced large numbers of young (an r-strategy)
- leading to rapid overcrowding and
Year 2 = Bust
- A large population of adults
- living close to or above the K of their environment
- produced fewer surviving young
- leading to a sharp decline in population and
Year 3 = another Boom year, and so on.
They also found that the population is polymorphic containing:
- females with orange throats that produced as many as 5 clutches of eggs (averaging 6 eggs per clutch) a season. It takes lots of food reserves to make eggs and the eggs of these highly-prolific orange-throated females tended to be smaller — and to hatch into smaller lizards — than those of the
- females with yellow throats. These females tend to lay fewer, but larger, eggs, and the young lizards that hatch from them are larger than those produced by orange-throated mothers.
As they predicted, it turned out that:
- Orange-throated lizards are r-strategists. In boom years, they were more successful than the yellow. The population explosion of young lizards produced by them led to next year's bust.
- Yellow-throated lizards are K-strategists. Producing smaller numbers of larger lizards, they were more successful at leaving surviving offspring to lay the groundwork for the next boom year.
Here, then, intraspecific competition has created a population cycle alternately favoring r-strategists and K-strategists.


