17.3A: The Human Population
- Page ID
- 5830
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Rate of Natural Increase ( r )
Birth rate (b) − death rate (d) = rate of natural increase (r)
- birth rate expressed as number of births per 1000 per year (currently 13 in the U.S.)
- death rate expressed as the number of deaths per 1000 per year (currently 8 in the U.S.)
- So the rate of natural increase is 5 per thousand (0.005 or 0.5%).
Although the value of r is affected by both birth rate and death rate, the recent history of the human population has been affected more by declines in death rates than by increases in birth rates.
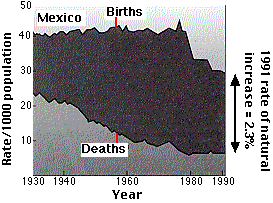
The graph shows birth and death rates in Mexico since 1930. The introduction of public health measures, such as better nutrition, greater access to medical care, improved sanitation, and more widespread immunization has produced a rapid decline in death rates, but until recently there was no corresponding decline in birth rates. In 2012, r is 1.5%. (Data from the Population Reference Bureau.) Although death rates declined in all age groups, the reduction among infants and children had — and will continue to have — the greatest impact on population growth. This is because they will soon be having children of their own. This situation, resulting in a rapid rate of population growth, is characteristic of many of the poorer regions of the world.
The Demographic Transition
Slowly declining birth rates following an earlier sharp decline in death rates are today characteristic of most of the less-developed regions of the world. The shift from high birth and death rates to low birth as well as death rates is called the demographic transition.
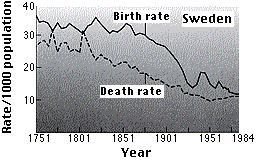
This graph (based on data from the Population Reference Bureau) shows that the demographic transition began much earlier in Sweden than in Mexico and was, in fact, completed by the end of the nineteenth century. The spike in deaths in the interval between 1901 and 1926 was caused by the worldwide influenza pandemic of 1918–1919. The birth rate in Sweden is now (2012) 12/1000; the death rate 10/1000, giving a rate of natural increase (r) of 0.2%.
The Story of Sri Lanka
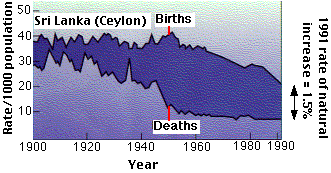
Prior to World War II, advances in public health has been largely limited to affluent, industrialized countries. But since then, improvements in public health have been made in many of the poorer countries of the world - always with dramatic effect on death rates.
- In 1945, the death rate in Sri Lanka (then called Ceylon) was 22/1000.
- In 1946, a large-scale program of mosquito control - using DDT - was started.
- By eliminating its vector, the incidence of malaria dropped sharply.
- After 9 years, the death rate dropped to 10/1000, and by 2012 was 6.
- But a compensating decline in birth rates has come more slowly (18/1000 in 2012).
- So by 2012 the population was increasing at an annual rate of 1.2% (12/1000/year).
- At this rate the population would double in 57.5 years.
Let's see why.
Exponential Growth
The prediction that Sri Lanka will double its population in 57.5 years is based on:
- the assumption that r will remain unchanged (which is surely false)
- the mathematics of exponential growth.
The product of growth grows itself. So the growth of populations is a problem in "compound interest". At the end of each year (or whatever period you choose to use), the base against which the rate is applied has grown. Whatever figures you pick, as long as r is positive, a plot of population as time elapses will produce an exponential growth curve like this one.
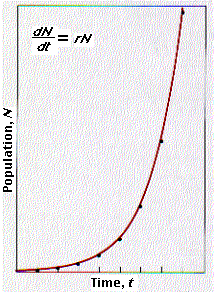
The rate of population growth at any instant is given by the equation
\[\dfrac{dN}{dt} = rN\]
where
- r is the rate of natural increase in
- t — some stated interval of time, and
- N is the number of individuals in the population at a given instant.
The algebraic solution of this differential equation is
\[N = N_0e^{rt} \label{exgr}\]
where
- N0 is the starting population
- N is the population after
- a certain time, t, has elapsed, and
- e is the constant 2.71828... (the base of natural logarithms).
Plotting the results gives this exponential growth curve, so-called because it reflects the growth of a number raised to an exponent (rt).
Doubling Times
When a population has doubled,
\[N = N_0 \times 2.\]
Putting this in our exponential growth equation (Equation \ref{exgr})
\[2N_0 = N_0e^{rt}\]
ert = 2
rt = ln (natural logarithm) of 2 = 0.69
doubling time,
\[t = \dfrac{0.69}{r}\]
So Sri Lanka with an r of 1.2% (0.012) has a doubling time
\[t = \dfrac{0.69}{0.012} = 57.5.\]
(You can use the same equation to calculate how quickly an investment in, for example, a certificate of deposit will enable you to double your money.)
The Population of the World
The solid line in this graph shows estimates of the size of the world's population over the last two millennia. The estimates from 1800 to 1991 are based on more accurate data than those before. The dotted line shows what would happen if exponential growth continued to the year 2100. As you can see, the world's population has been growing exponentially (except during the years of the black death). How long will it continue to do so? (Since the graph was drawn, the world's population has reached 7.1 billion; that is, in 2012 we are still on course.) But can it continue indefinitely? Surely not.

Predicting Future Population Size
With a 2012 rate of natural increase in Mexico of 1.5%, its population would be expected to double in 46 years (0.69/0.015 = 46) from its 116.1 million people now to some 232 million in 2058. Will it? No one knows for certain. What actually happens to population growth depends on a number of factors. Some of these can be estimated with some confidence, some cannot. Two that can are:
- the age structure of the population and
- the total fertility rate (TFR).
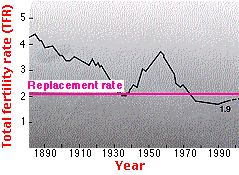
Total Fertility Rate (TFR)
The total fertility rate is the average number of children that each woman will have during her lifetime. The TFR is an average because, of course, some women will have more, some fewer, and some no children at all. Theoretically, when the TFR = 2, each pair of parents just replaces itself. Actually it takes a TFR of 2.1 or 2.2 to replace each generation - this number is called the replacement rate - because some children will die before they grow up to have their own two children. In countries with low life expectancies, the replacement rate is even higher (2.2–3).
Age Structure of Populations
But even a TFR of 2.1 may not ensure zero population growth (ZPG). If at one period a population has an unusually large number of children, they will — as they pass through their childbearing years — increase the r of the population even if their TFR goes no higher than 2.
Most childbearing is done by women between the ages of 15 and 49. So if a population has a large number of young people just entering their reproductive years, the rate of growth of that population is sure to rise.
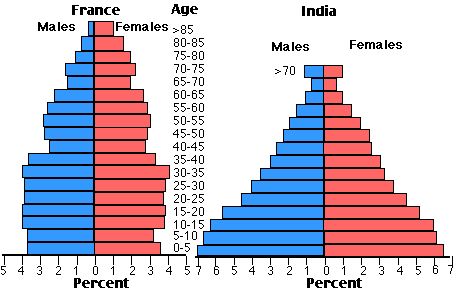
These pyramids compare the age structure of the populations of France and India in 1984. The relative number (%) of males and females is shown in 5-year cohorts. Almost 20% of India's population were children — 15 years or less in age — who had yet to begin reproduction. When the members of a large cohort like this begin reproducing, they add greatly to birth rates. In France, in contrast, each cohort is about the size of the next until close to the top when old age begins to take its toll. Broad-based pyramids like India's are characteristic of populations
- with high birth rates
- low life expectancies (where many people die before reaching old age)
- advances in public health have recently reduced infant and childhood mortality
The age structure of a population also reflects the recent pattern of mortality. In countries where injuries, starvation, and disease, etc. take a heavy toll throughout life, a plot of the age cohorts produces a broad based pyramid like that of India. In France (and other countries in western Europe) almost everyone survives until old age, and a plot of the age cohorts is scarcely a pyramid at all. So even if the TFRs were the same in both countries (they are not - in India it is 2.5, in France, 2.0), India is in for more years of rapid population growth, France is not.
The U.S. Baby Boom
The TFR in the United States declined from more than 4 late in the nineteenth century to less than replacement in the early 1930s. However, when the small numbers of children born in the depression years reached adulthood, they went on a childbearing spree that produced the baby-boom generation. In 1957 more children were born in the United States than ever before (or since). These population pyramids show the baby-boom generation in 1970 and again in 1985 (green ovals).
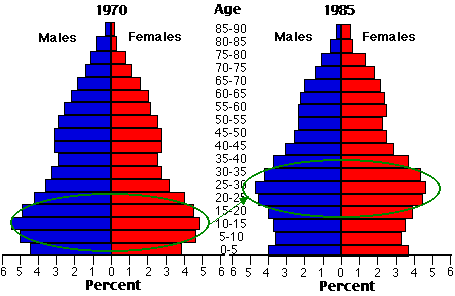
Profound changes (e.g. enrollments in schools and colleges) have occurred — and continue to occur — in U.S. society as this bulge passes into ever-older age brackets. The baby boomers seem not to be headed for the high TFRs of their parents. They are marrying later and having smaller families than their parents. So it looks as though the TFR for the baby-boom generation will not exceed replacement rate. But this is not the same as zero population growth. Even with the current TFR of 1.9, this large cohort of people will keep the U.S. population growing during their reproductive years (current value for r = 0.5%).
Looking Ahead
Exponential growth cannot continue indefinitely. If the current world value for r (1.2%) remains unchanged, the world population would grow from its current 7.1 billion to 9.6 billion over the next 38 years (2050).
- Could the earth's resources sustain such a population?
- If not, how large a human population can live decently on this planet?
Some demographers (students of population) say we have already exceeded the number. Others say the earth can hold billions more.
Whatever the case, there are grounds for some optimism about future population growth.
The world value for r peaked around 1990 and has declined since. This is a reflection of the decline in total fertility rates (TFRs) in undeveloped countries, presumably as the various factors involved in the demographic transition take hold, e.g.,
- improved standard of living
- increased confidence that your children will survive to maturity
- improved status of women
- increased use of birth control measures
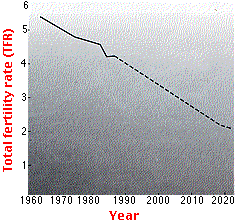
The projection of future TFRs in the upper graph (from the Population Reference Bureau) predicts that the less developed countries of the world will reach replacement fertility around the year 2020. In fact, they will probably reach it sooner because by 2012 the world TFR has dropped to 2.4. Even so, will the world reach zero population growth (ZPG) then?
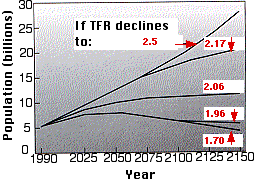
The right graph (based on data from the UN Long-Range World Population Projections, 1991) gives 5 estimates of the growth of the world population from now until 2150, assuming that TFRs decline from the 1991 value of 3.4 to the values shown.
- A value of 2.06 will produce a stable population of about 11.5 billion.
- A value 5% below that (1.96) will cause the population to drop back to close to 6.1 billion while
- a value of only 5% above (2.17) would produce a population of over 20 billion and still rising.
A consensus?
The several agencies that try to predict future population seem to be moving closer to a consensus that the world population will continue to grow until after the middle of this century reaching a peak of some 9.6 billion (up from the current 7.1 billion) and then perhaps declining in the waning years of this century.


