12.11: Estimating Cancer Risks
- Page ID
- 5095
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Is there a safe dose of any mutagen or carcinogen?
We live surrounded by radiation and by chemicals that cause mutations in test organisms (like bacteria, yeast, and mice) and cause an increase in the rate of cancers in experimental animals (rats and mice). Is there any safe dose for humans of these agents (which include oxygen!) The question is exceedingly difficult to answer and, I believe, at low doses, unanswerable. Why?
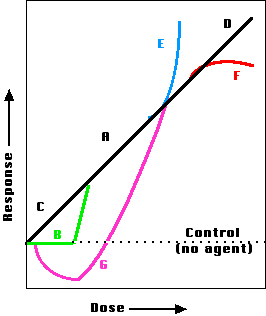
Figure 12.11.1 shows several theoretical dose-response relationships. There is considerable evidence that at moderate doses of a mutagen or carcinogen, the response is linear (A). However, at very low doses of some chemicals, there may be a threshold below which the agent has no effect (B). Many workers believe that for some agents, it is likely that even the tiniest doses will have an effect (C), but the population exposed must be large enough to observe it. This is called the linear no-threshold (LNT) model. Note that even at zero dose, the line does not intercept the origin. This is because even unexposed animals (including people) show a spontaneous level of response (e.g., tumors).
There is also evidence that for some agents in some circumstances, increasing the dose (at relatively low levels) actually reduces the response below control levels (G). This phenomenon is called hormesis. At very high doses, the rate of response may increase faster than the dose (E) as, for example, the probability of a single cell suffering two mutations increases. On the other hand, very high doses may kill off damaged cells before they can develop into tumors (F).
Radiation and cancer
High doses of radiation cause cancer. Various studies, including excellent ones on the survivors of Hiroshima and Nagasaki, show that a population exposed to a dose of 100 millisieverts (mSv) will have a measurable increase (about 1%) in the incidence of cancer. Note that the measurements are made on a population, not on individuals. We can never say that a particular individual exposed to a particular dose of radiation will develop cancer. The induction of cancer is a chance ("stochastic") event unlike the induction of radiation sickness which is completely predictable. The element of chance arises because cancer is an event that occurs in a single cell unlucky enough to suffer damage to several specific genes. However, the energy needed to cause mutations is very low. So if you expose a sufficiently large number of cells to even tiny doses of radiation, some cell is going to be unlucky. How can we evaluate the risk?
Collective Dose
100 mSv causes a 1% increase in cancer in a population; i.e., it should cause an increase of 1 cancer in every 100 people in the exposed population. But if our reasoning is correct, a population of 10,000 people exposed to 1 mSv should also yield one case of radiation-induced cancer. In any population, where the product of radiation dose (in mSv) times population size equals 1 x 104, one case of cancer will be induced. The product of exposure multiplied by the size of the exposed population is known as the collective dose. Its units are (persons)x(mSv).
The population of the U.S. in 2009 was about 305 million. so anything that increases the annual exposure of the U.S. population by as little as 0.01 mSv (a typical chest x ray is 0.02 mSv) per year would cause an additional 305 cases of cancer.
\[ \dfrac{(305 \times 10^6\, persons)(0.01\, mSv)}{1 \times 10^4\, person\, mSv/cancer} = 305 \, cancers\]
But consider:
- The total number of cancer deaths in the United States that year was expected to exceed 560,000.
- How can we possible detect an increase of 305 faced with these large numbers?
Hormesis?
The citizens of Colorado are exposed to background radiation of some 1.8 mSv per year; the figure for Massachusetts is only 1.02 mSv/year.
- If the linear non-threshold model is correct, we would expect to find a higher incidence of cancer in Colorado than in Massachusetts.
- If the background radiation added to other sources keeps both groups below a threshold, then we would expect no difference in cancer incidence.
- If the modest increase in background radiation in Colorado has a protective effect (hormesis), then we would expect that their cancer incidence would be lower than in Massachusetts.
What do we find? In 1999, when adjusted for the age of the population, the incidence of cancer averaged 16% higher in Massachusetts than in Colorado. (If this truly is evidence of hormesis, the mechanism is unknown.)
Some other parts of the world have background radiation levels that dwarf those in Colorado. In some houses in Ramsar, Iran, the inhabitants are exposed to an annual dose of background radiation of as much as 130 mSv per year — over 70 times that in Colorado. Nevertheless, the inhabitants of Ramsar are just as healthy as — or even healthier than — control populations exposed to far lower levels of radiation.
It has been estimated (in this case, using a collective dose value of 5 x 104 person mSv/cancer) that the radioactive fallout from the nuclear accident at Chernobyl (now often spelled "Chornobyl") in 1986 will cause an increase of 17,000 cancers over the lifetime of people living in the Northern Hemisphere.
Large those this estimate seems, it is dwarfed by the 513 million cancer deaths that will occur anyway in this population. Even among those heavily exposed (rescue workers and people living in the region), the expected death toll from cancer is ~4,000 or only 3% more than their death rate from cancer would have been anyway. This is why I say above that the answer to the question of the dangers of low doses of radiation is unknowable.
As of September 2005, some 4000 children and adolescents who drank milk contaminated by the radioactive iodine [131I] released in the accident had come down with thyroid cancer. In their case, the ability of the thyroid gland to concentrate iodine within its cells resulted in those cells receiving a relatively high, not a low, dose. As of that date, however, only 15 of those cancer patients had died.
Chemicals and cancer: dioxin
At one time it was found that the chemical dioxin, which can be produced as a contaminant in the manufacture of paper and cardboard, was leaching from milk cartons into milk itself.
- the concentration in the milk averaged 0.1 part per trillion (ppt) or 0.0001 µg in a liter (109 µg) of milk. Assuming:
- 0.1 µg per day given to rats increases their rate of tumors by 1%
- the idea of collective dose applies to chemicals (that is, a single molecule in an unlucky cell can turn it cancerous)
- people are 100 times more sensitive to dioxin than rats (probably not true) and
- people are 100 times larger than rats
- we conclude that there is a risk of 10 additional cancers in every million people consuming a liter (about a quart) of milk a day from cardboard containers.
And, in fact, this was the estimate made. The uncertainties in such assumptions helps explain the controversy that has so often swirled around the test data on such chemicals as
- the artificial sweeteners cyclamate and saccharin,
- the pesticide Alar,
- the hydrocarbons in a charcoal-broiled steak,
- the chlorinated compounds in municipal water supplies.
Some chemicals appear to have a safety threshold
Cells have a number of different methods for detoxifying certain types of chemicals. So long as these mechanisms are not overwhelmed, they should provide a threshold of safety.


