4.3: Tertiary and Quaternary Structures
- Page ID
- 14936
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tertiary Structure
The tertiary structure of a single chain protein is the overall 3D structure of the protein. A protein of a given primary structure folds to form a 3D structure with embedded secondary structures, super secondary structures and domains. Folded proteins can have a variety of shapes from a roughly spherical or "globular" to a more extended "fibrillar" form. Let's consider the more globular one first. How a protein folds will be discussed in greater detail later, but a more descriptive and simpler view will help us understand the structural features of the folded protein in its tertiary structure.
Start with an unfolded protein. It has a polar backbone with dangling polar charged, polar uncharged, and nonpolar sides attached to the alpha carbon of each amino acid in the primary sequence. On folding, where do these side chains of varying polarity end up? To a first approximation, you may think that a globular protein might fold such that all the hydrophobic amino acid side chains are buried in the interior of the protein, surrounded by other hydrophobic side chains. In a similar fashion, you might expect the polar and charged side chains could be on the surface, exposed to water.
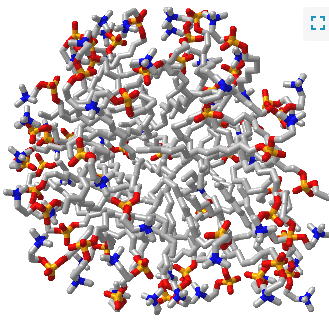
Such a model would be analogous to a micelle, which has an almost "perfect" separation of polar (on the surface) and nonpolar atoms (buried). Figure \(\PageIndex{1}\) shows an interactive iCn3D model of a micelle below, which consists of 54 self-associated molecules of dodecylphosphocholine fatty acids.
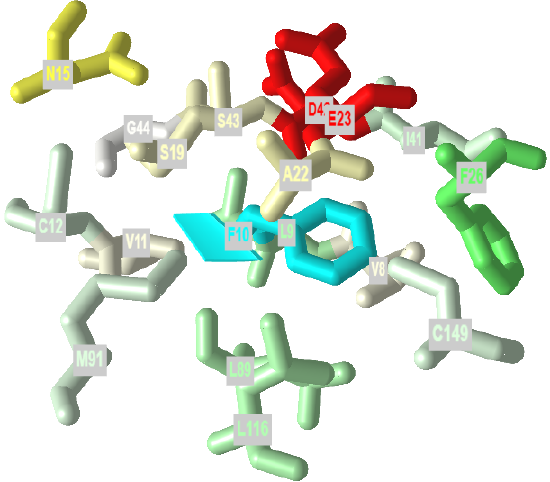
If protein folding was only that simple! Topologically, it is impossible for a protein to fold in an intramolecular fashion in a strict analogy to the intermolecular aggregation of single chain amphiphiles into a micelle. Consider also that the entire backbone is polar! To a first approximation we would expect the bulk of nonpolar groups would be buried, surrounded by other nonpolar groups. Likewise, we would expect the bulk of polar and charged groups would be on the surface. Figure \(\PageIndex{2}\) shows an interactive iCn3D model of part of human low molecular weight protein tyrosyl phosphatase (1xww). It shows one buried nonpolar side chain (Phe 10) surrounded by essentially all nonpolar side chains of other amino acids.
Figure \(\PageIndex{2}\): A buried phenylalanine in low molecular weight protein tyrosyl phosphatase (1xww) (Copyright; author via source).
Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...LC53qmf4FyszT7
The completely nonpolar Phe 10 side chain is shown in cyan. The atoms with 5 Angstroms are color-coded using the Wimley–White whole residue hydrophobicity scale, which uses not only side chain but peptide bond contributions that are determined experimentally by determining free energy of transfers of groups to nonpolar environments. The color scale runs from cyan (nonpolar) to red (polar/charged. Like a micelle, the protein is roughly spherical.
Noncovalent interactions between atoms within a protein chain help drive protein folding. The noncovalent interactions (also termed intermolecular forces in traditional introductory chemistry classes, include ion-ion, ion-dipole, hydrogen bonds, dipole-dipole, induced dipole - induced dipole (often called London Dispersion Forces) and variants including ion-induced dipole, etc. We generally use the same terms when describing these interactions within and between proteins. Ion-Ion interactions are usually called salt bridges, and induced dipole-induced dipole are often called hydrophobic interactions.
Let's look at some specific interactions with a given protein chain (the light chain of the mouse immunoglobulin G, PDB 1D = 4hdi). Manipulate the iCn3D model in the exercises below and answer the following questions. Use your mouse to hover over amino acids to help in identification.
Exercise \(\PageIndex{1}\)
Name the types of interactions between the following side chains in the iCn3D image above. A large images can see by using this link: https://structure.ncbi.nlm.nih.gov/icn3d/share.html?DrdnVubujRaihTcr9
a. Leu 52 and Ile 53, Val 63, Phe 67 and Leu 78
b. Arg 24 and Asp 75
c. Asp 170 and Lys 108
d. Tyr 178 and Lys 147
e. Glu 190 and Arg 160
f. Tyr 191 and Phe 214
- Answer
-
Add texts here. Do not delete this text first. a
a. hydrophobic interactions, induced dipole-induced dipole
b. salt bridge, ion-ion
c. salt bridge, ion-ion
d. pi-cation
e. salt bridge, ion-ion
f. Aromatic-aromatic, induced dipole-induced dipole
You can analyze the noncovalent interactions within and between a protein using PIC- protein interactions calculator
In the next exercise, identify the likely hydrogen donors and acceptors in the pairs shown
Exercise \(\PageIndex{1}\)
Are these hydrogen bonds
- side chain to side chain?
- main chain to main chain?
- side chain to main chain?
a. Ile 111: Gln 171
b. Gln 6: Thr 107
c. Ile 53: Trp 40
d. Try 37:Thr 97
- Answer
-
a. Ile 111: Gln 171 - side chain to side chain
b. Gln 6: Thr 107 - side chain to side chain
c Ile 53: Trp 40 - main chain to main chain
d. Try 37:Thr 97 - main chain to main chain
A more realistic understanding of noncovalent interactions
But are all the nonpolar side chains buried? How about the polar uncharged and polar charged side chains? What are the preferred dispositions of side chains in proteins as derived from the crystal structure of thousands of proteins? Here are some conclusions from a paper by Pace (Biochemistry. 40, pg 310 (2001).
- On average, about 50% of the amino acids are in secondary structures. On average, there is about 27% alpha helix, and 23% beta structure. Of course, some proteins are almost all alpha-helical, and some are almost all beta structure, but most are a mixture.
- The side chain location varies with polarity. Nonpolar side chains, such as Val, Leu, Ile, Met, and Phe are predominately (83%) in the interior of the protein.
- Charged polar side chains are almost equally partitioned between being buried or exposed on the surface. (54% - Asp, Glu, His, Arg, Lys are buried away from water, a bit startling!)
- Uncharged polar groups such as Asn, Gln, Ser, Thr, Tyr are mostly (63%) buried, and not on the surface (a bit startling).
- Globular proteins are quite compact, with water excluded. The packing density (Volvdw/Voltot) is about 0.75, which is like the NaCl crystal and equals the closest packing density of 0.74. This compares to organic liquids, whose density is about 0.6-0.7.
Tertiary structure and pKa Values
If a charged side chain is buried in a protein, you would expect that it would be surrounded, in general, by either oppositely charged side chains, to which it could form an internal salt bridge (ion-ion interaction), or a polar uncharged group with which it could interact through dipole-dipole or, more specifically, H bond interactions. You would also expect that if it were not near an oppositely charged side chain, that it would exist, if buried, in an uncharged state.
Hence the pKa of side chains would be dramatically affected by the nature of its microenvironment (as we have already seen with the pKa of acetic acid in solvents of different polarity). NMR spectroscopy has been used to determine the pKa values of specific side chains in proteins whose crystal structure is known. Pace et al (2009) summarize data on the properties of ionizable side chains in a series of proteins whose structure has been determined. The intrinsic pKa, pKaint or prototypical pKa value for a side chain exposed to water can be determined using a pentapeptide containing the target amino acid X surrounded by 2 Ala on either each side with both the N and C termini of the peptide blocked so they are uncharged. Table \(\PageIndex{1}\) below shows the pKa values of ionizable side chains in a series of proteins compared to that in the control pentapeptide.
| Group | Content % | Buried % | pKa int in AAXAA | pKa avg | low pKa | high pKa | # measurements |
|---|---|---|---|---|---|---|---|
| Asp | 5.2 | 56 | 3.9 | 3.5 + 1.2 | 0.5 | 9.2 | 139 |
| Glu | 6.5 | 48 | 4.3 | 4.2 + 0.9 | 2.1 | 8.8 | 153 |
| His | 2.2 | 72 | 6.5 | 6.6 + 1.0 | 2.4 | 9.2 | 131 |
| Cys | 1.2 | 90 | 8.6 | 6.8 + 2.7 | 2.5 | 11.1 | 25 |
| Tyr | 3.2 | 67 | 9.8 | 10.3 + 1.2 | 6.1 | 12.1 | 20 |
| Lys | 5.9 | 34 | 10.4 | 10.5 + 1.1 | 5.7 | 12.1 | 35 |
| Arg | 5.1 | 56 | 12.3 | ||||
| C term | 3.7 | 3.3 + 0.8 | 2.4 | 5.9 | 22 | ||
| N term | 8.0 | 7.7 + 0.5 | 6.8 | 9.1 | 16 |
Table \(\PageIndex{1}\): pKa values of side chains in actual proteins
A quick glance a the table shows a huge variation in the pKas of ionizable side chains in proteins with the pKa of Asp varying over a range of 8.7 pH units, showing that it can act at physiological pH as either a strong acid or a moderate base. Three majors effects can perturb the pKa of ionizable side chains:
1. Dehydration of the side chain as it is buried in a protein (Born Effect): The stability of a charged group depends on the polarity of the medium in which it exists. Ions are more stable in water than in nonpolar solvents as the water molecules can reorient and interact with the ion through ion-dipole or ion-H bond interactions, which effectively shields the ion from other counter ions. The shielding effect of water is related to the dielectric constant, ε, of the solvent. Coulomb's law can be written as:
\[\mathrm{F}=\frac{\mathrm{k} \mathrm{Q}_{1} \mathrm{Q}_{2}}{\mathrm{r}^{2}}=\frac{\mathrm{Q}_{1} \mathrm{Q}_{2}}{4 \pi \varepsilon \mathrm{r}^{2}} \nonumber \]
Epsilon is the dielectric constant of the solvent. Water has a higher dielectric constant (80) than nonpolar solvents (4-10) and shields opposing charges more, stabilizing them. Hence the pKa of side chains of those amino acids whose deprotonated states are charged will have their pKa values raised (so they are less acidic) in nonpolar environments. The reverse holds for side chains whose protonated form is charged. Pace cites as an example two mutants of staphylococcal nuclease in which a buried Val 66 is changed either to Asp or Lys. The buried Asp has a pKa of 8.9 compared to 5.5 for the buried Lys. These changes were not compensated for with new charge-charge interactions, so the change can be attributed to the dehydration (or Born) effect.
2. Ion-Ion interactions with another charged side chain through Coulombic forces: This effect can be most readily observed at the surface of the protein. Pace cites a study of RNase S that is devoid of Lys and has a pI of 3.5. Five Asp and Glu were replaced on the surface using site-specific mutagenesis with Lys, which changed the pI of the protein to 10.2. At pH 7, the protein without Lys had a charge of -7 while the protein with 5 Lys had a charge of +3. The crystal structures were similar so Coulombic interactions would determine the differences in the pKa of the 11 common side chains. On average the mutant pKas were higher by 0.75 pH units, which makes sense as the mutant had a high pI. Calculated pKa values were similar to those determined by NMR. These data are consistent with the idea that Coulombic interactions are the chief cause of pKa changes in surface side chains.
3. Charge-dipole interactions and H bonds: It should be obvious that charge states of ionizable side chains would be adjusted to optimize H bond (and more generally charge-dipole) interactions in proteins. If the interactions are optimal in the charged state, pKa values for His and Lys would be increased and for Asp, Glu, Cys, and Tyr they would be decreased. Pace cites the buried Asp 76 in RNase T1 in which the Asp is charged but does not form an internal salt bridge. It has a depressed pKa of 0.6 and has 3 H bonds to the side chains of Asn 9, Tyr 11 and Thr 91. Mutants were made to remove the H bonds to see the effect on the pKa of Asp 76. Removing 1, 2, or 3 H bonds changed the pKa to 3.3, 5.1, and 6.4 respectively. The 6.4 value is much higher than the pKint, which can be attributed to the Born effect.
Quaternary Structure
Primary structure is the linear sequence of the protein. Secondary structure is the repetitive structure formed from H-bonds among backbone amide H and carbonyl O atoms. Tertiary structure is the overall 3D structure of the protein. Quaternary structure is the overall structure that arises when separate protein chains aggregate with self to form homodimers, homotrimers, or homopolymers OR aggregate with different proteins to form heteropolymers. Most protein subunits in a larger protein displaying quaternary structure are held together by noncovalent interactions (intermolecular forces), although in some, they are also held together by disulfide bonds (an example includes immunoglobulins).
Figure \(\PageIndex{3}\) shows an interactive iCn3D model of a homodimer, the variable domain of the T cell receptor delta chain (1tvd). Carefully rotate the model to see the two identical chains held together by noncovalent interactions
Figure \(\PageIndex{3}\): variable domain of the T cell receptor delta chain (1tvd) (Copyright; author via source).
Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...yN6B43P7tvHcR7
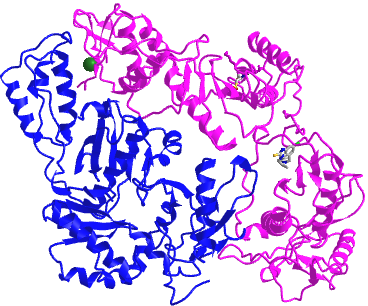
Figure \(\PageIndex{4}\) shows an interactive iCn3D model of a heterodimer, reverse transcriptase (1rev). Carefully rotate the model to see the two identical chains held together by noncovalent interactions
Figure \(\PageIndex{4}\): variable domain of the T cell receptor delta chain (1tvd) (Copyright; author via source).
Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...2mmkgdR9Z2dTQ6
Macromolecule Oligomer Formation and Symmetry
Many proteins are found in aggregated states and hence have quaternary structure. Hemoglobin consists of two alpha and two beta monomers (or protomers) which assemble to produce the biologically relevant heterotetrameric protein. A given monomer can self-aggregate to form homooligomers such as dimers (M2), trimers (M3), tetramers(M4), or or higher oligomers (Mn). The oliogomers often display symmetry with respect to the geometric arrangement of the subunits. Symmetry is an important component of the many kinetic models for catalysis.
Most oligomeric proteins contain protomers that are symmetrically arranged. What mechanism determines whether a monomeric protein forms a homooligomer? Why do they stop at a certain n value? Can proteins be engineered to do so? If mutation can induce oligomer formation, then fewer mutations would be required to produce a symmetric oligomer from subunits since fewer mutations would be required. Why? A single mutation in a single monomer would be represented n times in a single oligomer of n monomers. This fact probably underlies the reason that oligomers display exquisite symmetry. Hence a basic knowledge of the symmetry of protein oligomers is necessary.
In the study of small molecules, chemists describe symmetry through the use of mathematical symmetry operations and elements, which find great use in analysis of structure and in molecular spectroscopy. These concepts are usually first encountered in physical and inorganic chemistry classes. They are a bit complicated so we will offer a limited introduction.
A symmetry operation is a movement of an object like a molecule that leads to an identical, superimposable molecule. Each operation has a symmetry element (point, line, or plane) about which the motion occurs. Some examples are shown in Table \(\PageIndex{2}\) below:
| Element (with Jmol link) | Operation |
| inversion center (i) | projection through center (point) of symmetry of point x,y,z to point -x,-y,-z |
| proper rotation axis (Cn) | rotation around a Cn axis by 360o/n where C denotes Cyclic |
| horizontal (σh) and vertical (σv) symmetry plane (reflection) | reflection across a horizontal (h) or vertical (v)plane |
| improper rotation axis (Sn) | rotation around a Sn axis by 360o/n followed by reflection in plane perpendicular to the axis. |
Table \(\PageIndex{2}\): Symmetry Elements and Operations
Luckily for students trying to apply these rules to protein oligomers, biomolecules made up of chiral monomers containing L-amino acids, can not be converted to identical structures using inversion or reflection since the chirality of the monomer would change. For proteins, this would entail an L to D amino acid change. That excludes all but proper rotation axes (Cn) from the list above.
A point group is a collection of symmetry operations that define the symmetry about a point. The 4 types of symmetries around a point are those described above: rotational symmetry, inversion symmetry, mirror symmetry, and improper rotation. We'll just consider two versions of rotational symmetry.
Cyclic (Cn) - Single Cn rotation axis.
These are very common in proteins that form dimers, trimers, tetramers, etc of identical monomers. These are called homo n-mers. In this point group note that the n in Cn is equal to the number of monomers and the angle of rotation is 360o/n. Figure \(\PageIndex{5}\), adapted from Voet and Voet, shows a cartoon model for C2 symmetry.
Here are some protein examples with Cn symmetry with the symmetry axis shown as a red vertical line.
|
Symmetry/ homo n-mer |
click for popup model |
|
C2: homo 2-mer |
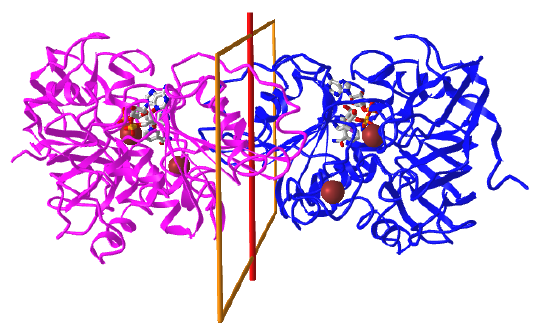 |
|
C3: homo 3-mer |
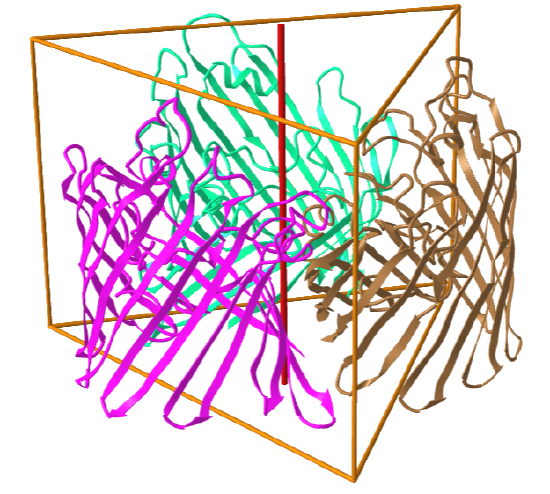 |
|
C4: homo 4-mer |
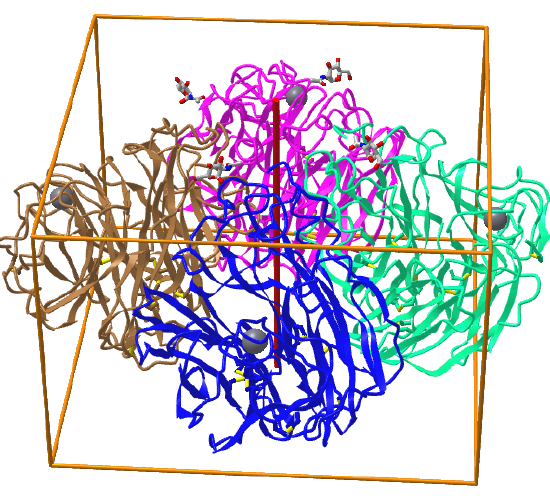 |
Symmetric complexes can also have empty interior volumes designed for specific function. Take for example, the human mitochondrial Hsp60-Hsp10 chaperonin complex (6MRD), which assists in protein folding in the mitochondria. It is a hetero 14-mer (A7B7) and displays C7 symmetry, as shown in Figure \(\PageIndex{6}\), an interactive iCn3D model below. The cyan surface is from 7 A monomers while the red is from 7 B monomers
Figure \(\PageIndex{6}\): Hsp60-Hsp10 chaperonin complex (6MRD) with C7 symmetry (Copyright; author via source).
Click the image for a popup (long load) or use this external link:(long load) https://structure.ncbi.nlm.nih.gov/i...jEEY5tu19nXcp6
Dihedral (Dn) - Mutually perpendicular rotation axes.
These display higher symmetry as they contain (a) C2 axis(es) perpendicular to a single Cn axis. The minimal number of subunits is n. Most protein oligomers fall into this category. The packing (or asymmetric) unit does not have to be a single monomer but could be a heterodimer. Dn symmetries are more difficult to see but structures in the PDB conveniently provide the type of global symmetry and stoichiometry when symmetry is present.
A D2 point group has 1 C2 axis and 2 perpendicular C2 axes, and 4 monomers (like Hb). These proteins can dissociate into two dimers (such as two α/β dimers for Hb). Note that a different arrangement of 4 monomers could produce an oligomer with C4 symmetry instead of D2. Also note the hemoglobin, a tetramer (α2β2) displays pseudo D2 symmetry since the α and β subunits are slightly different in sequence but their folds are almost identical. It also displays C2 symmetry.
Figure \(\PageIndex{7}\), adapted from Voet and Voet, shows a cartoon model for D2 symmetry.
A D4 point group has 1 C4 axis and 4 C2 axes, along with 2n=8 subunits. An example of a D4 point group is ribulose bisphosphate carboxylase/oxygenase (RuBisCO) which has 8 subunits (where a subunit, or more technically the asymmetric subunit, is a dimer of a small and large molecular weight protein). This point group could arise from quaternary structure of two C4 tetramers or four C2 dimers.
Here are some homo n-mer protein examples with Dn symmetry.
|
Symmetry/ homo n-mer |
click for popup model |
|
D2: homo 4-mer |
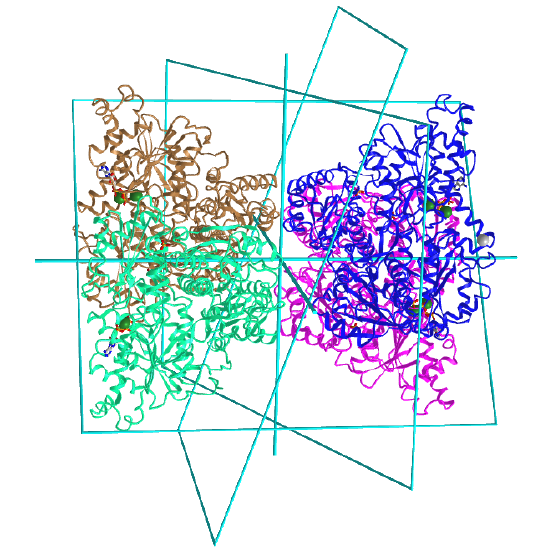 |
|
D3: hetero 12-mer A6B6 |
 |
| D5: homo 10-mer glutamine synthetase (2OJW) |
 |
Cubic Groups
Now let's consider some cases in which a large number of rotation axes exist that fit the symmetry of simple geometric shapes called the Platonic solids, in which all faces, edges and angles are congruent. The five Platonic shapes, described by Plato, are shown inscribed in spheres in Figure \(\PageIndex{8}\):
These can also be inscribed in cubes. A tetrahedron and octahedron (actually the overlap of 2 tetrahedron) are shown inscribed in a cube in Figure \(\PageIndex{9}\).
Since all of the Platonic solids can be inscribed in a cube, they all have basic cubic symmetry. Cubes have a total of 13 symmetry axes: three C4 axes passing through the centers of opposite faces, four C3 axes passing through opposite vertices (diagonals), and six C2 axes passing through the centers of opposite edges. The other Platonic solids have related C3 axes (diagonals connecting opposite corners for cubes, diagonals from a vertex to the opposite face for tetrahedrons, lines connecting two opposite faces for octahedron, etc ) but they all can be considered to be part of the cubic point group. The rotation axes for each of the Platonic solids are shown in Table \(\PageIndex{3}\)below.
| # and type rotation axes | # monomers/asymmetric units | Shape |
| 3 C2, 4 C3 | 12 | tetrahedron |
| 6 C2, 4 C3, 3 C4 | 24 | cube/octahedron |
| 15 C2, 10 C3, 6 C5 | 60 | dodecahedron/icosahedron |
Table \(\PageIndex{3}\): Cn axes and number of monomers in Platonic solids symmetries
We'll consider examples of tetrahedral, octahedral and icosahedral symmetries, which depend on the overall shape and number of monomers in the functional structure. In some cases, the symmetry of the packed monomers is not perfect. This applies to monomers in clathrin since the monomers can form different structures) and hemoglobin (in which the four subunits are very similar (alpha and beta) but not identical, as described above.
When many monomers form oligomers, it seems that homomers are favored evolutionarily over heteromers. One explanation for this is that in symmetrical arrangements of monomers, there are fewer unique subunit-subunit interfaces that have evolved for complementary of fitness of shape and noncovalent interactions than for heteromers. The same argument applies to the formation of symmetric vs asymmetric arrangements of homo n-mers.
A final note: The words tetrahedron, cube, octahedron, dodecahedron and isocahedron refer to the shape of structures. The words tetrahedral, cubic, octahedral, dodecahedral and isocahedral should be reserved for the type of symmetry. This can be a great source of confusion. Take the case of the E2p, dihydrolipoyl acyltransferase. The homo 24-mer version (from Azotobacter vinelandii, 1DPB) has the shape of a cube with octahedral symmetry, while the homo 60-mer (from Bacillus stearothermophilus, 1B5S) has the shape of a dodecahedron with the icosahedral symmetry.
It is sometimes difficult to determine the actual biological structure and its symmetry from crystal structure given the artificial packing of the protein in the crystal state. Also, other than for icosohedral virus assemblies, there aren't that many examples of proteins that show tetrahedral, octahedral and dodecahedral symmetries. No structure in the Protein Data Bank is listed with a global symmetry of cubic. We'll describe a few structures with tetrahedral, octahedral and icosohedral global symmetries, knowing that they all fall in the cubic point group.
Tetrahedral - 4 sided
A tetrahedron has four C3 axes - diagonals from a four corners/vertices to the opposite faces as well as three C2 axes, which are the same as for the cube (since a tetrahedron can be inscribed inside a cube).
| Protein (pdb) |
Symmetry/Homo X-mer |
Structure - subunits | Symmetry |
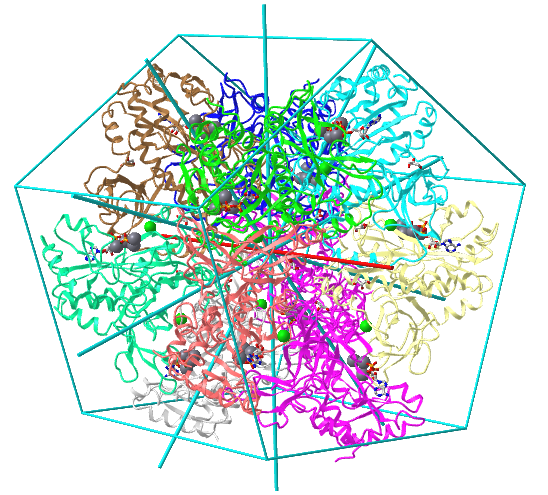
| L-aspartate beta-decarboxylase (2zy2) | tetrahedral/homo 12-mer | 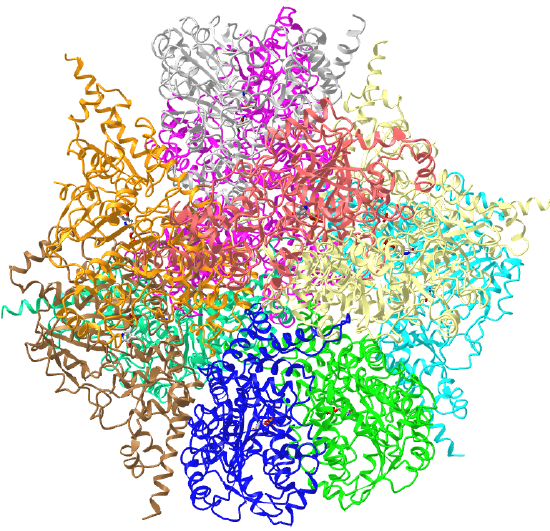 |
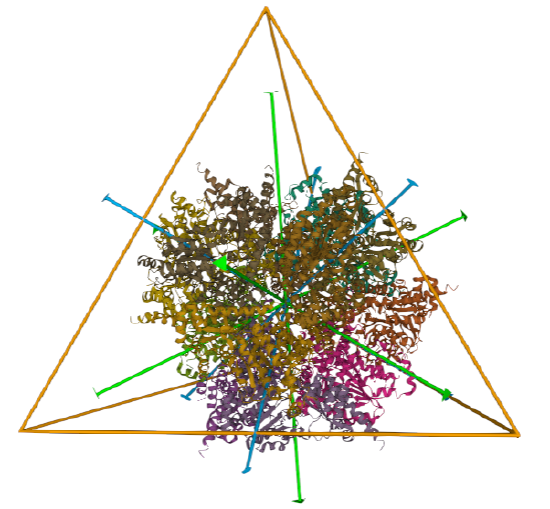 |
| ornithine carbamoyltransferase (1A1S) | tetrahedral, homo 12-mer | 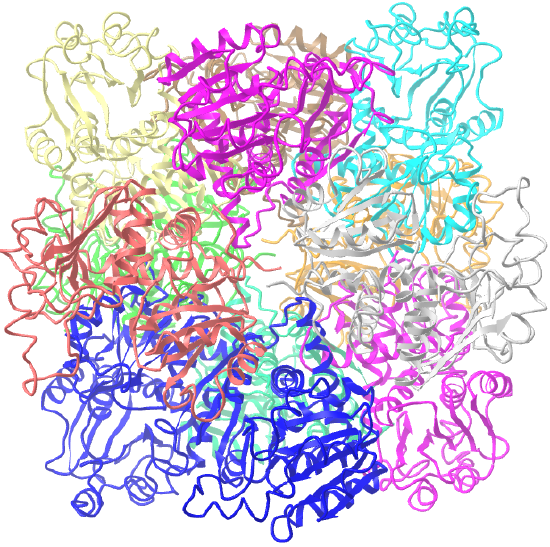 |
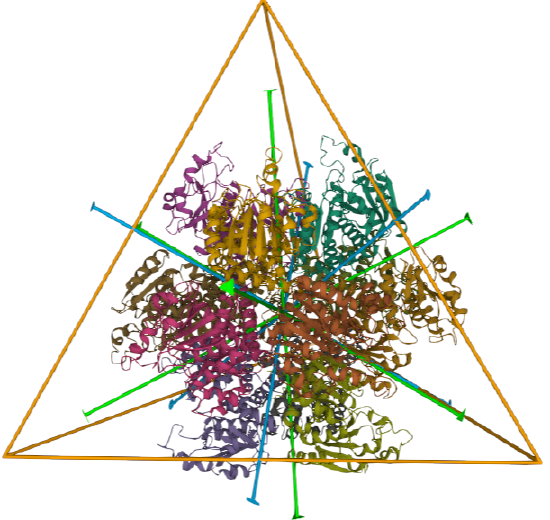 |
Octahedral - 8 sided
C3 axes - line connecting two opposite faces for an octahedron. Since an octahedron can be aligned with a cube, it also has the same symmetry axes. Examples include human ferritin, octahedral, 24 asymmetric subunits. octahedral, homo 24-mer (4V6B) and dihydrolipoyl acyltransferase from Azotobacter vinelandii, octahedral, homo 24-mer (1DPB)
| Protein (pdb) | Symmetry/Homo X-mer (click link) |
Structure - subunits | Symmetry |
| human ferritin (4V6B) | octahedral/homo 24-mer | 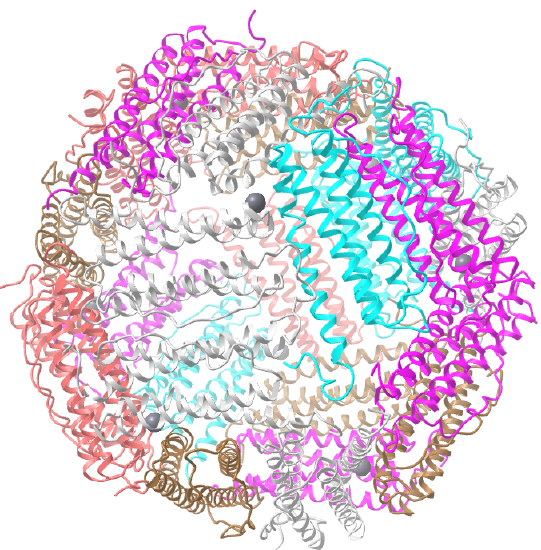 |
 |
| dihydrolipoyl acyltransferase from Azotobacter vinelandii (1DPB) | octahedral/homo 24-mer | 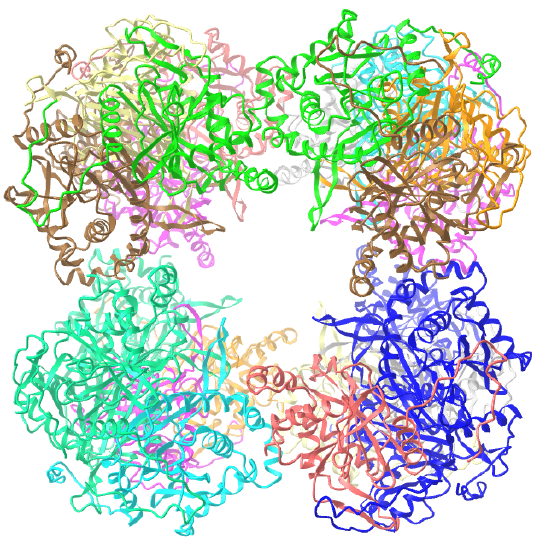 |
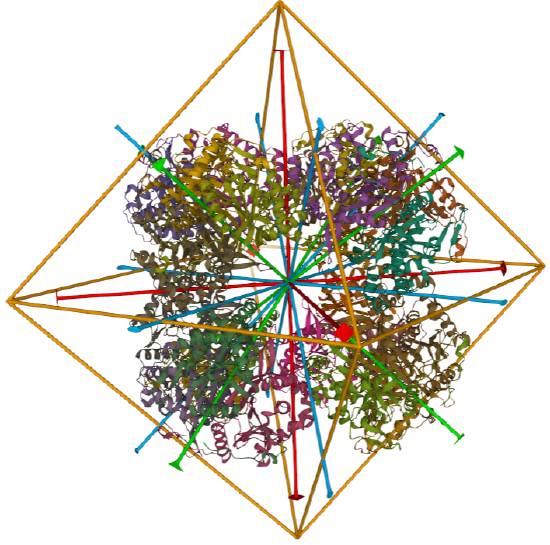 |
Icosohedral - 20 sided, 60 mers
Examples include adenovirus Ad3 virus, Icosahedral , homo 60-mer 4AQQ and dihydrolipoyl transacetylase from Bacillus stearothermophilus, iscosohedral,homo 60-mer (1B5S)
| Protein (pdb) | Symmetry/Homo X-mer (click link) |
Structure - subunits | Symmetry |
| Adenovirus Ad3 virus (4AQQ) | Icosahedral/homo 60-mer |  |
 |
|
dihydrolipoyl transacetylase from |
iscosohedral/homo 60-mer |  |
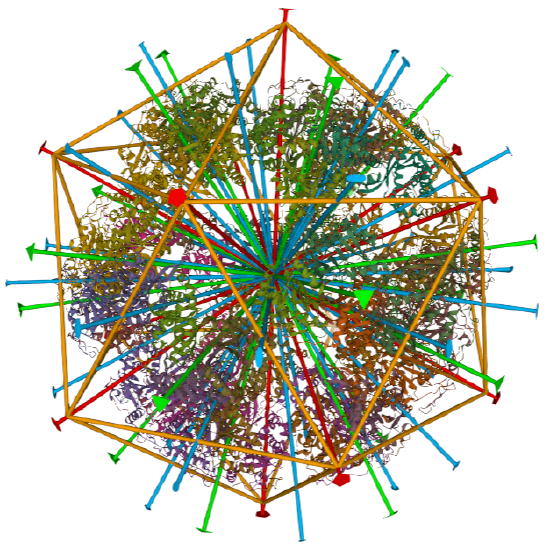 |
In summary, our study of symmetry is not in vain since almost half of all proteins appear to form complexes of identical or similar monomers. This probably stabilizes them and adds functional attributes such as kinetic regulation of their activities. Homo n-mers display symmetry, with Cn and Dn being the most common. The cubic symmetries are far less common. What is interesting about cubic symmetries is that structures displaying cubic symmetries have significant empty interior volumes, or "holes" which can be used to encapsulate chemical species. They include the icosahedral viruses, whose interiors contain proteins and viral genomes, and cellular ferritin, which houses up to 4500 Fe3+ (oxidized) ions in the form of hydroxide and phosphate complexes. Ferritin delivers Fe2+ into cells. Storing iron ions in ferritin prevents its spurious and harmful oxidation and precipitation in nonregulated environments. The encapsulated available volumes have diameters ranging from about 2-4 nm for tetrahedral, 4-8 nm for octahedral and 8-18 nm for icosahedral symmetries.
Filaments
Proteins, especially those involved in cytoskeletal filaments, can form fibers with helical symmetry which differs from those described above since the monomers at the ends of helical fibers, although they have the same tertiary structures as those in the middle of the helical fibers, do not contact the same number of monomers as monomers internal in the oligomer. Hence they have different microenvironments.
Grueninger et al. address the question of whether the process of oligomerization can be programmed into the genome. Can simple amino acid substitutions lead to oligomerization? Oligomerization can be beneficial (formation of cytoskeleton filaments) or detrimental (formation of fibers in sickle cell anemia and prion disease). Oligomers with long half-lives (for example cytoskeletal filaments such as actin and tubulin) and short half-lives (for example proteins that are associated with transient biological activities) are regulated by oligomer formation.
It has long been noted that if a protein chain forms oligomers, then a single amino acid change in the chain would be found n times in an oligomer of n chains. Mutations could either promote chain contact and oligomer formation or dissociation into monomeric or other asymmetric subunit composition if the mutation were in a region involved in subunit association (a contact region). Experimental work in this field of study is hampered by the fact that mutants made by site-specific mutagenesis to prefer the monomeric state often fail to fold (due to hydrophobic exposure and aggregation). Studies have shown that most contact areas between monomers or other asymmetric units are hydrophobic in nature and the contact regions must be complementary in shape. Obviously, mutations that replace hydrophobic side chains involved in subunit contact with polar, polar charged, or bulkier hydrophobic side chains would inhibit oligomer formation.
Grueninger et al were able to successfully engineer dimer formation and oligomer formation as well. First, consider the simplest case of a mutation in a monomer that can produce a dimer with C2 symmetry. This is illustrated below in Figure \(\PageIndex{10}\). The figure illustrates how a mutation that produces a weak interaction in a monomer could also produce a long helical aggregate (which can't be crystallized) without symmetry (as described above). A mutation at 2 could promote either oligomer helix formation or dimerization.
It should be noted that mutation could lead to dimer or oligomer formation by producing a more global conformational change in the monomer (not indicated in the example above) which leads to aggregate formation, as we have seen previously in the formation of dimers and aggregates of proteins associated with neurodegenerative diseases (like mad cow disease).
Grueninger produces mutants of two different proteins that showed dimer formation as analyzed by gel filtration chromatography (but did not crystallize so no 3D structures were determined). In addition, the group modified urocanase, a C2 dimer, at 3 side chains to form a tetramer with D2 symmetry. Also, they modified L-rhamnulose-1-phosphate aldolase, a C4 tetramer, at a single position to form an octamer with D4 symmetry. The latter two were analyzed through x-ray crystallography. Their work suggests ways that complex symmetric protein structures arose in nature from simple mutation and evolutionary selection.
References
OpenStax, Proteins. OpenStax CNX. Sep 30, 2016 http://cnx.org/contents/bf17f4df-605c-4388-88c2-25b0f000b0ed@2.
File:Chirality with hands.jpg. (2017, September 16). Wikimedia Commons, the free media repository. Retrieved 17:34, July 10, 2019 from commons.wikimedia.org/w/index.php?title=File:Chirality_with_hands.jpg&oldid=258750003.
Wikipedia contributors. (2019, July 6). Zwitterion. In Wikipedia, The Free Encyclopedia. Retrieved 21:48, July 10, 2019, from en.Wikipedia.org/w/index.php?title=Zwitterion&oldid=905089721
Wikipedia contributors. (2019, July 8). Absolute configuration. In Wikipedia, The Free Encyclopedia. Retrieved 15:28, July 14, 2019, from en.Wikipedia.org/w/index.php?title=Absolute_configuration&oldid=905412423
Structural Biochemistry/Enzyme/Active Site. (2019, July 1). Wikibooks, The Free Textbook Project. Retrieved 16:55, July 16, 2019 from en.wikibooks.org/w/index.php?title=Structural_Biochemistry/Enzyme/Active_Site&oldid=3555410.
Structural Biochemistry/Proteins. (2019, March 24). Wikibooks, The Free Textbook Project. Retrieved 19:16, July 18, 2019 from en.wikibooks.org/w/index.php?title=Structural_Biochemistry/Proteins&oldid=3529061.
Fujiwara, K., Toda, H., and Ikeguchi, M. (2012) Dependence of a α-helical and β-sheet amino acid propensities on teh overall protein fold type. BMC Structural Biology 12:18. Available at: https://bmcstructbiol.biomedcentral.com/track/pdf/10.1186/1472-6807-12-18
Wikipedia contributors. (2019, July 16). Keratin. In Wikipedia, The Free Encyclopedia. Retrieved 17:50, July 19, 2019, from en.Wikipedia.org/w/index.php?title=Keratin&oldid=906578340
Wikipedia contributors. (2019, July 13). Alpha-keratin. In Wikipedia, The Free Encyclopedia. Retrieved 18:17, July 19, 2019, from en.Wikipedia.org/w/index.php?title=Alpha-keratin&oldid=906117410
Open Learning Initiative. (2019) Integumentary Levels of Organization. Carnegie Mellon University. In Anatomy & Physiology. Available at: https://oli.cmu.edu/jcourse/webui/syllabus/module.do?context=4348901580020ca6010f804da8baf7ba.
Wikipedia contributors. (2019, July 16). Collagen. In Wikipedia, The Free Encyclopedia. Retrieved 03:42, July 20, 2019, from en.Wikipedia.org/w/index.php?title=Collagen&oldid=906509954
Wikipedia contributors. (2019, July 2). Rossmann fold. In Wikipedia, The Free Encyclopedia. Retrieved 16:01, July 20, 2019, from https://en.Wikipedia.org/w/index.php?title=Rossmann_fold&oldid=904468788
Wikipedia contributors. (2019, May 30). TIM barrel. In Wikipedia, The Free Encyclopedia. Retrieved 16:46, July 20, 2019, from en.Wikipedia.org/w/index.php?title=TIM_barrel&oldid=899459569
Wikipedia contributors. (2019, July 16). Protein folding. In Wikipedia, The Free Encyclopedia. Retrieved 18:30, July 20, 2019, from https://en.Wikipedia.org/w/index.php?title=Protein_folding&oldid=906604145
Wikipedia contributors. (2019, June 11). Globular protein. In Wikipedia, The Free Encyclopedia. Retrieved 18:49, July 20, 2019, from en.Wikipedia.org/w/index.php?title=Globular_protein&oldid=901360467
Wikipedia contributors. (2019, July 11). Intrinsically disordered proteins. In Wikipedia, The Free Encyclopedia. Retrieved 19:52, July 20, 2019, from en.Wikipedia.org/w/index.php?title=Intrinsically_disordered_proteins&oldid=905782287