17.4: Maintenance of Mutualisms

Maintenance of mutualism

The stability of mutualisms can be undermined by cheating. Cheating is a behavior whereby organisms receive a benefit at the cost of other organisms. Cheating is common in many mutualistic and altruistic relationships (Ferriere et al. 2002). A cheater is an individual who does not cooperate (or cooperates less than their fair share) but can potentially gain the benefit from others cooperating (West et al. 2006). Cheaters are also those who selfishly use common resources to maximize their individual fitness at the expense of a group (McLean and Gudelj 2006). Simple two-player game theory and the associated evolutionary theory indicate that cheating can be evolutionarily stable, but there are mechanisms to regulate it (Foster and Kokko 2006).

The mutualism between legume plants and rhizobia (nitrogen-fixing soil bacteria) is an example where this regulation occurs. Rhizobia establish symbiotic organs termed root nodules on the roots of their host, and proliferate by extracting nutrients from the host plant. In turn, they supply their host plants with nitrogen resources produced by nitrogen gas fixation. This mutual nutrient exchange should promote the fitness of both organisms and thereby strengthen the symbiotic relationship. This beneficial effect, known as “partner fidelity feedback”, is assumed as a stabilizing factor for the mutualistic relationship (Sachs et al. 2004, Weyl et al. 2010, Friesen and Jones 2012, Friesen 2012).

On the other hand, naturally occurring rhizobium strains vary in their nitrogen fixation activity, and ineffective rhizobia that colonize their host plants without undertaking nitrogen fixation in their root nodules are ubiquitous (Gibson et al. 1975, Bottomly and Jenkins 1983, Moawad 1998, Burdon et al. 1999). Because the nitrogen fixation reaction consumes much energy (or costs), such parasitic cheaters could use surplus energy for their own growth or for synthesizing storage substances. Consequently, they are likely to proliferate more efficiently than nitrogen-fixing cooperators, posing a risk to the symbiotic interaction. Rhizobia are therefore exposed to two opposite effects that simultaneously promote (by providing benefit) and destabilize (by incurring cost) the mutualistic relationship.

Figure \(\PageIndex{1}\): Nitrogen-fixing nodules in legumes.  Photograph by Wikimedia Commons user Terraprima.

Despite the widespread presence of ineffective rhizobia, the legume–rhizobia symbiosis is evolutionarily stable. Host sanctioning is a potential mechanism that stabilizes the symbiotic interaction, where plants punish more parasitic cheaters by reducing nutrient supply based on their symbiotic performance (Friesen and Jones 2012, Friesen 2012, Kiers and Denison 1998).

Another example is found within the yucca-yucca moth mutualisms.  "Cheating" sometimes happens when the yucca moth deposits too many eggs in one plant. In this case, the yucca plant has little to no benefits from this interaction. However, the plant has a unique way of sanctioning this behavior. While the sanctions against cheating often occurs directly to the individual, in this case, the constraint occurs to the individual's offspring. The yucca plant can "abort" the moths by aborting the flowers. Pellmyr and Huth (1994) found that there is selective maturation for flowers that have low egg loads and high number of scars (and therefore a high amount of pollen). In this way, there is selection against the "cheaters" who try to use the yucca plant without providing the benefits of pollination.

 

Figure \(\PageIndex{2}\): Two yucca moth females in a yucca flower. The female on the right is laying an egg and clearly shows the pollen ball on the underside of her head. The female on the left is actively pollinating with her maxillary tentacles. Photograph by Olle Pellmyr.

Exercise \(\PageIndex{1}\): When should you sanction a cheater?

Yucca plants will drop flowers if their obligate pollinators, the yucca moths, lay too many eggs. This reduces fitness for both the plant and the moth that laid the egg, and is a form of sanctioning by the plant. However, devoting resources to growing a fruit with too many yucca moth larvae on it would reduce the plant's fitness even more than aborting the flower does. If the flower is aborted, the cost to fitness for the pollinator is very high, making this an effective sanction against moths that try to "cheat" the plant by laying too many eggs. 

Neither option is great for the plant - but at what point is it worse for the plant's fitness to retain and invest resources in a flower with too many eggs, rather than dropping the flower and sacrificing any possible surviving seeds? It turns out that most yucca fruits that are retained by the plant contain about 130 seeds, but about 20% of those seeds (26 seeds) are eaten by larvae (Alexander et al). Therefore, plants begin to drop flowers when the number of larvae present are likely to consume more than 20% of the seeds! In the graph below, you can see the probability of retaining versus dropping a flower based on the number of larvae present. This graph was simulated from the real values found by Pellmyr and Huth in their groundbreaking 1994 paper, which showed that mutualisms are not always strictly collaborative, but can involve tension between opposing forces (the plant needs pollination, but doesn't 'want' seeds eaten, the moth needs to lay as many eggs as it can) held in check by natural selection. 

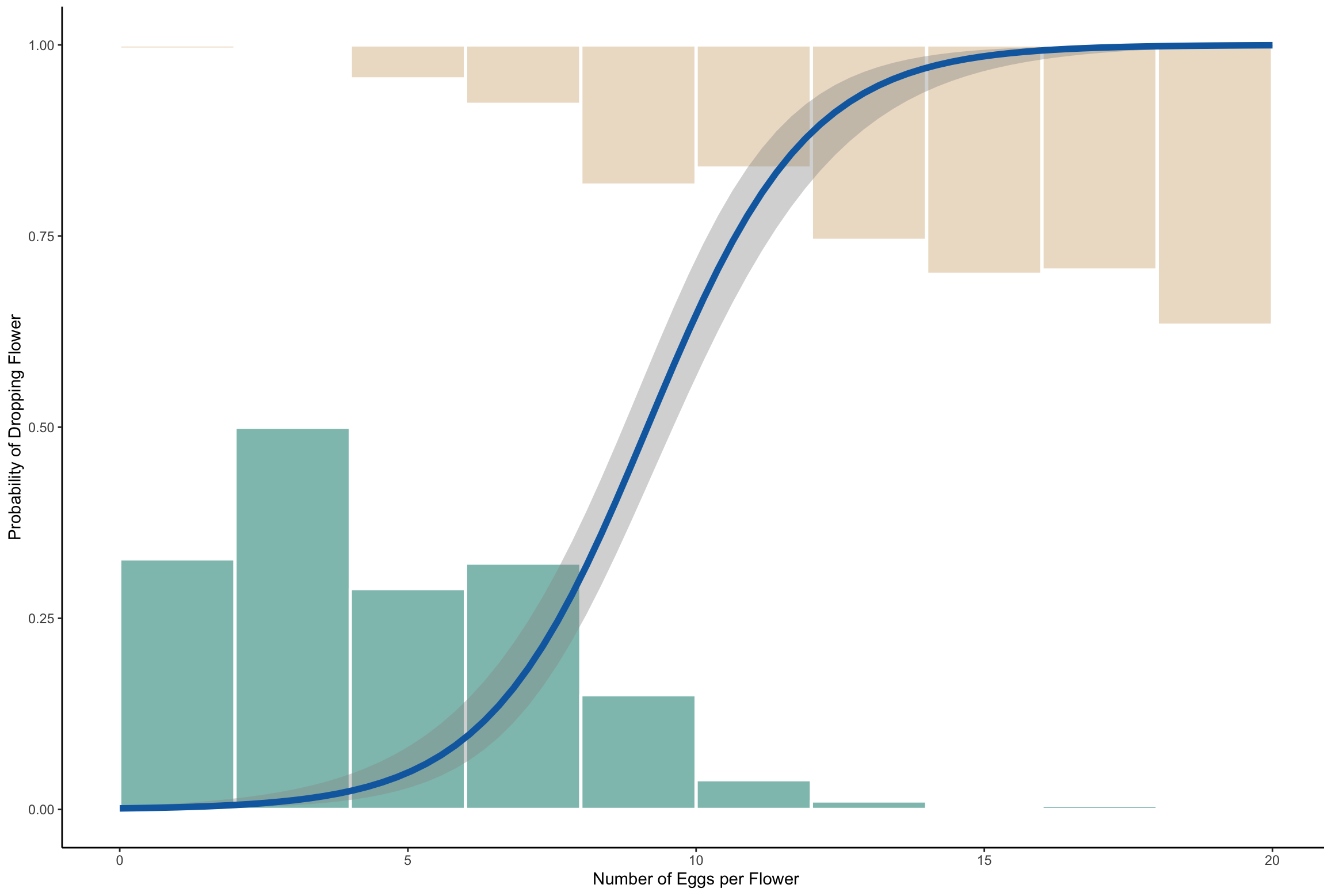
This graph shows the probability of retaining a flower (0) versus aborting a flower (1) based on the number of eggs laid on that flower. As the number of eggs increases, the plant becomes more likely to abort the flower, beginning to switch when there are ~6.5 larvae, meaning that most larvae eat ~4 seeds. However, as you can see from the green (retained) and tan (dropped) histograms, not every plant responds in the same way. Some plants retain flowers even with over 15 eggs laid, while others will drop flowers with only 2 eggs. 

1. How many larvae could a flower tolerate if each flower had 250 seeds, instead of 130? 

2. How many larvae could a flower tolerate if each larva had to eat 10 seeds, instead of 4?

Answer

1. 12.5 larvae

2. 2.6 larvae

 

Attributions

This chapter was written by Aaron Howard with text taken from the following CC-BY resources. Exercise text, data simulation, and code written by Castilleja Olmsted: 

• Cheating (biology) by Wikipedia, the free encyclopedia
• Fujita H, Aoki S, Kawaguchi M (2014) Evolutionary Dynamics of Nitrogen Fixation in the Legume–Rhizobia Symbiosis. PLoS ONE 9(4): e93670. doi:10.1371/journal.pone.0093670

 

References 

Alexander, R. R.; Pond, F. W.; Rodgers, J. E. n.d. Yucca (L.). Forest Service Handbooks. https://www.fs.fed.us/rm/pubs_other/wo_AgricHandbook727/wo_AgricHandbook727_1175_1177.pdf

Ferriere, R.; Bronstein, J.L.; Rinaldi, S.; Law, R.; Gauduchon, M. (2002). "Cheating and the evolutionary stability of mutualisms". Proc. R. Soc. Lond. 269 (1493): 773–780. doi:10.1098/rspb.2001.1900. PMC 1690960. PMID 11958708.

West, S. A.; Griffin, A. S.; Gardner, A.; Diggle, S. P. (2006). "Social evolution theory for microorganisms". Nature Reviews Microbiology. 4 (8): 597–607. doi:10.1038/nrmicro1461. PMID 16845430. S2CID 18451640.

MacLean, R. C.; Gudelj, I. (2006). "Resource competition and social conflict in experimental populations of yeast". Nature. 441 (7092): 498–501. Bibcode:2006Natur.441..498M. doi:10.1038/nature04624. PMID 16724064. S2CID 4419943.

Jump up to:^a b c d Foster, K. R.; Kokko, H. (2006). "Cheating can stabilize cooperation in mutualisms". Proceedings of the Royal Society B: Biological Sciences. 273 (1598): 2233–2239. doi:10.1098/rspb.2006.3571. PMC 1635526. PMID 16901844.

Sachs J, Mueller U, Wilcox T, Bull J (2004) The evolution of cooperation. Quart Rev Biol 79: 135–160.

Weyl EG, Frederickson ME, Yu DW, Pierce NE (2010) Economic contract theory tests models of mutualism. Proc Natl Acad Sci U S A 107: 15712–15716. 

Friesen ML, Jones EI (2012) Modelling the evolution of mutualistic symbioses. Methods Mol Biol 804: 481–499.

Friesen ML (2012) Widespread fitness alignment in the legume-rhizobium symbiosis. New Phytol 194: 1096–1111.

Gibson A, Curnow B, Bergersen F, Brockwell J, Robinson A (1975) Studies of field populations of Rhizobium: Effectiveness of strains of Rhizobium trifolii associated with Trifolium subterraneum L. pastures in South-Eastern Australia. Soil Biol Biochem 7: 95–102.

Bottomley P, Jenkins M (1983) Some characteristic of Rhizobium meliloti isolates from alfalfa fields in Oregon. Soil Sci Soc Am J 47: 1153–1157.

Moawad H, El-Din S, Abdel-Aziz R (1998) Improvement of biological nitrogen fixation in Egyptian winter legumes through better management of Rhizobium. Plant Soil 204: 95–106.

Burdon J, Gibson A, Searle S, Woods M, Brockwell J (1999) Variation in the effectiveness of symbiotic associations between native rhizobia and temperate Australian Acacia: within-species interactions. J Appl Ecol 36: 398–408.

Kiers E, Denison R (2008) Sanctions, Cooperation, and the Stability of PlantRhizosphere Mutualisms. Annu Rev Ecol Evol Syst 39: 215–236

Pellmyr, O.; Huth, C. J. (1994). "Evolutionary stability of mutualism between yuccas and yucca moths". Nature. 372 (6503): 257–260. Bibcode:1994Natur.372..257P. doi:10.1038/372257a0. S2CID 4330563.