1.15: Deviations from Mendelian Genetics- Linkage (Part 2)
- Page ID
- 73680
At the completion of this lesson, you will be able to:
- Make predictions about inheritance using map unit distances and genetic markers.
- Assemble maps from multiple-point linkage data.
- Define the relationship between linkage maps, linkage groups and genome maps.
- Describe how DNA or molecular markers are observed and used in gene mapping.
In this lesson you will learn to make predictions about inheritance using map unit distances and genetic markers, assemble maps from multiple-point linkage data, define the relationship between linkage maps, linkage groups and genome maps, and describe how DNA or molecular markers are observed and used in gene mapping.
Introduction
Why do geneticists map genes? This is a legitimate question after all this discussion. Gene mapping helps geneticists do two things, make better predictions and isolate genes. The following is an example of how gene mapping can help breeders make better selections.
Gene Maps and Selection
This example shows how gene mapping has a practical application. Soybeans have perfect flowers that self-pollinate. Tedious flower manipulation is required to make a hybrid seed. Soybean breeders would like to find ways to make hybrid seeds in commercial quantities. They have discovered a gene that causes a lack of pollen formation and makes plants male-sterile. Therefore, when bees visit these plants, they will make a cross-pollination and produce hybrid seed if they carry pollen from a nearby male-fertile plant. A hybrid seed production field could be set up if they could have all male-sterile plants in one row and male-fertile in the next. The genetic control of this trait is shown below:
Male-fertile plants: MM or Mm
Male-sterile: mm
Can you see the problem one would have in generating seed that is all male-sterile (genotype mm)? These plants will never be true breeding because they cannot self-pollinate (they have working female parts but no pollen). The only plants that can be self-pollinated to produce mm offspring are Mm plants. Progeny from selfed Mm plants will segregate 3 fertile to 1 sterile, making it impossible to obtain a pure collection of mm seeds to plant in a ‘female’ row for hybrid seed production. If the mm genotype could be picked out in seeds prior to planting, this would solve the problem. Unfortunately, the male sterile trait is impossible to select for in the seed but breeders discovered a trick they could use that took advantage of their knowledge of gene maps. A second trait in soybean that is easy to select for in seeds is controlled by a gene that was closely linked to the M,m male sterile gene. This trait is green vs. yellow seed coat. The seed coat trait is controlled as follows:
GG or Gg: green
gg: yellow
The G,g locus and M,m locus have been mapped and are about two map units apart. Therefore, we can take advantage of this linkage to select seeds from a cross that will tend to also be male sterile. This is how the process would work. The following cross is made:
GGMM (green, male-fertile) X ggmm (yellow, male sterile)
The cis dihybrid (GM/gm) will be male-fertile and can be self-pollinated. Because of linkage, the GM and gm parental gametes are made 98% of the time. Therefore, seeds that are gg and yellow are almost always going to be mm and male sterile. If the breeder sorts out the F2 seeds based on color, about one fourth of the seeds will be yellow. Based on 2-map unit distance, about 0.24 would be the expected frequency of ggmm out of all the F2 but 96% of the yellow F2 will be male sterile (0.24 out of 0.25). Therefore 96 out of 100 seeds planted in the ‘female’ row of selected yellow seeds will be male-sterile (mm). Harvesting seeds from these rows will provide a high percentage of hybrid seeds. Thus, the breeder took advantage of linkage to select for a trait that was easy to detect (yellow seeds) and obtain individuals with a trait that was impossible to select (male-sterile). The power of this prediction potential has driven much of the recent efforts in gene mapping in crop plants, livestock, and humans.
0.49 big G, big M
0.01 big G, little m
0.01 little g, big M
0.49 little g, little m
0.49 big G, big M
0.01 big G, little M
0.01 big G, little m
0.01 little g, big M
0.0001
0.0049
0.49 little g, little m
0.0049
0.2401 (selected)
Three Point Test Cross: Multiple Point Gene Mapping
Gene mappers are motivated to map all of the tens of thousands of genes found on the chromosomes of plant or animals. Analyzing data from crosses to determine map distances for two genes at a time makes the process time-consuming and tedious. Therefore, geneticists will often attempt to map as many genes as possible from a single set of progeny. We will go through the simplest multiple point mapping example, a three-point testcross, to demonstrate this process.
We will use our three corn seed trait loci again and use data from one cross to map these three loci. The first step would be to obtain a trihybrid individual that is heterozygous at all three loci and then perform a testcross with this trihybrid.
Parents: CCssWW (CsW/CsW) X ccSSww (cSw/cSw)
Trihybrid: CcSsWs (CsW/cSw) X ccssww (csw/csw)
|
Seed trait |
Gamete from trihybrid
Number
Red, shrunken, normal
CsW
2777
White, plump, waxy
cSw
2708
Red, plump, waxy
CSw
116
White, shrunken, normal
csW
123
Red, shrunken, waxy
Csw
643
White, plump, normal
cSW
626
Red, plump, normal
CSW
4
White, shrunken, waxy
csw
3
Total number of progeny:
7000
We observe eight phenotypes of seeds in the testcross progeny because the trihybrid can make eight kinds of gametes. As we knew, these three genes are linked and so the uneven ratio of phenotypes reflects the combinations of two parental and six recombinant gametes. The parental gametes are still the most frequently produced type, and the six recombinant gametes are made when crossing over occurs between the loci. We can systematically account for these crossovers if we follow the following four steps. First, we will explain the steps and then we will show how to use them to map the three genes.
Step 1: Identify the parental gametes.
These are CsW and cSw, that combination which came from the parent generation and the combination made by the trihybrid at the highest frequency.
Step 2: Classify the recombinants.
If we observe the gene combination in each of the six recombinant gametes, we can ask ourselves if the gamete has a new combination for each pair of genes. For example, CSw has a new combination for the CS and the Cw compared to the parental gametes but the same combination for Sw as the cSw parental gamete. Therefore, these 116 gametes represent crossovers between C,c and S,s as well as C,c and W,s. This information is recorded (see below).
Step 3: Determine recombinant gamete frequency.
Once all six recombinant gametes have been classified, the total number of crossovers between the three loci can be added up and crossover percentage determined between each pair of loci. This number will reflect gene distance but one more step is needed to complete the process.
Step 4: Add in the double crossover gametes.
Two of the six recombinant gametes were made as a result of double crossovers between the two loci that are furthest apart. These crossovers have been added to the map distances between the middle locus and the two outside loci. Now we need to add these double crossovers to the outside loci distance.
Applying these four steps to our three-point test cross data would work as follows:
- CsW and cSw
- C,c to S,s: 116 (CSw) + 123 (csW) + 4(CSW) + 3(csw) = 246
C,c to W,w: 116 (CSw) + 123 (csW) + 643 (Csw) + 626 (cSW) = 1508
S,s to W,w: 643 (Csw) + 626 (cSW) + 4 (CSW) + 3 (csw) = 1276 - 246 / 7000 = 3.5% recombinant gametes C,c to S,s 1508 / 7000 = 21.5% recombinant gametes.
C,c to W,w 1276 / 7000 = 18.2% recombinant gametes S,s to W,w. - From the information in step 3 we can see that the C,c and W,w loci are the farthest apart so the S,s locus must be between them. We can also see that we have underestimated the distance between the outside loci (3.5 C,c to S,s + 18.2 S,s to W,w = 21.7 map units not 21.5). While this difference is small, we can rectify this and double check our work by adding in the double crossovers. The CSW and csw gametes are made very rarely. That is because is takes two crossovers in the trihybrid’s chromosome to make them, not just one.
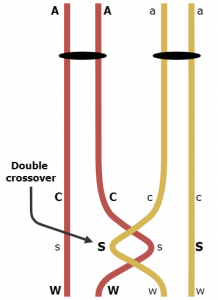
When two crossovers occur between the C,c and W,w loci the parental combinations of CW and cw are restored. Therefore, we did not count the CSW and csw gametes as representing crossovers when they actually represent two crossovers each (Figure 1). Thus, we should add up the double crossovers (3 + 4 = 7), multiply times two and add these 14 crossovers to the C,c to W,w distance (1508 + 14 = 1522 / 7000 = 21.7 map units). Now we have double checked our map distances and have our three-point map complete.
It can be intimidating to see all the data generated from a three-point test cross. This information, however, can be used systematically to save the geneticists time and map three genes in one experiment. The three point data also provides a more accurate measure of map distances compared to two-point data when genes are farther apart on a chromosome. This is because a third gene in between the more distant loci can account for double crossovers that would not be detectable in a two-point analysis. For this reason, map distances tend to be underestimated when genes are further apart as we saw to a modest extent in this example (21.5 two-point vs. 21.7 three-point).

How would a geneticist work with a four-point test cross? There would be sixteen phenotypes in the progeny as a result of the hybrid parent making two parental gametes and fourteen recombinant gametes. These recombinant gametes would be a result of single, double, and even triple crossovers that occurred in prophase I. While the data would be tedious to work with, one data set could be analyzed to reveal the map of four genes. It is not surprising that geneticists now have written computer programs which will perform these types of calculations, save time, and reduce the chance of calculator error. Geneticist’s mapping genes in economically important plants and animals will also generate mapping populations that are a result of crossing parents that have different alleles at hundreds or thousands of loci. Even though the development of computers and programs has become a part of modern gene mapping the process of indirectly measuring crossover frequency by observing the inheritance of trait combinations is the basis of generating these gene maps.
Linkage Maps, Linkage Groups
The organism that gene mapping was first performed in was fruit flies. Working with fruit flies gave the early gene mappers many advantages. First, the fruit fly geneticists observed a great of deal of genetic variation among fruit flies for body part traits (wing size, eye shape and color, leg bristle types etc.) that were easy to see if they had a low powered microscope. The phenotype variants arose naturally or could be induced by chemical or radiation mutagenesis. Additionally, short generation time, large offspring numbers and low rearing costs allowed them to complete informative linkage experiments in a short time. Finally, cytogeneticists knew that fruit flies had four pairs of chromosomes so all the genes would map into four linkage groups. One chromosome was very small, and few genes mapped to this chromosome. The X-chromosome and the largest autosome have many genes and more than 100 map units separate genes on opposite ends of the chromosome.
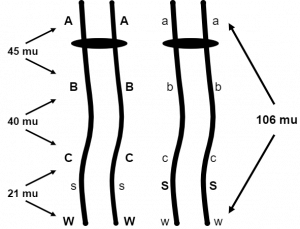
Let’s stop and think about how they determined this large map unit distance. If the A,a and W,w loci are 106 map units apart, how frequently will an AW / aw dihybrid make the gametes Aw and aW? Since these are the recombinant gametes and map distance is the frequency of recombinant gametes, we are tempted to say 106% but that is impossible. The parental gametes for any two loci will never be made less than 50% of the time, the percentage we observe when two loci are independently assorting. In fact, 50% is the correct answer here. Anytime genes that are on the same linkage group are 50 map units or more apart, they will behave as if they are independent of one another. That is because the genes are far enough apart to always allow at least one crossover to occur between them during prophase I. So how can we ever determine that A,a and W,w are 106 map units apart? Simply by determining the distances between these genes and other genes in between them that are less than 50 map units apart (Figure 3). Figure 3 shows that distances can be found between A,a and B,b, B,b and C,c, then C,c and W,w. Each of these distances is added to arrive at the 106 map units between A,a and W,w. Therefore, if the geneticist combines the mapping information from many linkage experiments or performs a multiple point linkage analysis on a progeny group segregating for many linked genes, they can deduce the larger map unit distances.
Limited Traits, Limited Linkage Maps
Many gene mappers do not enjoy the advantages that fruit fly geneticists have in mapping genes. Cattle for example have thirty linkage groups (2n = 60), they often have one offspring per cross, and it is difficult of observe hundreds of phenotype differences controlled by single genes among cattle. Soybean have 20 linkage groups but for many decades, soybean geneticists had compiled about 30 different linkage maps and had no idea as to which maps were really part of the same linkage group. Soybean geneticists needed to discover more genes that had clear phenotype effects and then perform crosses that compared the inheritance of these new genes with the genes that had already been mapped. In the 1970’s and 1980’s, a new type of genetic trait, molecular markers, was discovered that greatly accelerated the gene mapping process in all organisms.


