Genetics
- Page ID
- 23981
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. Description of Genetics.
Information that will guide the development of an organism is contained in that organism’s DNA. Every species has a characteristic number of DNA molecules called chromosomes. An individual receives one complete set of chromosomes from each parent, resulting in two complete sets. This is the diploid condition (2n).
Chromosomes
Chromosomes occur in pairs called homologous chromosomes. One from each parent.
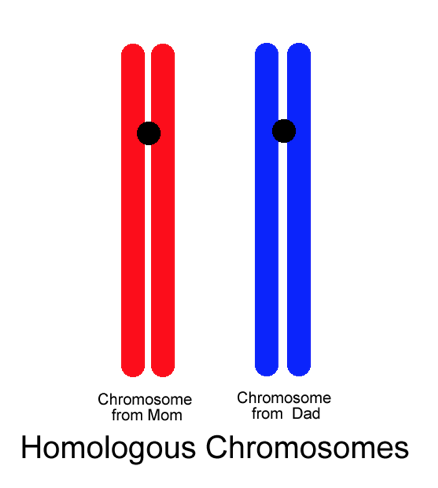
Figure \(\PageIndex{1}\). (CC BY-NC-SA; N. Wheat)
Genes are the functional unit of heredity. Chromosomes are made up of genes that code for traits. A gene is found at a specific location or locus on a chromosome.
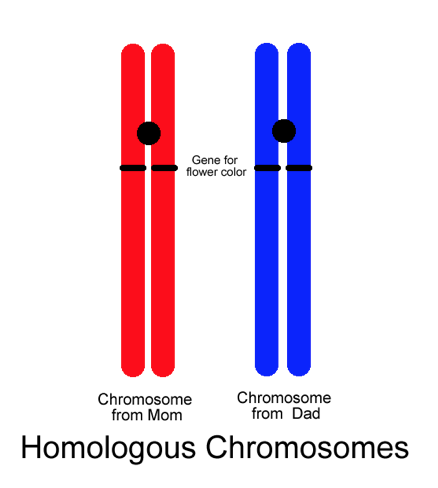
Figure \(\PageIndex{2}\). (CC BY-NC-SA; N. Wheat)
Genes & Alleles
Different versions of genes are called alleles.
- Purple flowers vs. white in pea plants
- Gene= flower color, allele= white or purple
There can be any number of alleles for a given gene, although an individual can have only two alleles(one on each homologous chromosome).
- A, B, O blood type in humans
Some traits are controlled by just one gene, others are influenced by many genes (polygenic).
- Height in humans
Homozygous & Heterozygous
Since an individual has two sets of chromosomes, it will have two copies of each gene (one originally coming from each parent). These two copies may be the same allele, or they may be different.
- Homozygous– both alleles are the same.
- Heterozygous– two different alleles.
Dominant & Recessive
A trait is dominant if it is expressed in an individual with one or two copies of the allele:
- Purple flower color in peas: P= purple p= white. ( The dominant allele is represented by a capitol letter, recessive by the lower case letter.)
- PP – homozygous dominant – two copies of the dominant (purple) allele.
- Pp – heterozygous– one purple allele, one white allele (flowers appear purple).
The trait is said to be recessiveif it is necessary for an individual to have two copies of the allele in order to express the trait.
- pp – two white flower alleles (homozygous).
Genotype
Genotype refers to the alleles that are actually present.
- PP,Pp,ppin our flower color example.
- The purple phenotype may have PP or Ppgenotype.
Phenotype
Phenotype refers to the visible or expressed characteristics of the trait.
- What does it look like?
- Purple or white for our flower color example.
Heredity – Passing on Traits
An individual can pass on genetic information to its offspring. In order to avoid doubling the number of chromosomes in each generation, cells must be created that carry only one set of chromosomes (haploid or 1n).
An individual can pass along either of the two alleles it carries for a trait, but not both.
A Pp individual can pass on either P or p.
These haploid cells (eggs or sperm) are formed during meiosis.
Meiosis
Meiosis is a type of cell division that occurs in two parts.
Before division starts, each chromosome makes a copy of itself. These identical copies (called sister chromatids) remain connected at the centromere.
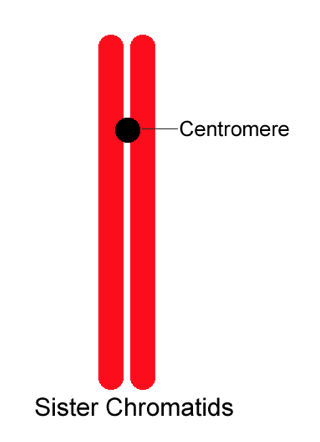
Figure \(\PageIndex{3}\). (CC BY-NC-SA; N. Wheat)
In the first part of meiosis, homologous chromosomes are separated.
- The cells are now haploid.
During the second part of meiosis, the sister chromatids are pulled apart.
- This part is like regular cell division (mitosis).
The division of one diploid cell will result in 4 haploid cells.
- Each cell is different.
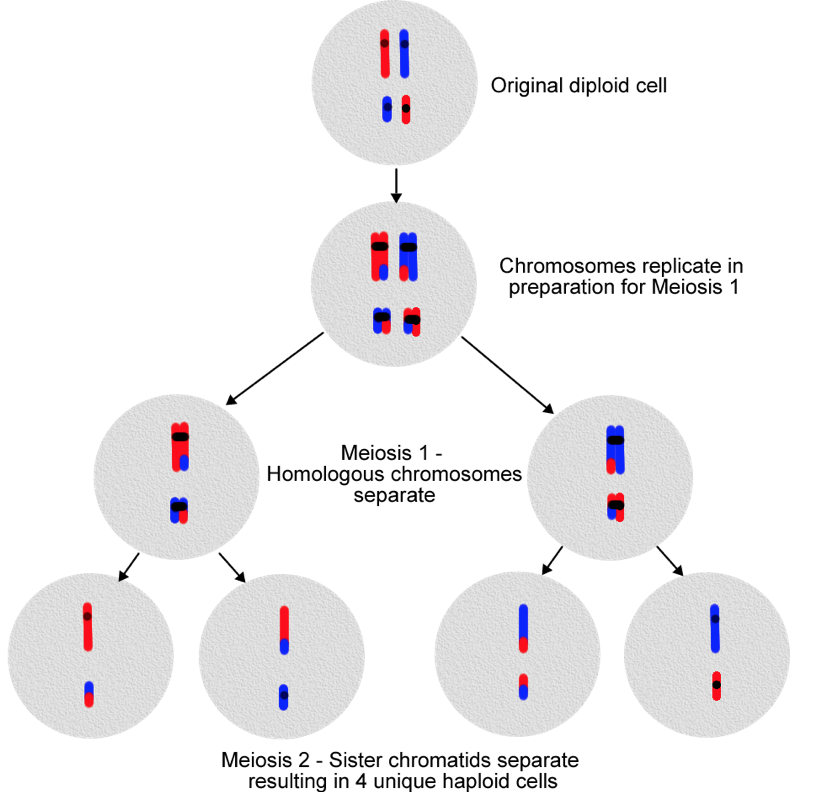
Figure \(\PageIndex{4}\). (CC BY-NC-SA; N. Wheat)
We can look at how traits are passed from one generation to another individually or two at a time using a Punnett square.
For our example, we will use the ball python. There are many mutations that breeders want to incorporate into their animals.
- Albino – a simple recessive trait
- Pinstripe – a dominant pattern mutation
Punnett Square – 1 Trait
First let’s focus on the albino trait. It is recessive so:
- AA & Aa individuals will have normal coloration.
- aa individuals will be albino.

Figure \(\PageIndex{6}\). (CC BY-NC-SA; N. Wheat)
In a monohybrid cross we will cross two animals that are heterozygous for albino.
- Aa x Aa
- We want to know, statistically, what kind of offspring to expect.
- Each parent can donate only one allele for the albino gene.
- A heterozygote (Aa) can donate either an A or an a– not both.
- An albino must receive an a from both parents.
Place the alleles that may be donated by each parent across the top and along the sides.
Fill in the boxes:
- 1AA - normal
- 2Aa – normal, heterozygous for albino
- 1aa - albino
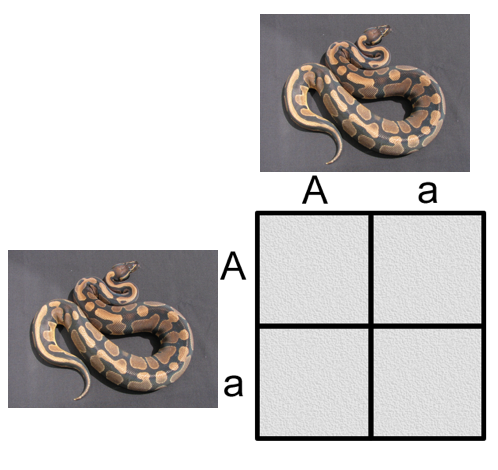
Figure \(\PageIndex{7}\). (CC BY-NC-SA; N. Wheat)
Punnett Square – 2 Traits
We can also use the Punnett square to track two traits at once. Remember each gamete (egg or sperm) will contain one allele for each trait. So, the possible combinations of alleles that we will place on our Punnett squares will always have one letter for each trait.
Again, we want to know, statistically, what kind of offspring to expect.
Each parent (AaPp) will donate either an A or an a allele for the albino gene and either a P or a p allele for the pinstripe gene. So every gamete will always contain ONE A (or a) andone P (or p).
We can use the FOIL method from math to be sure that we have all of the possible combinations of alleles.
- First, Outer, Inner, Last
Next, we fill in each square. By convention, we put the alleles for one gene together followed by the second:
- Aapp not Apap
Also, any dominant alleles are placed before recessives.
- AaPp not aApP
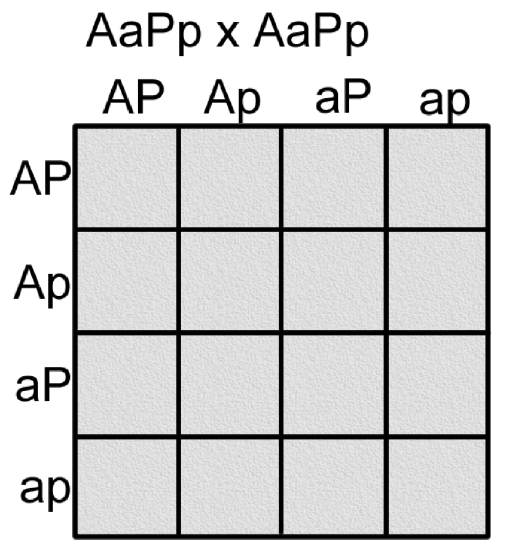
Figure \(\PageIndex{8}\). (CC BY-NC-SA; N. Wheat)
Genotypes from DihybridCross
The Punnett square gives us the genotypes that result from the cross.
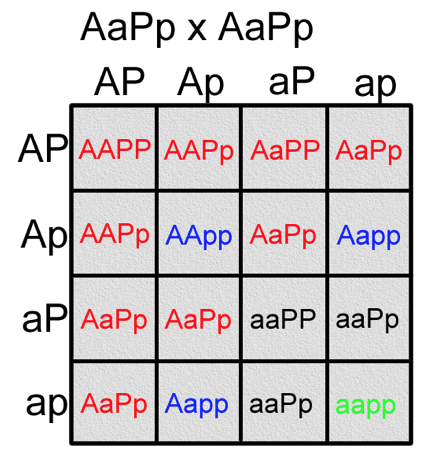
Figure \(\PageIndex{9}\). (CC BY-NC-SA; N. Wheat)
The phenotypes would be:
- 9 Pinstripe (A_P_)
- 3 Normal (A_pp)
- 3 Albino pinstripe (aaP_)
- 1 Albino (aapp)
Albino is a recessive trait, while pinstripe is a dominant trait. The 9:3:3:1 phenotypic ratio is characteristic of a dihybrid cross.
The Product Rule
Punnett squares are very useful for tracking one or two traits, but they can become unwieldy when looking at more than two traits. The product rule is a simple way to determine the likelihood of getting a particular result from any cross, regardless of the number of traits involved.
To use the product rule, we determine the likelihood of getting each trait individually, then multiply those probabilities together. We’ll use our dihybrid cross example to start with.
- AaPp x AaPp
We need to look at the traits separately:
- Aa x Aa. There would be a 1 in 4 chance of hatching an albino from this cross.
- Pp x Pp. Pinstripe is dominant so ¾ of the offspring will be pinstripes.
What is the chance of getting an albino pinstripe from this cross?
¼ x ¾ = 3/16
This is the same result that we got using the Punnett square.
We can look at as many traits as we want using the product rule. Say we are interested in combining these 4 traits:
- Pinstripe (dominant) – (PP, Pp, pp)
- Albino (recessive) – (AA, Aa, aa)
- Piebald (recessive) – (BB, Bb, bb)
- Hypo (recessive) – (HH, Hh, hh)
The parents have the following genotypes: AaPpBbhhx aappBbHh
Calculate probability of getting individual traits:
- Albino – Aa x aa = ½
- Pinstripe – Pp x pp = ½
- Piebald – Bb x Bb = ¼
- Hypo – hhx Hh= ½
½ x ½ x ¼ x ½ = 1/32 = chance of getting an animal that shows all 4 traits from this pairing.
This tutorial was funded by the Title V-STEM Grant #P031S090007.


