1.2: Metrics and Measurements

Last updated
Save as PDF

Page ID: 36744

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Goals:

Review the metric system.
Learn to convert between metric units.
Use various instruments found in the biotechnology lab.
Measure mass and volume with precision and accuracy.
Pipet with precision and accuracy.
Learn how to use a micropipette to measure very small volumes.

Student Learning Outcomes:

Upon completion of this lab, students will be able to:

Convert between metric units for mass, volume and size.
Use a gram balance to obtain the mass of an object.
Make accurate and precise measurements with a graduated cylinder and serological pipette.
Calculate percent error for a given measurement.
Read, set, and operate a micropipette.
Determine which pipette should be used to measure a specific volume.
Determine how accurately you can measure with each micropipette.

Part 1: Metrics

Introduction to Metrics

Working in a biotechnology lab requires knowledge of the metric system. The metric system uses standardized units of measurement for length, mass, and volume, ensuring measurements are reproducible and easily made. Appropriate instruments are used to make these measurements. For example, balances measure mass in grams and graduated cylinders measure volume in milliliters.

The metric system has base measurements. The meter is used to measure distances; the liter measures volume; and the gram measures mass. A measurement must always consist of a number and a unit, for example, 2 m, conveys the length is twice that of the base unit of length, the meter. The abbreviations are permitted when expressing measurements. The metric system allows for easy conversion between units as everything is base 10. This means you will either multiply or divide by ten as you convert from one unit to another. For example, one decameter is 10 times larger than a meter. Therefore, you need 10 meters to equal a decameter. A kilometer is 1000 times larger than a meter. Therefore, you need 1000 m to equal one kilometer.

Base Units of Measure

Length: meter (m)
Mass: gram (g)
Volume: liter (L)
Time: seconds (s)
Temperature: Celsius (C)

Metric Prefixes
Prefix	Unit	Multiplier	Scientific Notation
Kilo-	k	1,000	$10^3$
Hecto-	h	100	$10^2$
Deca-	da	10	$10^1$
One	base (m, L, g)	1	10
Deci-	d	0.1 = $1/10$	$10^{-1}$
Centi-	c	0.01 = $1/100$	$10^{-2}$
Milli-	m	0.001 = $1/1,000$	$10^{-3}$
Micro-	µ	0.000001 = $1/1,000,000$	$10^{-6}$

Converting Metric Units

Memorize the table above and know how to use metric prefixes. You can use the helpful mnemonic below.

Mnemonic for remembering metric conversions
Mnemonic	King	Henry	Does	Usually	Drink	Chocolate	Milk
Prefix	Kilo-	Hecto-	Deca-	Base units	Deci-	Centi-	Milli-	Micro
unit	k	h	da	m, L, g	d	c	m	µ

When you are converting a smaller unit to a larger unit, you move the decimal point to the left the appropriate number of steps. Keep in mind each time you move the decimal point you are dividing by 10.

When you are converting from a larger unit to a smaller, you will move the decimal point to the right. This means each time you move the decimal point you are multiplying by 10.

Steps for Converting Metric Units

Write down the number you are converting for example (100 cm). Then right in the decimal point. It is always right after the ones place to the right of the number.
100 = 100
If you want to convert 100 cm to meters (m) you would now look at your chart and determine how many “steps” you have to move the decimal to the right or left. From centimeter to meter you have to take 2 steps to the left. That means you must move your decimal 2 places to the left.
100. cm = 1.00 meters

Metric Conversion Practice

Using the steps above, complete the following problems in your lab notebook.

50 mm = X cm
50 cm = X km
700 mL = X L
30 m = X µm
3 dm = X m
15 kg = X cg
55 L = X mL
52 mg = X µg

Part 2: Measuring Using the Metric System

A. Taking Linear Measurements with a Ruler

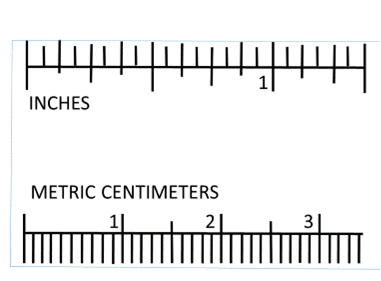
Linear measurements in science are in metric units. The basic unit is the meter (m). The rulers you will be using today are centimeter (cm) rulers. There are 100 cm in a meter. If you look at the ruler, you will see 10 hatch marks between each centimeter marking. Each hatch mark represents a millimeter (mm). There are 10 millimeters in a centimeter.

ruler showing inches and centimeter scale — Figure 1. Ruler: centimeter scale bottom. Inch scale top.

Figure 2. diameter of washer, measured in a straight line across the center of the washer from outer edge to outer edge.

Materials

5-6 washers of various sizes
Centimeter ruler

Procedure

Obtain 5 washers from your instructor.
Order the washers on a piece of paper from the smallest diameter to the largest, labeling them #1-5.
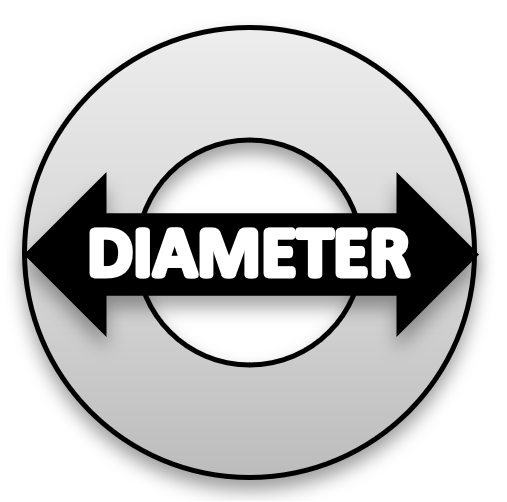
Using a centimeter ruler, record the diameter of each washer in centimeters. See Figure 2 for and image on how to measure the diameter.
Record your results in Table 1.
Convert all your washer diameter measurements to millimeters and meters. Record in Table 1.
Keep your washers in order as you will be using them later.

Results

Draw the following table in your lab notebook including the title of the table.

Table 1. Diameter Measurements of Washers with Unit Conversions
Washer #	Diameter of Washer (cm)	Diameter of Washer (m)	Diameter of Washer (mm)
1
2
3
4
5

B. Taking Mass Measurements with an Electronic Balance

Weight measurements in science are also in metric units. The basic unit is the gram (g). The electronic balances you will be using today are gram balances. The model you will be using will accurately measure to 0.01 gram. There are 1000 grams in a kilogram. One of the most common units used is the milligram (mg). There are 1000 milligrams in a gram. If you need a very small amount of something, you measure it in micrograms (µg). There are $10^6$ µg in a gram. Some conversions are indicated below:

1000 g = 1 kg
1 g = 1000 mg
1 g = 1,000,000 µg (106 µg)
1 mg= 1000 µg

Materials

5 washers of various sizes that were previously measured.
Gram balance

Procedure

Press the on button and wait for the balance to display zeros on screen.
If the screen doesn’t display zeros, press the “zero” or “tare” button.
Once the machine displays zeros (0.00 g), place your washer on the center of the platform.
Wait for the scale to achieve a stable reading (numbers are not fluctuating).
Record your mass in grams in Table 2 for each washer starting from smallest to largest.

Results

Draw the following table in your lab manual including the title.
Record your results in grams (g) and then convert those masses to kg and mgs.

Table 2. Weight Measurements of Washers with Unit Conversions
Washer #	Diameter of Washer (cm)	Diameter of Washer (m)	Diameter of Washer (mm)
1
2
3
4
5

C. Volumetric Measurements

The metric unit for volume is the LITER (L). There are 1000 milliliters (mL) in one liter. Another common unit in volume is the microliter (µL). There are 106 µL in one liter and 1000 µL in one milliliter. Some common conversions are shown below:

1 L = 1000 mL
1 L = 1,000,000 µL (106 µL)
1 ml= 1000 µL

You will need to become familiar with the different types of instrumentation and glassware that you will be using throughout this semester. Today, we will focus on glassware and devices that measure larger volumes of liquid. You will also determine when a particular device is appropriate to use based on the volume that you are dispensing. The types of measuring devices are very different if you want to measure and dispense a liter vs. a milliliter!

Graduated Cylinder

You will use this to dispense large volumes that are more than 10 mL. You will be using various size graduated cylinders, ranging from 20mL – 2000 mL (2L), in this class.

Serological Pipet

These pipettes accurately dispense volumes of 1mL to 10mL and can be used for volumes up to 50 mL. You will be using mostly 5mL and 10mL serological pipettes in this class.

several sizes of graduated cylinders — Figure 3. Graduated Cylinders

various sizes of serological pipettes. — Figure 4. Serological Pipettes

various sizes of beakers. — Figure 5. Beakers

Materials

1 - 50 ml beaker
Squirt bottle with diH20
1 - 50 ml graduated cylinder
1 - gram scale
1 - 5 ml serological pipette
1 pipette pump or electronic pipet aide

Procedure

Graduated Cylinder Measurements

Draw a table 3 in your lab manual as shown on the following page.
Obtain a 50 mL beaker. Weigh and record the weight in grams on Table 3 under “Weight of container”. This is the container you will use to weigh your water. It is not what you will use to measure in this experiment.
The target amount of water you will be measuring using a graduated cylinder is 42 mL. This has been recorded in Table 3.
Using a squirt bottle, squirt 42 mL of water into a graduated cylinder. Be sure to read from the bottom of the meniscus.
Pour the 42 mL from the graduated cylinder into the weighed beaker.
Weigh the beaker with the water and record on Table 3 under “weight of container and water.”
Determine the weight of the water and record as “weight of water only”.
Convert this weight to mL. Water has a density of 1g/mL. Because water has a density of 1g/mL, then the number g=mLs (50ml=50g) Record this number as “actual volume dispensed”.
Determine the % error for each of your measurements as follows:
$∖ [" id="MathJax-Element-5-Frame" role="presentation" style="position:relative;" tabindex="0"> ∖ [$

Serological Pipet

Dry the 50 ml beaker you used previously. You already weighed this container in the previous exercise. Write the weight of the container you previously attained.
Obtain a 5 mL serological pipet and a pipet pump. Put on the pipet pump. Do not shove the pipet way up into the pump. Use the dial to draw 3.7 mL of deionized water into the pipet from a 50 mL graduated cylinder.
Dispense the water into the weighed beaker dialing in the opposite direction. To get the last bit out of the pipet, quickly dial one way then the other.
Dispense the 3.6 mL into the weighed beaker and determine its mass (g). Record this value in your table as “weight of container and water.”
Determine the weight of the water and record. If you accurately dispensed 3.6 mL, the weight difference should be very close to 3.6 g.
Convert the weight to mL and record.
Determine the % error as described in the previous section and record on Table 3.
If you are not with in an error range of +/- 5% then try again

Results

Table 3. Determining the Accuracy of Measurements of Water Volumes
Device used	Attempt	Target volume dispensed (mL)
50 mL graduated cylinder	trial #1	42
50 mL graduated cylinder	trial #2 (if needed)	42
5 mL serological pipet	trial #1	3.6
5 mL serological pipet	trial #2 (if needed)	3.6

D. Accuracy and Precision

When making measurements, both precision and accuracy are extremely important. Precision of a measurement refers to the closeness of repeated measurements or the reproducibility of the measurement (how small the range is), while accuracy describes how close the measurement is to the true value or expected value.

Precision can be affected by the measuring instrument. If a student uses a thermometer calibrated to the nearest degree to measure the temperature of a beaker of water and a second student uses a thermometer that is calibrated to the nearest ten degrees for the same exercise, the reproducibility or precision of measurements will be greater for the student using the thermometer calibrated to the nearest degree. The thermometer with the greatest number of calibrations (smallest increments) is the most precise, and thus the reproducibility is greater.

Accuracy, however, is dependent upon both the precision of the measuring instrument and the technical skills of the individual taking the measurement. You will perform an experiment to determine which instrument is most accurate and precise for measuring 10ml of liquid. Once you have obtained your group data, we will use Google Docs to create a spreadsheet with the class data. You will use the class data set to determine which instrument was most accurate and most precise.

To calculate the “mean” or “average”, you will add all the measurements and then divide by the number of measurements. For example, if three groups weighed a washer and the measurements for weight were 9 grams, 11 grams, and 10 grams, to calculate the mean you would add 9+10+11 and then divide by 3 (because there were 3 measurements) and you would get a mean of 10 grams. To calculate the range, you would take the smallest measurement and subtract that from the largest measurement. In the last example, the range would be 11-9, which would give you a range of 2. As a class we will fill in the following tables and you will include them in your lab notebook (making sure to give EACH table a title!!).

Materials

1 - 50 ml beaker
Squirt bottle with diH20
1 - 25 ml graduated cylinder
1 - gram scale
1 - 10 ml serological pipette
1 pipette pump or electronic pipet aide

Procedure

Obtain a 50 mL beaker. Place the beaker on the scale and hit “tare.” This will cancel out the weight of the beaker.
Obtain a second 50 mL beaker and use it to measure 10 mL of deionized water. Pour the measured 10 mL of water into the 50 mL beaker on the scale. Record the weight in grams under the number “1” in table 1-5 (which means that this is your first attempt to measure 10 mL with the beaker), which is equivalent to the mL of water (because remember that water has a density of 1 g/mL).
Dispose of the water in the beaker that is on the scale. Dry the beaker between measurements. Repeat steps 1-3 for a total of 4 trials using a beaker to measure 10 mL water.
Obtain a 25 mL graduated cylinder and measure 10 mL of deionized water. Pour the measured 10 mL of water into the 50 mL beaker on the scale. Record the weight in grams under the number “1” (which means that this is your first attempt to measure 10 mL with the graduated cylinder), which is equivalent to the mL of water (because remember that water has a density of 1 g/mL).
Dispose of the water in the beaker that is on the scale. Repeat steps 4-5 for a total of 4 trials using a graduated cylinder to measure 10 mL water.
Obtain a 10 mL serological pipet and measure 10 mL of deionized water. Pour the measured 10 mL of water into the 50 mL beaker on the scale. Record the weight in grams under the number “1” (which means that this is your first attempt to measure 10 mL with the serological pipet), which is equivalent to the mL of water (because remember that water has a density of 1 g/mL).
Dispose of the water in the beaker that is on the scale. Repeat steps 6-7 for a total of 4 trials using a serological pipet to measure 10 mL water.
When finished, dump out all the water and place your used glassware on the cart in the front of the room.
Determine the average and the range for your data for each measuring device and record in table 4-6.
Record your averages for each measuring device in Table 2.1-2.6 for the class data.
Record your ranges for each measuring device in Table 2.1-2.7 for the class data.

Results

Table 4. Actual Volume Dispense for 4 trials (mL)
Measuring Device to Measure 10 mL	1	2	3	4	Average	Range
beaker
Graduated cylinder
Serological pipet

Table 5. Class Average Actual Volume Dispensed for 4 Trials
Measuring Device to Measure 10 mL	1	2	3	4	Class Average
Beaker
Graduated cylinder
Serological pipet

Table 6. Class Range of Actual Volume Dispensed for 4 trials (mL)
Measuring Device to Measure 10 mL	1	2	3	4	Class Range
Beaker
Graduated cylinder
Serological pipet

Conclusion

Use your data and the questions below to write your conclusion in your lab notebook

For the volume measurements, which glassware used to measure 10 mL was the most precise?
Which measuring device was the least precise? Explain in detail why you think that particular device is the most precise.
For the glassware used to measure 10 mL, which instrument was the most accurate?
Was the instrument that was most precise the same one that is the most accurate?
Why or why not (in your answer be sure to include which measuring device was the most precise and which one was the most accurate)?
What can contribute to a larger % error when making a measurement? If you had to repeat a measurement in Table 3, be sure to indicate why you think your % error was outside of the acceptable range.

Study Questions

Convert the following:
1. 345 mL = X µl
2. 0.34 dag = X kg
3. 5.2 km = X mm
Which equipment would you use to measure 10 mL, 5 mL, 1 mL?
Be able to calculate your percent error.

Search

Text Color

Text Size

Margin Size

Font Type

Learning Objectives

Steps for Converting Metric Units

Metric Conversion Practice

Materials

Procedure

Results

Materials

Procedure

Results

Graduated Cylinder

Serological Pipet

Materials

Procedure

Graduated Cylinder Measurements

Serological Pipet

Results

D. Accuracy and Precision

Materials

Procedure

Results

Conclusion

Study Questions

Prefix	Unit	Multiplier	Scientific Notation
Kilo-	k	1,000	\(10^3\)
Hecto-	h	100	\(10^2\)
Deca-	da	10	\(10^1\)
One	base (m, L, g)	1	10
Deci-	d	0.1 = \(1/10\)	\(10^{-1}\)
Centi-	c	0.01 = \(1/100\)	\(10^{-2}\)
Milli-	m	0.001 = \(1/1,000\)	\(10^{-3}\)
Micro-	µ	0.000001 = \(1/1,000,000\)	\(10^{-6}\)