6.3: Ligand binding
- Page ID
- 18156
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Molecular recognition is a key aspect of virtually all biochemistry, and involves:
- DNA replication
- Gene regulation
- Transcription of DNA into mRNA
- Translation of mRNA into proteins
- Enzyme function
- Molecular assembly
- Signal transduction
- Cell-cell communication
- Immunology
Intermolecular interactions, in the simplest example, involves two molecules recognizing and binding to each other:
- The ligand
- The receptor
These are broad terms, but the general properties of receptor and ligand are as follows:
- The ligand is typically, a small molecule, and it diffuses throughout the environment until it binds to a specific receptor
- The receptor is typically a large, relatively stationary molecule that contains a specific binding site for the ligand. Upon binding ligand, the structural and/or chemical properties of the receptor are typically altered
The interactions between receptor and ligand are typically non-covalent
- There is a general molecular complementarity between the receptor and ligand
- Often, but not always, there is an entropic cost associated with binding of the ligand to receptor, but this is more than offset by a favorable enthalpy (i.e. the molecular complimentarity)
- The binding energy is typically utilized to cause a structural change associated with a molecular communication event
There are two general methods to study receptor/ligand interactions:
-
- Equilibrium thermodynamics, and
- Association and dissociation kinetics
Equilibrium ligand/receptor binding analysis
The two possible states of a ligand/receptor interaction, and the rate constants associated with their formation, are given as:
The equilibrium association (formation) constant, Kf, is given as:
- [RL] is the concentration of the complex, [R] is the concentration of free R at equilibrium, and [L] is the concentration of free Lat equilibrium
- Kf has units of M-1
- A large value for Kf means that the equilibrium favors the complex - there is a high affinity of the receptor for the ligand
- A small value for Kf means that the equilibrium favors the separation of the receptor and ligand, and the receptor has a low affinity for the ligand
Just to make life difficult, the typical frame of reference when describing receptor affinity for ligand is to reference the dissociation constant, Kd:
- Kd has units of M
- A small value for Kd means that the equilibrium favors the complex - there is a high affinity of the receptor for the ligand
- A large value for Kd means that the equilibrium favors the separation of the receptor and ligand, and the receptor has a low affinity for the ligand
At equilibrium, the rate of formation of the RL complex is equal to the rate of dissociation:
The left-hand expression is the definition of the dissociation constant, Kd, therefore:
The free energy expression and Kf and Kd
From the original expression of the complex formation:
The standard state free energy change, ΔG0, for the process (i.e. starting with 1M everything) would be given as:
Since Kd is the inverse of Kf:
In this case, a negative value for DG0 (indicating spontaneity) will occur when Kd < 1.0. This will happen when there is high affinity and the equilibrium favors the complex formation.
Practical relationships between [R], [L], Kd and [RL]
For the same concentration of added ligand and receptor, more complex formation will occur with a smaller value of Kd
Example 6.3.1
Receptor and ligand are added to a total concentration of 1.0 x 10-4M. The Kd for the RL complex is 1.0 x 10-4M. What is the concentration of [R], [L] and [RL] at equilibrium?
.png?revision=1&size=bestfit&width=328&height=93)
The added ligand, L, will be partitioned between free and bound forms:
Ltotal = L + RL = 1.0 x 10-4M
L = 1.0 x 10-4M - RL
Similarly, the added receptor, R, will be partitioned between free and bound forms:
Rtotal = R + RL = 1.0 x 10-4M
R = 1.0 x 10-4M - RL
Substituting these values of L and R into the expression for Kd yields:
.png?revision=1&size=bestfit&width=355&height=180)
This is a quadratic with values a = 1, b = -3.0 x 10-4 and c = 1.0 x 10-8. This yields two possible values for RL:
RL = 2.62 X 10-4M or
RL = 3.82 X 10-5
Since the maximum possible value for [RL] is 1.0 x 10-4 (i.e. given the starting concentrations of R and L, this is the most amount of RL that can be formed), the first result is not possible and [RL] = 3.82 X 10-5M
Thus, 38.2% of the added receptor is in the complex formation (i.e. 3.82 X 10-5M/1.0 x 10-4)x100%
Example 6.3.2
Same amount of added R and L, but this time the Kd for the RL complex is 1.0 x 10-6M. What is the concentration of [R], [L] and [RL] at equilibrium?
.png?revision=1&size=bestfit&width=412&height=205)
his is a quadratic with values a = 1, b = -2.01 x 10-4 and c = 1.0 x 10-8. This yields two possible values for RL:
RL = 1.11 X 10-4M or
RL = 9.05 X 10-5
Since the maximum possible value for [RL] is 1.0 x 10-4 (i.e. given the starting concentrations of R and L, this is the most amount of RL that can be formed), the first result is not possible and [RL] = 9.05 X 10-5M
Thus, 90.5% of the added receptor is in the complex formation (i.e. 9.05 X 10-5M/1.0 x 10-4)x100%
For the same concentration of added ligand and receptor, more complex formation will occur with a smaller value of Kd
Determination of dissociation (Kd) or binding (Kf) constants
The relationship between Kd, [R], [L] and [RL] is given by:
- This is an equation with four variables, if you know three of them, you can solve for the fourth
- In principle, you can solve for Kd if you know the concentration of free receptor [R], free ligand [L] and receptor/ligand complex [RL] at equilibrium
To be able to solve for Kd, you need an assay that will provide the molar concentrations for each component. However, this is typically difficult to achieve. It is much more common to have an assay that will provide you with information regarding the fraction of added receptor (or ligand) that is present in the free or complex form.
- If [Rt] is the total concentration of receptor in the sample, we know that it will be divided into two populations - bound and free:
- The fraction of bound receptor sites is given by the ratio:
- The fraction of bound receptors is known by the variable a, and a has a value between 0 and 1
- Substituting the value for [Rt] in terms of [R] and [RL] given above yields:
- The relationship between [RL] and Kd is given by the expression for Kd:
- This expression for [RL] can be substituted into the expression for a to yield:
- Simplify by first dividing through by [R]:
- Then multiply by Kd:
This equation has three variables:
- The concentration of free ligand at equilibrium [L]
- The dissociation constant, Kd, for the RL complex
- The fraction of receptor that is in the bound form at equilibrium, a
If you know two of these variables, you can solve for the third (i.e. if the experimental assay quantifies [L] and a, you can solve for Kd)
The above equation can be manipulated further by substitution of the value of a in terms of [RL] and [Rt]:
This equation has four variables:
- The concentration of free ligand at equilibrium [L]
- The dissociation constant, Kd, for the RL complex
- The concentration of receptor that is in the bound form at eqilibrium [RL]
- The total concentration of receptor in the sample
Usually, the ligand-binding experiment is setup so that [Rt] is held constant and [RL] is monitored as a function of [L]
This equation looks a lot like the Michaelis-Menten equation:
Plotting V versus [S] in the M-M equation yields a rectangular hyperbola. Thus, plotting [RL] versus [L] will likewise yield a rectangular hyperbola
- The asymptote of the curve will yield the value of [Rt]
- The free ligand concentration [L] that results in one-half the maximum value of [RL] is equal to the Kd value
Yet another modification is to realize that if a equals the fraction of receptor bound in a complex (with a value 0 ≤ α ≤ 1.0), then (1 - α) is the fraction of free receptor (i.e. fraction of unbound receptor)
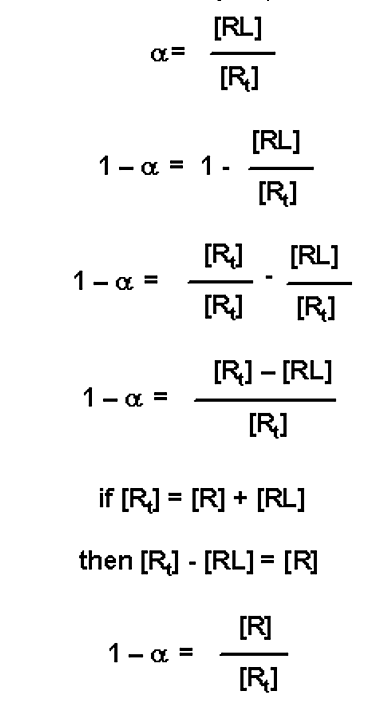.png?revision=1&size=bestfit&width=225&height=426)
This value can be substituted into the three variable expressions above:
.png?revision=1&size=bestfit&width=327&height=452)
This equation has four variables:
- The concentration of free ligand at equilibrium [L]
- The dissociation constant, Kd, for the RL complex
- The concentration of receptor that is in the free form at eqilibrium [R]
- The total concentration of receptor in the sample [Rt]
Usually, the ligand-binding experiment is setup so that [Rt] is held constant and [R] is monitored as a function of [L]
(Note:Although this looks like a M-M equation, Kd is a constant. )
The above derivations are called "binding isotherms" in reference to their ability to solve for Kd under equilibrium conditions (and the original equilibrium thermodynamic equation utilized constant temperature)
.png?revision=1&size=bestfit&width=572&height=227)
Plotting data for various values of [L], [Rt], and either [RL] or [R], and fitting to the appropriate function above, allows a more accurate determination of Kd (although a single experiment will provide an answer).
Due to the similarity of the [RL] versus [L] plot with the M-M plot, it is often the more desirable experimental setup. In particular, a double-reciprocal plot can be used (much like the double-reciprocal M-M plot) to more accurately determine Kd
.png?revision=1&size=bestfit&width=331&height=333)
- If you plot 1/[RL] versus 1/[L] you will get a straight line whose slop is equal to Kd/[Rt]
- Y intercept will be equal to 1/[Rt]. Since this value is fixed and is known, the value of the y intercept can serve as a check to make sure the experiment fits the model
An equilibrium dialysis experiment
A semi-permeable membrane can be used in a dialysis-based equilibrium experiment to determined Kd for a ligand-receptor pair.
- The membrane should be freely permeable as far as the ligand is concerned (usually it is a small molecule), but present a barrier to the receptor
- The experiment is established with a known concentration of receptor on one side, and a known concentration of ligand on the other
- The system is allowed to come to equilibrium
- The experiment requires an assay for the ligand
.png?revision=1&size=bestfit&width=401&height=385)
Figure 6.3.1: Semipermeable barrier
After equilibrium is reached the ligand concentration on both sides of the semi-permeable membrane is assayed:
.png?revision=1&size=bestfit&width=467&height=404)
Figure 6.3.2: Equilibrium concentration
- Since the ligand is unaffected by the membrane te ligand concentration on the side with no receptor is equal to the free ligand concentration [L] everywhere in the sample (i.e. on both sides of the membrane)
- The ligand concentration will be equal to the free ligand concentration [L] plus the ligand present in the receptor complex [RL] (in other words, there should be a higher concentration of ligand on the side with the receptor if the receptor has affinity for the ligand)
- The concentration of the receptor/ligand complex [RL] can be determined from the difference between these two values
- The total receptor concentration is a known value (experimenter determined at the start of the experiment, and does not change)
- Either binding isotherm can be used to solve for Kd (since [R] can also be determined)


