14.2: Basic Principles of Metabolic Control Analysis (MCA)
- Page ID
- 15012
Introduction to Metabolic Control Analysis
Enzyme kinetics may seem difficult given the complicated mathematical derivations, the number of chemical species involved (an enzyme and all its substrates and products), the number of steps in the mechanism, and a large number of rate, kinetic, and dissociation constants. An example of such a “complicated” reaction explored earlier is shown in Figure \(\PageIndex{1}\).

\begin{equation}
v=\frac{\frac{k_2 k_3}{k_2+k_3}\left(E_0\right)(S)}{\left[\frac{k_3}{k_2+k_3}\right] K_S+S}=\frac{k_{c a t}\left(E_0\right)(S)}{K_M+S}
\end{equation}
But single enzymes rarely act in isolation. They are components of complex pathways which have a multitude of steps, many of which are regulated. To fully understand a reaction, it is important to study the concentrations of all species in the entire pathway as a function of time. Imagine deriving the equations and determining all the relevant concentrations and constants of a pathway such as glycolysis!
To study enzyme kinetics in the lab, you have to spend much time developing assays to measure how the concentration of species changes as a function of time to be able to measure the initial velocities of an enzyme-catalyzed reaction. However, in networks of connected metabolic reactions, the concentration of some species in the system may not change. How can this happen? Two simple examples might help explain how.
Example 1: There is no change in input or output from a given reaction. This would occur in a closed system for a reversible reaction at equilibrium.
For a reversible reaction of reactant R going to product P (R ↔ P) with forward and reverse first-order rate constants, the following equation can be written at equilibrium:
\begin{equation}
\begin{gathered}
v_f=k_1 R=k_2 P \\
K_{e q}=\frac{P_{e q}}{R_{e q}}=\frac{k_1}{k_2}
\end{gathered}
\end{equation}
At equilibrium, \(R\) and \(P\) don’t change.
Example 2: Consider the reaction as part of a pathway of reactions (like an open system). Now imagine a nonzero input to form reactant R and a nonzero output that consumes product P as shown in Figure \(\PageIndex{2}\).

If the input and output rates are the same, the concentrations of R and P would not change with time. That is the rate of formation of a reactant R for a given reaction is equal to the rate at which the product P of the given reaction is used. This would lead to a steady state but not equilibrium concentrations of the species.
The Steady State - A Threshold Biochemistry Concept
Students have a difficult time understanding the steady state and recognizing when it may prevail under a set of conditions.
Cornish-Bowden in his book Fundamentals of Enzyme Kinetics talks about key differences between the enzyme kinetics we do in test tubes (in vitro) and what happens in cells (in vivo). We've discussed this previously but it is important to reconsider it now. The conditions under which the enzymes are studied (in vitro) and operate (in vivo) are very different.
- In vitro (in the lab), the enzyme is held at a constant concentration while the substrate is varied (i.e the substrate concentration is the independent variable). The velocity is determined by the substrate concentration. When inhibition is studied, the substrate is varied while the inhibitor is held constant at several different fixed concentrations.
- In vivo (in the cell), the velocity might be held at a relatively fixed level in a pathway with the substrate determined by the velocity. To avoid a bottleneck in flux, substrate can't build up at the enzyme, so the enzyme processes it in a steady-state fashion to produce the product as determined by the Michael-Menten equation
These differences are vastly underappreciated and not understood by students and instructors alike.
Additionally, we confound our efforts in helping students understand the steady state when almost all of our efforts are focused on presenting initial rate v0 vs [S] curves when the substrate concentration is changed. Then instructors expect students to magically understand the steady state when substrate levels in pathways don’t change. It’s a big leap out of this box. We can help students better understand the steady state by shifting to progress curves (concentrations vs time), which are easily constructed by using programs such as VCell and Copasi.
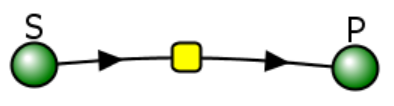
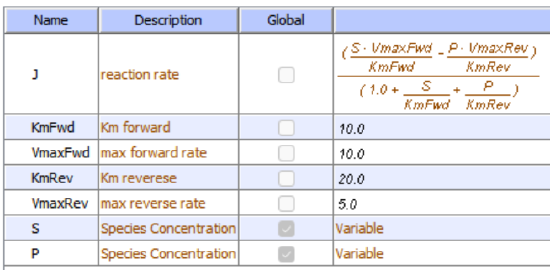
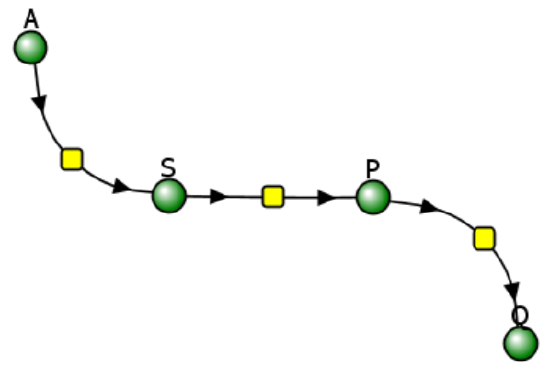
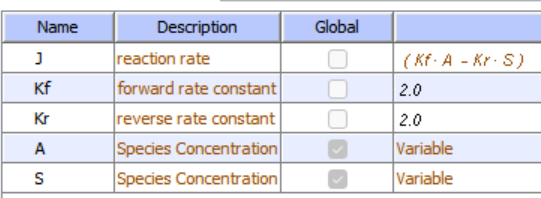
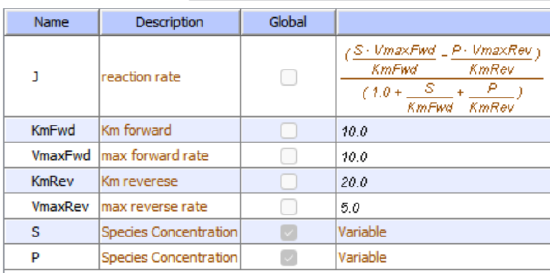
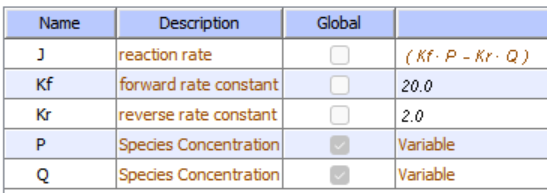
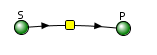
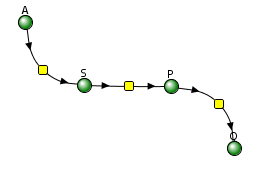
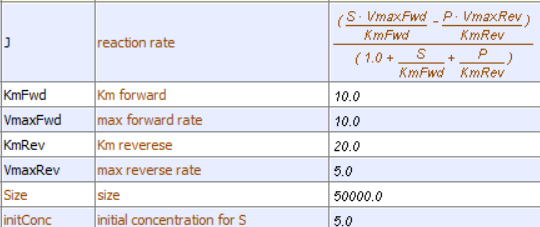
Let's use Vcell to analyze a very simple reversible enzyme in isolation, S ↔ P. Then we will place that same enzyme into a "mini" pathway, A ↔ S ↔ P ↔ Q in which there is one preceding reactant A and one following product Q that help control S and P levels. We have to start the simulation at some specified concentration so the default for the simulations is set such that [S] and [A] at time t = 0, S0 and A0, are 5, and the rest are set at 0. Hence as the simulation starts, there will be a readjustment of concentration until equilibrium or steady state concentration is reached. The reaction diagrams and their parameters are shown in Figure \(\PageIndex{3}\).
| A reversible enzyme in isolation, S ↔ P | A reversible enzyme for S ↔ P in a mini-pathway A ↔ S ↔ P ↔ Q |
 |
 |
 |
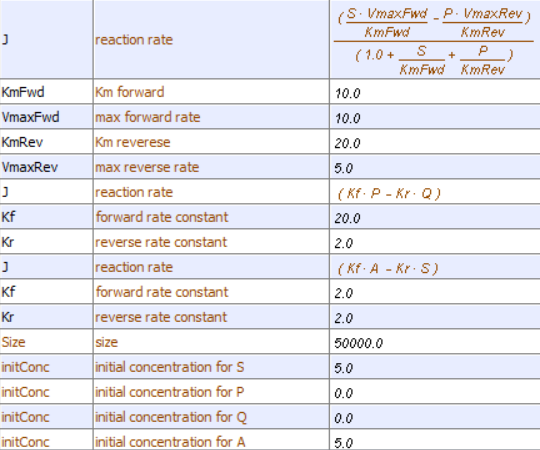 |
Figure \(\PageIndex{3}\): Reactions schemes and parameters for simple enzyme-catalyzed reversible reaction and the same reaction embedded in a "mini" pathway.
Vcell simulation for the isolated enzyme
Remember that an enzyme does not change the thermodynamics of a given reaction and hence doesn't alter Keq. It just speeds up both the forward and the reverse reactions. Hence you can calculate the Keq for the reaction condition from the Vcell model time course graph:
\begin{equation}
\mathrm{K}_{\mathrm{eq}}=\frac{[\mathrm{P}]_{\mathrm{eq}}}{[\mathrm{S}]_{\mathrm{eq}}}=\frac{4}{1}=1
\end{equation}
Now you observe that in this reaction, S does change from its initial value, S0 = 5 (since P0 = 0). Soon, however, the reaction comes to a real dynamic equilibrium in that both S and P don't change with time.
You could choose a different initial concentration of S and P, rerun the simulation and calculate KEQ for the new conditions using the csv-downloaded spreadsheet data fro each run you make. They should be the same.
Vcell simulation for the the enzyme in a "mini-pathway"
Now compare this same reaction but in which S and P are part of the "mini-pathway" A ↔ S ↔ P ↔ Q, as shown in the Vcell model below. The enzyme kinetic parameters for S ↔ P (KM forward, VM forward, KM reverse, VM reverse) in the A ↔ S ↔ P ↔ O pathway were made the same as for the simple S ↔ P reaction since its the same enzyme. How do the A ↔ S and P ↔ Q reactions affect the apparent KEQ? Run the Vcell model with the defaults automatically set to the values in the table above!
As in the first simulation, constant values for S and P are soon reached. Both are significantly lower than in the simple reaction of S ↔ P since P is being pulled toward Q faster than Q is converted back to S. Note also that Q reaches a higher concentration than either A or S but remember that the sum of the initial values of A and S is 10.
Run the simulation again only this time set kr=2000 for the P ↔ Q reaction.
Now calculate the "KEQ apparent" for the different kf values of the conversion of P → Q from this equation. Again use the csv-downloaded spreadsheet data for each run you make.
\begin{equation}
K_{\text {eq apparent }}=\frac{[\mathrm{P}]_{\text {steady state }}}{[\mathrm{S}]_{\text {steady state }}}
\end{equation}
Do they equal 4 as in case 1? No, they do not. You should see that the "KEQ apparent" value deviates most from 4 (lower number) when the rate constant for removal of P is highest (kf=2000).
Animations
Now let's look at some animation for these reactions as an additional way to understand the dynamics of the reactions. Click the image in Figure \(\PageIndex{4}\) to view (in a new window) the animation of the chemical species and an inserted graph showing concentration vs time for the reversible enzyme-Catalyzed Reaction S ↔ P

Pay attention to the disappearance of S (red) and the appearance of P (blue) species after interacting with the enzyme (green).
Now here are two animations for the S ↔ P reaction when its embedded in the "minipathway" A ↔ S ↔ P ↔ Q when kf for the reaction P ↔ Q is 20 (left) and 200 (right). Click the images in Figure \(\PageIndex{5}\) to view (in a new window) an animation of the chemical species and inserted graphs showing concentrations vs time.
| "mini-pathway" A ↔ S ↔ P ↔ Q, kf for the reaction P ↔ Q = 20 | "mini-pathway" A ↔ S ↔ P ↔ Q, kf for the reaction P ↔ Q = 200 |
 |
 |
Figure \(\PageIndex{5}\): Animation of the reversible enzyme-Catalyzed Reaction embedded in a "minipathway" A ↔ S ↔ P ↔ Q when kf for the reaction P ↔ Q is 200.
These animations should reinforce your understanding of the differences between equilibrium and steady-state conditions, although you can calculate the actual KEQ apparent from the insert graphs without numerical data.
Understanding a pure enzyme in vitro and in vivo requires different approaches. Biochemists like to isolate and purify to homogeneity an enzyme found in some tissue and study its mechanism of action. In doing thermodynamic measurements to measure equilibrium constants (Keq) or dissociation constants (KD), from which ΔG0 can be calculated, a protein concentration is usually held constant as the binding ligand concentration is varied (independent variable). A dependent variable signal (often spectroscopic) is measured. Measurements are made when equilibrium is reached.
For enzyme kinetic measurements in vitro, the enzyme concentration is usually held constant while substrate and modifiers are varied (independent variables) to determine how velocity (dependent variable) changes. The velocity is determined by the substrate concentration. When inhibition is studied, the substrate is varied while the inhibitor is held constant at several different fixed concentrations.
In vivo, the substrate concentration and even the enzyme concentration are determined by the velocity. Again compare this to in vitro kinetics when concentrations determine the velocity. For sets of reactions in pathways, it is better to use the term flux, J. In the steady state, the in and out fluxes for a given reaction are identical. Flux J is used to describe the rate of the system whereas rate or velocity v is used to describe the rate of an individual enzyme in a system.
Computer programs can find steady-state concentrations by finding the roots of the ordinary differential equations (ODE) when set to zero (vf = vr). To model a process at very low concentrations, programs can also use probabilistic or stochastic simulations to model probability distributions for species and their change with time for a finite number of particles. In such simulations, concentrations (mM) are placed with the number of particles. ODEs don’t work well to describe these conditions since changes in concentrations are not continuous.
Now back to our earlier rhetorical question of deriving the equations and determining all the relevant concentrations and constants of a pathway such as glycolysis! It has been done by Teusink et al for glycolysis in yeast. Many such complicated metabolic and signal transduction pathways have been mathematically modeled in the hopes of better understanding cellular and organismal responses. Quantitatively modeling and predicting input, outputs, and concentrations of all species in complex pathways is the basis of systems biology.
Basic Principles of Metabolic Control Analysis - Glycolysis
Let's use a more complex example, glycolysis, to illustrate the powers of computational modeling of entire pathways. The reference for this model is shown below.
Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry, Bas Teusink, Jutta Passarge, Corinne A. Reijenga, Eugenia Esgalhado, Coen C. van der Weijden, Mike Schepper, Michael C. Walsh, Barbara M. Bakker, Karel van Dam, Hans V. Westerhoff, and Jacky L. Snoep, 2000, European Journal of Biochemistry, 267, 5313-5329. PubMed ID: 10951190.
Databases containing curated models with all the above information have been developed for many pathways. The yeast glycolysis model described in the reference above and the material below is found in the Biomodels Database. The model, BIOMD0000000064, can be downloaded as a systems biology markup language (SBML) file and imported into any of the programs described above.
A variety of inputs are required for such computational analyses:
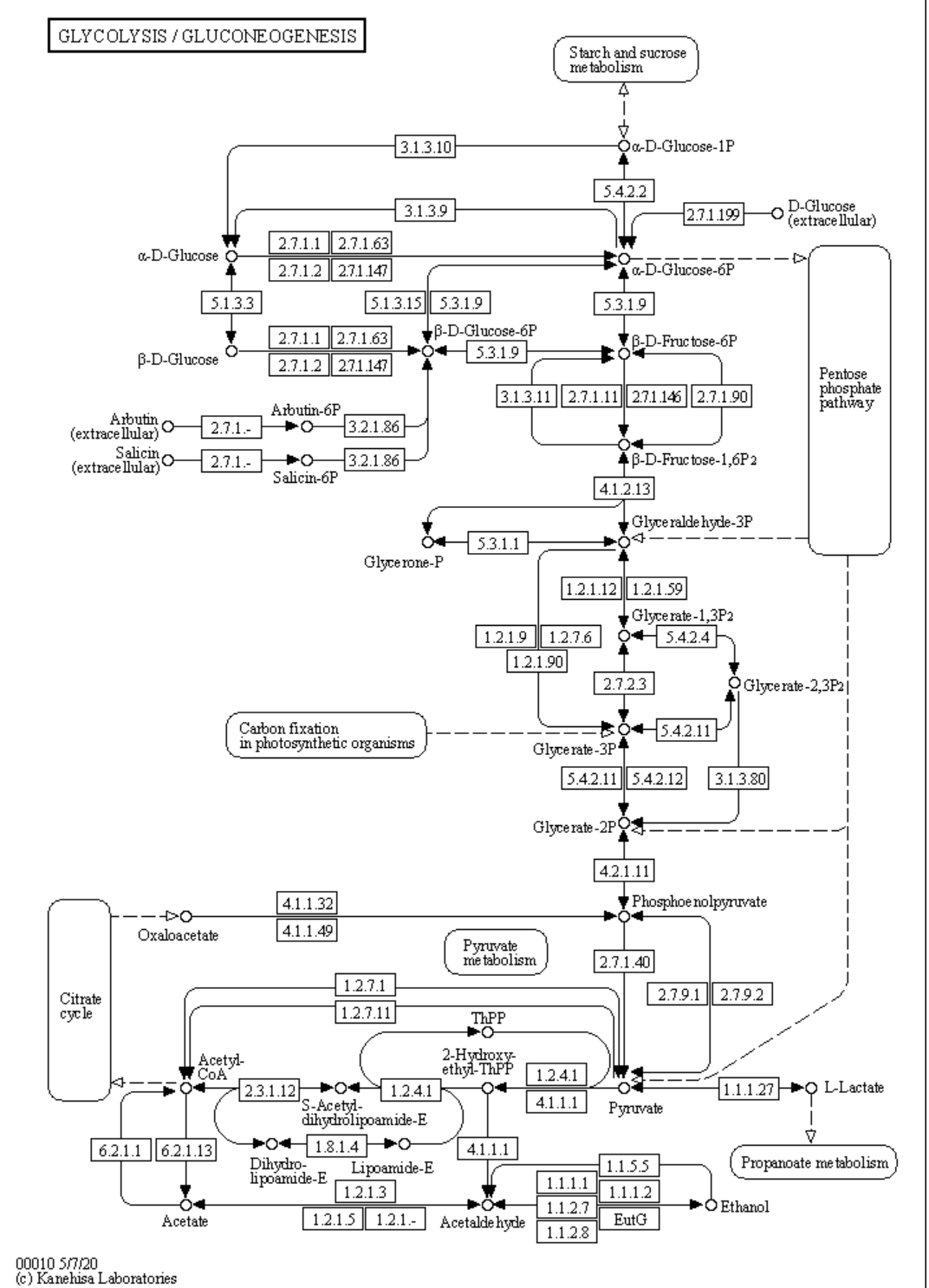
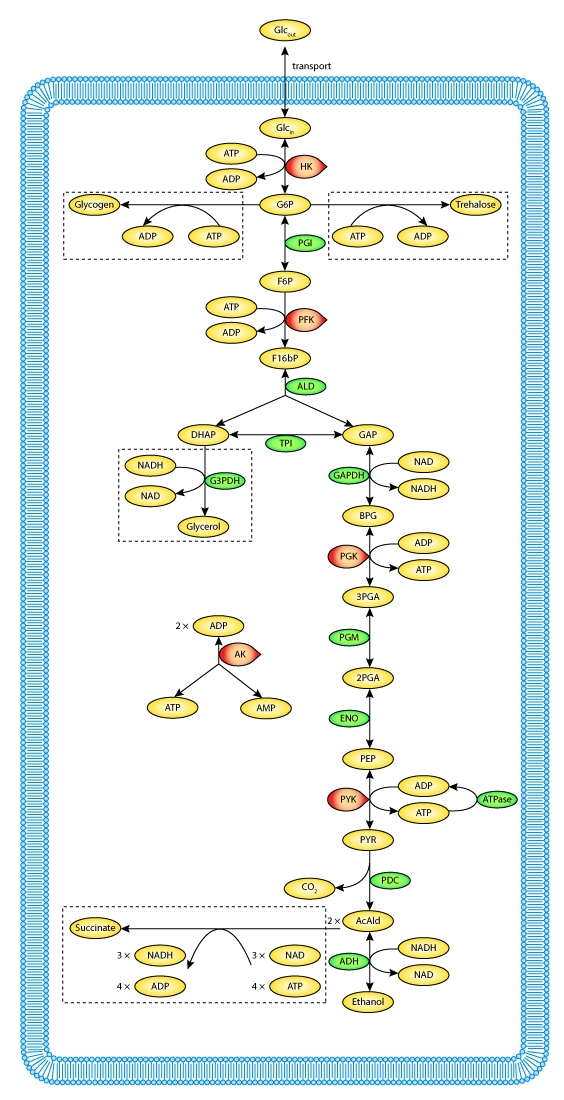
a. Defined pathways. These are available in many databases. An example from the KEGG pathways for yeast glycolysis is shown in the left panel of Figure \(\PageIndex{6}\) below. The right panel shows a more familiar representation, with glucose on the outside of the cell (Glco) entering the cell.
  |
 |
b. A computational modeling program to input all parameters, equations, and models and calculate concentrations for all species as a function of time. We have been using Vcell throughout this book. A reaction diagram is constructed that connects all of the species. Two are shown in Figure \(\PageIndex{7}\) below.
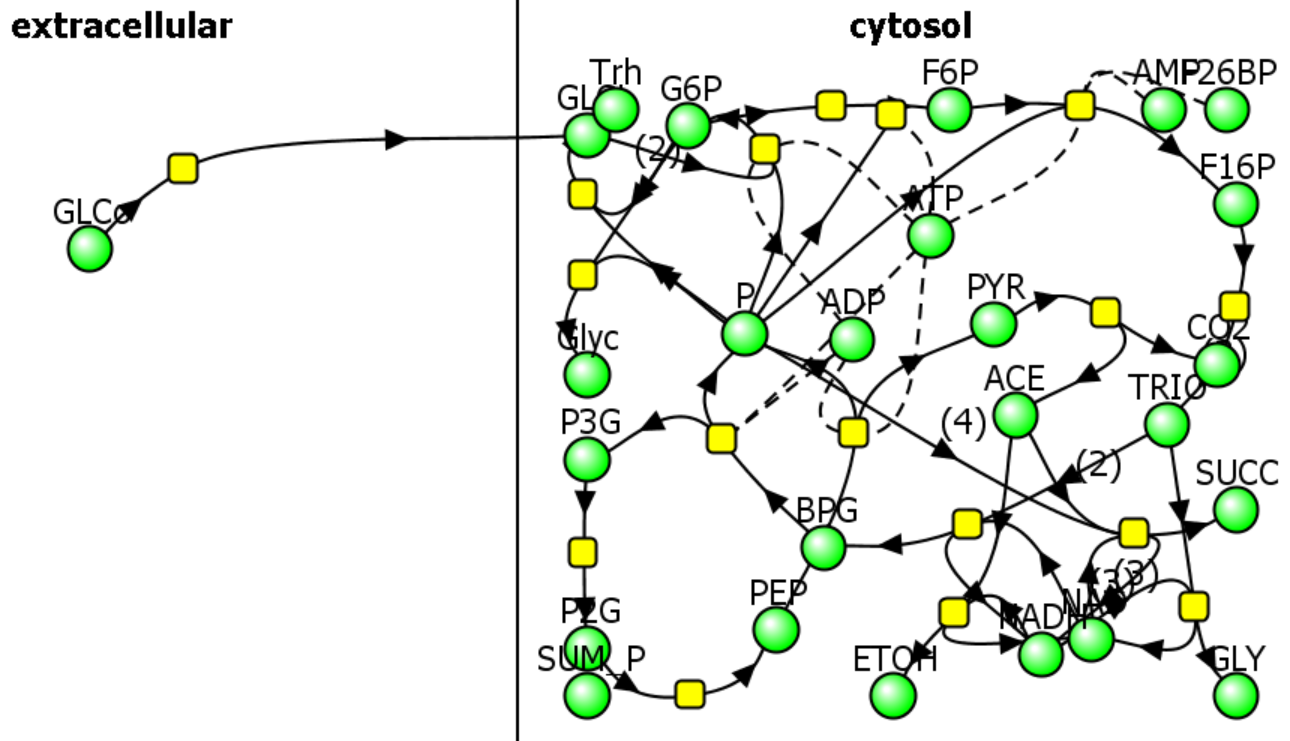 |
The computational results from the analyzes for yeast glycolysis were able to fit experimental data only if corrected by the addition of several branching reactions (shown in the figures above and Figure \(\PageIndex{8}\)) and in the dotted boxes in Figure 6 (Right)
Trehalose is the non-reducing disaccharide Glc-(α 1,1)-Glc. It is a reserve carbohydrate that also protects yeast against the effects of stress (desiccation, dehydration, temperature extremes) as well as lethal levels of ethanol. These effects arise from its effects on protein stability which likely arise by its preferential exclusion from the hydration sphere of protein. A similar mechanism accounts for the stabilizing effect of glycerol on protein stability, as described in Chapter 4.9.
c. A list of all reactions as shown in Figure \(\PageIndex{10}\) for glycolysis and branching reactions (taken from COPASI).
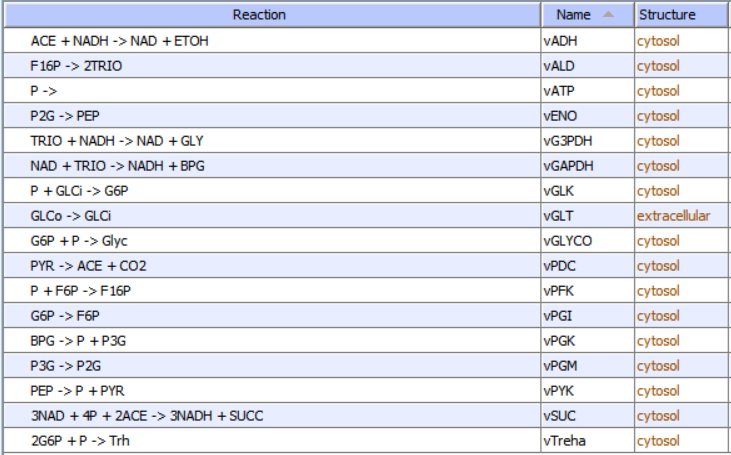
Figure \(\PageIndex{10}\): List of reactants and concentrations for yeast glycolysis. P is ATP, ACE is acetaldehyde, a reactant/product of the enzyme alcohol dehydrogenase.
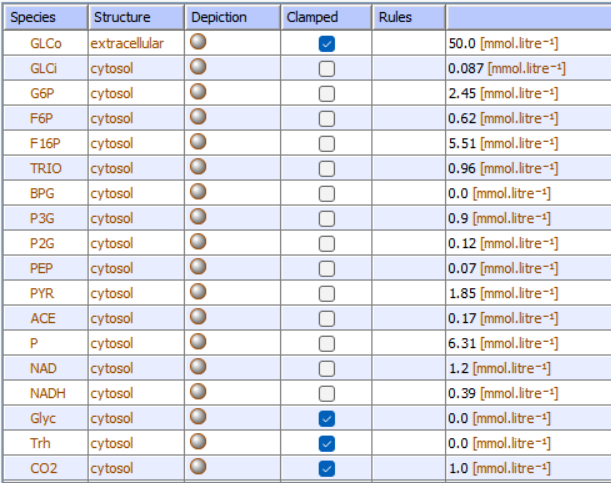
d. Parameters (concentrations, rate, enzyme kinetic, and equilibria constants) of all species. Figure \(\PageIndex{11}\) below shows the initial concentrations for the glycolysis model.
e. Equations that can be used to compute the change in concentrations of all species with time. These are usually ordinary differential equations (ODE) as described in Chapter 6B - Kinetics of Simple and Enzyme-Catalyzed Reactions, Sections B1: Single Step Reactions.) ODEs are easy to write but require a computer to solve as the number of interacting species increases.
For a quick review, consider the relatively simple reaction scheme shown in Figure \(\PageIndex{12}\) below. The set of ODEs for each species is shown below that.
This set of ODEs for each species can be written.
\begin{equation}
\begin{aligned}
\frac{d[A]}{d t} &=-k_1[A][B]+k_2[C] \\
\frac{d[B]}{d t} &=-k_1[A][B]+k_2[C] \\
\frac{d[C]}{d t} &=+k_1[A][B]-k_2[C]-k_3[C]=+k_1[A][B]-\left(k_2+k_3\right)[C] \\
\frac{d[D]}{d t} &=+k_3[C]
\end{aligned}
\end{equation}
If a reaction removes species X, the right side of the ODE for the disappearance of that species has a – sign for that term. Likewise, if a reaction increases species X, the right-hand side has a + sign. The above examples show unimolecular (C to D, C to A + B) and bimolecular (A+B to C) reactions.
Now let's look at the equations just for the change in the concentration of glucose-6-phosphate. One reaction forms it and 3 remove it, as shown in Figure \(\PageIndex{13}\) below.
Figure \(\PageIndex{13}\): The reactions that change [G6P] in the Teusink yeast glycolysis model
An ODE can be written for the change in concentration of glucose-6-phosphate.
\begin{equation}
\left.\mathrm{d}[\mathrm{G} 6 P] / \mathrm{dt}=v_{\mathrm{HK}}-v_{\mathrm{PGI}}-2 v_{\text {trehalose }}-v_{\text {glycogen }}\right)
\end{equation}
where HK is hexokinase and PGI is phosphoglucoisomerase.
Let's look at the terms more closely and how the terms are written in Vcell.
Formation of G6P
Only one reaction goes towards G6P. Its the reaction catalyzed by hexokinase (G + ATP → G6P + ADP). In the Vcell reaction diagram, ATP is represented by P. Flux J =
\begin{equation}
\frac{V m G L K \cdot\left(G L C i \cdot A T P-\frac{G 6 P \cdot A D P}{K e q G L K}\right)}{K m G L K G L C i \cdot K m G L K A T P \cdot\left(1.0+\frac{G L C i}{K m G L K G L C i}+\frac{G 6 P}{K m G L K G 6 P}\right) \cdot\left(1.0+\frac{A T P}{K m G L K A T P}+\frac{A D P}{K m G L K A D P}\right)}
\end{equation}
Removal of G6P
3 reactions go away from G6P.
i. G6P → F6P. Flux J =
\begin{equation}
\frac{V m P G I_{-} 2 \cdot\left(G 6 P-\frac{F 6 P}{K e q P G I_{-} 2}\right)}{K m P G I G 6 P_{-} 2 \cdot\left(1.0+\frac{G 6 P}{K m P G I G 6 P \_2}+\frac{F 6 P}{K m P G I F 6 P_{-}2}\right)}
\end{equation}
ii. G6P → Glycogen
Flux J = KGLYCOGEN_3
iii. G6P → Trehalose
Flux J = KTREHALOSE
Now let's run a simulation of the model of yeast glycolysis (Teusink,B et al.: Eur J Biochem 2000 Sep;267(17):5313-29). The actual model is available from Biomodels (BIOMD0000000064).
Yeast Glycolysis
For Figure \(\PageIndex{14}\) below, the model above model was run and the CSV file was used to plot the concentration vs time plots for each species. Two of the species, EtOH (50 mM) and GLCo - glucose outside (50 mM), have fixed concentrations much larger than the rest, so they are omitted from the graph for clarity. When you run the simulation above, do the same when you download the csv file and plot the progress curves. Also, note that when you run the simulation, the y-axis values are not shown correctly. Rescale them in the spreadsheet based on the correct values of EtOH and GLC0, which were held constant (clamped) throughout the time course at 50 mM.
Figure \(\PageIndex{14}\): Time course graphs of all glycolytic species vs time
How close does simulation replicate fluxes found experimentally in vivo? As mentioned above, without the additions of the branch reaction, steady state was not achieved in the simulation. Fluxes in the model were within a factor of two for only about half of the enzymes so the model needs improvement. Other discrepancies could be accounted for generically by differences in kinetics in vivo compared to in vitro measurements. Additional products (glycogen, trehalose, glycerol and succinate) were derived from glucose, which mainly entered glycolysis and was converted to ethanol, showing the complexity in modeling even a relatively "simple" pathway as glycolysis.
Metabolic Control Analysis and Simple Enzyme Inhibition
Biochemists model complex enzyme-catalyzed reactions in the presence and absence of modifiers (either activators or inhibitors) to develop mechanisms for the reactions. The following kinetic parameters are experimentally determined by fitting initial velocity (vo) vs substrate concentration ([S]) through nonlinear fitting algorithms.
- Km – the Michaelis Constant, the concentration of substrate at half-maximal velocity;
- Vm – the velocity at saturating substrate concentration;
- kcat - the turnover number for conversion of bound reactant to product;
- Kix – inhibition dissociation constants.
An example of competitive inhibition, shown in Figure \(\PageIndex{15}\), illustrates a common type of analysis for such reactions.

One modern pictorial depiction of a simple irreversible, enzyme-catalyzed reaction of substrate S going to product P with inhibition by the product and by an added inhibitor is shown in Figure \(\PageIndex{16}\). The square, a "node" in the reaction diagram, represents the enzyme.
Consider the simple enzyme-catalyzed reaction for a reversible conversion of substrate S to product P that has 3 reversible steps., as shown in Figure \(\PageIndex{17}\)

If the forward (f) and reverse (r) chemical reaction steps were irreversible and written separately, simple Michaelis-Menten equations could be written for each.
\begin{equation}
\begin{aligned}
&v_f=\frac{V_f S}{K_{M S}+S}=\frac{\frac{V_f S}{K_{M S}}}{1+\frac{S}{K_{M S}}} \\
&v_r=\frac{V_r P}{K_{M P}+P}=\frac{\frac{V_r P}{K_{M P}}}{1+\frac{P}{K_{M P}}}
\end{aligned}
\end{equation}
For the actual reversible reactions, the net forward rate cannot be found by simple subtraction of the two equations above as the differential equations describing the simple forward and reverse rates don’t account for the reverse steps
\begin{equation}
v \neq\left[\frac{\frac{V_f S}{K_{M S}}}{1+\frac{S}{K_{M S}}}-\frac{\frac{V_r P}{K_{M P}}}{1+\frac{P}{K_{M P}}}\right]
\end{equation}
A simple derivation (assuming rapid equilibrium for both forward and reverse steps) can be made for the net forward reaction. Again consider the following enzyme-catalyzed reaction (Figure 17 above):

Here it is!
- Derivation
-
You may remember that for the isolated E + S ↔ ES and for the E + P ↔ EP reactions, the simple dissociation constants, KS and KP are given by
\begin{equation}
\begin{aligned}
&K_S=\frac{E_{e q} S_{e q}}{E S_{e q}}=\frac{k_{-1}}{k_1} \text { or } E S=\frac{[E][S]}{K_S} \\
&K_P=\frac{E_{e q} P_{e q}}{E P_{e q}}=\frac{k_3}{k_{-3}} \text { or } E P=\frac{[E][P]}{K_P}
\end{aligned}
\end{equation}The rapid equilibrium assumption states that the rate of dissociation of ES and EP, which are both physical steps, is much faster than the rate of the chemical conversion steps for each complex. Hence \(k_{-1} \gg k_2\) and \(k_3 \gg k_{-2}\), so the relative amounts of ES and EP can be determined from the dissociation constants as shown above.
Mass conservation of enzymes gives
\begin{equation}
E_0=E+E S+E P=E+\frac{[E][S]}{K_S}+\frac{[E][P]}{K_p}=E\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]
\end{equation}From this, we can get the fractional amount of both ES and EP
\begin{equation}
\begin{aligned}
&\frac{E S}{E_0}=\frac{\frac{[E][S]}{K_S}}{E\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]} \text { or } E S=\frac{E_0 \frac{[S]}{K_S}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]} \\
&\frac{E P}{E_0}=\frac{[E][P]}{E\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_P}\right]} \text { or } E P=\frac{E_0 \frac{[P]}{K_P}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_P}\right]}
\end{aligned}
\end{equation}Now we can derive the rate equation for the net forward reaction for the rapid equilibrium case:
\begin{equation}
v=k_2[E S]-k_{-2}[E P]=k_2 \frac{E_0 \frac{[S]}{K_S}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}-k_{-2} \frac{E_0 \frac{[P]}{K_p}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}
\end{equation}Knowing that k2E0 and k-2E0 represent the maximal velocities, Vf and Vr, respectively, the equation becomes:
\begin{equation}
v=k_2[E S]-k_{-2}[E P]=\frac{V_f \frac{[S]}{K_S}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}-\frac{V_r \frac{[P]}{K_p}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}=\frac{V_f \frac{[S]}{K_S}-V_r \frac{[P]}{K_p}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}
\end{equation}
Here is the derived equation.
\begin{equation}
v=k_2[E S]-k_{-2}[E P]=\frac{V_f \frac{[S]}{K_S}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}-\frac{V_r \frac{[P]}{K_p}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}=\frac{V_f \frac{[S]}{K_S}-V_r \frac{[P]}{K_p}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}
\end{equation}
An equation of a similar form can be derived from the steady state assumption. Hence the net forward rate can't be determined by simple substration of the backward rate from the forward rate as shown in Equation 10 above.
Common Forms of Kinetic Equations
Programs like COPASI and VCell have many built-in equations for the velocities of many enzyme-catalyzed reactions that have similar forms. Two are shown below:
Reversible Michaelis-Menten:
\begin{equation}
\frac{\frac{V_f[\text { substrate }]}{K_{M s}}-\frac{V_r[\text { product }]}{K_{M p}}}{1+\frac{[\text { substrate }]}{K_{M s}}+\frac{[\text { product }]}{K_{M p}}}
\end{equation}
Competitive Inhibition Reversible:
\begin{equation}
\frac{\frac{V_f[\text { substrate }]}{K_{M s}}-\frac{V_r[\text { product }]}{K_{M p}}}{1+\frac{[\text { substrate }]}{K_{M s}}+\frac{[\text { product }]}{K_{M p}}+\frac{[\text { inhibitor }]}{K_I}}
\end{equation}
What is most important for readers to understand is not detailed derivations or how to solve the differential equations on their own. However, you should be able to:
- write the differential equation of a given reaction;
- recognize the common equations used for nonenzyme-catalyzed reactions (mass action) and enzyme-catalyze ones;
- change parameters in programs that use numerical methods to solve systems of linked differential equations for a system and see how the time course graphs are affected.