6.3: Kinetics with Enzymes

Search Fundamentals of Biochemistry

An enzyme alters the pathways for converting a reactant to a product by binding to the reactant and facilitating the intramolecular conversion of bound substrate to bound product before it releases the product. Enzymes do not affect the thermodynamics of reactions. For reversible reactions (as an example), the equilibrium constant, K_eq, is unchanged. What is charged is the rate at which equilibrium is achieved. Enzymes lower the activation energy for bound transition states and change the reaction mechanism.

Figure \(\PageIndex{1}\) shows the simplest chemical reaction that can be written to show how an enzyme catalyzes a reaction.

Figure \(\PageIndex{1}\): Chemcial equation for a simple enzyme-catalyzed reaction

Rapid Equilibrium Enzyme-Catalyzed Reactions

We have previously derived equations for the reversible binding of a ligand to a macromolecule. Next, we derived equations for the receptor-mediated facilitated transport of a molecule through a semipermeable membrane. This latter case extended the former case by adding a physical transport step. Now, in what hopefully will seem like deja vu, we will derive almost identical equations for the chemical transformation of a ligand, commonly referred to as a substrate, into a product by an enzyme. We will study two scenarios based on two different assumptions, each enabling a straightforward mathematical derivation of kinetic equations:

1. Rapid Equilibrium Assumption - enzyme E (macromolecule) and substrate S (ligand) concentrations can be determined using the dissociation constant since E, S, and ES are in rapid equilibrium, as we previously used in our derivation of the equations for facilitated transport. Sorry about the switch from A to S in the designation of the substrate. Biochemists use S to represent the substrate (ligand) and A, B, P, and Q to represent reactants and products in the case of multi-substrate and multi-product reactions.
2. Steady State Assumption (more general) - enzyme and substrate concentrations are not those determined using the dissociation constant.

Enzyme kinetics experiments, as we will see in the following chapters, must be used to determine the detailed mechanism of the catalyzed reaction. Using kinetic analysis, you can determine the order of binding/dissociation of substrates and products, the rate constants for individual steps, and clues to the mechanism used by the enzyme in catalysis.

Consider the following reaction mechanism for the enzyme-catalyzed conversion of substrate S into product P. (We will assume that the catalyzed rate is much greater than the noncatalyzed rate.)

\[\ce{E +S <=>[K_s] ES ->[k_3] E + P} \nonumber \]

As we did for the derivation of the equations for the facilitated transport reactions under rapid equilibrium conditions, this derivation is based on the assumption that the relative concentrations of S, E, and ES can be determined by the dissociation constant, K_S, for the interactions and the concentrations of each species during the early part of the reaction (i.e. under initial rate conditions). Assume also the S >> E₀. Remember that under these conditions, S does not change much with time. Is this a valid assumption? Examine the mechanism shown above. S binds to E with a second-order rate constant k₁. ES has two fates. It can dissociate with a first-order rate constant k₂ to S + E, or it can be converted to product with a first-order rate constant of k₃ to give P + E. If we assume that k₂ >> k₃ (i.e. that the complex falls apart much more quickly than S is converted to P), then the relative ratios of S, E, and ES can be described by Ks. Alternatively, you can think about it this way. If S binds to E, most of S will dissociate, and a small amount will be converted to P. If it does, then E is now free, and will quickly bind S and reequilibrate since the most likely fate of bound S is to dissociate, not be converted to P (since \(k_3 \ll k_2\)). This also makes sense if you consider that the physical step, characterized by k₂, is likely to be quicker than the chemical step, characterized by k₃. Hence the following assumptions have been used:

• \(S \gg E_0\)
• \(P_0 = 0\)
• \(k_3\) is rate limiting (i.e. the slow step)

We will derive equations showing the initial velocity v as a function of the initial substrate concentration, S₀, assuming that P is negligible over the time period used to measure the initial velocity. Also assume that \(v_{catalyzed} \gg v_{noncatalyzed}\). In contrast to the first-order reaction of S to P in the absence of E, v is not proportional to S₀ but rather to S_bound. Therefore, \(v \propto [ES]\), or

\[v = {const} [ES] = k_3 [ES] \label{EQ10} \]

where \(v\) is the velocity (i.e., reaction rate).

Now, let's get \(ES\) from the dissociation constant K_S (assuming rapid equilibrium of E, S and ES) and mass balance for E (E₀ = E + ES , so E = E₀ - ES). We will use mass balance for S when we derive the equation of the steady state. In many cases, S is approximately equal to S₀ or the total amount of substrate. This makes sense if you consider that the enzyme is a catalyst acts repeatedly to produce the product, so you don't need significant amounts of the enzyme. The resulting equation of [ES] is shown below.

\begin{equation}
(E S)=\frac{\left(E_0\right)(S)}{K_S+(S)}
\end{equation}

A derivation of [ES] under rapid equilibrium conditions

Here it is!

Derivation

\begin{equation}
\begin{gathered}
K_S=\frac{[E][S]}{[E S]}=\left(\frac{\left.\left(\left[E_0\right]-[E S]\right)[S]\right)}{[E S]}\right. \\
(E S) K_S=\left(E_0\right)(S)-(E S)(S) \\
(E S) K_S+(E S)(S)=\left(E_0\right)(S) \\
(E S)\left(K_S+(S)\right)=\left(E_0\right)(S)
\end{gathered}
\end{equation}

This derivation assumes that we know S (which is equal to S₀) and E_tot (which is E₀).

Let us assume that S is much greater than E, as is the likely biological case. We can calculate ES using the following equations and the same procedure we used for the derivation of the binding equation, which gives the equation below:

\begin{equation}
[E S]=\frac{\left[E_0\right][S]}{K_S+S}
\end{equation}

which is analogous to

\begin{equation}
[M L]=\frac{\left[M_0\right][S]}{K_D+L}
\end{equation}

This leads to

\begin{equation}
v_0=\frac{\left(k_3\right)\left(E_0\right)(S)}{K_S+(S)}=\frac{\left(V_M\right)(S)}{K_S+(S)}
\end{equation}

where

\begin{equation}
V_M=k_3 E_0
\end{equation}

This is the world-famous Henri-Michaelis-Menten Equation. It is a hyperbola just like the graph for binding of a ligand to a macromolecule with a given dissociation constant, K_D^.

Move the sliders in the interactive graph below to see how changing Km and Vm alters the graph. Note that this graph is identical to the graph for M + L ↔ ML.

​

Just as in the case with noncatalyzed first-order decay, it is easiest to measure the initial velocity of the reaction when [S] does not change much with time and the velocity is constant (i.e. the slope of the dP/dt curve is constant). A plot of [P] vs t (called a progress curve) is made for each different substrate concentration studied. From these curves, the initial rates at each [S] is determined.

Alternatively, one reaction time that gives a linear rise in [P] with time is determined for all the different substrate concentrations. At that specified time, the reaction can be stopped (quenched) with a reagent that does not cause any change in S or P. Then initial rates can be easily calculated for each [S] from a single data point.

Under these conditions:

• a plot of v vs S is hyperbolic
• v = 0 when S = 0
• v is a linear function of S when S<<Ks.
• v = V_max (or V_M) when S is much greater than Ks
• S = K_S when v = V_M/2.

These are the same conditions we detailed for our understanding of the binding equation

\begin{equation}
(M L)=\frac{\left(M_0\right) L}{K_D+L}
\end{equation}

Note that when S is not >> K_S, the graph does not reach saturation and does not look hyperbolic. It should be apparent from the graph that only if S >> KS (or when S is approximately 100 x > K_s) will saturation be achieved.

The K_S constant is usually called the Michaelis constant, K_M. We will see in a bit that the K_M for most enzyme-catalyzed reactions is not equal to the dissociation constant for ES, which we called K_S.

Very often, these graphs are transformed into double reciprocal or Lineweaver-Burk plots as shown below.

\begin{equation}
\frac{1}{v_0}=\frac{K_M+S}{V_M S}=\left(\frac{K_M}{V_M}\right) \frac{1}{S}+\frac{1}{V_M}
\end{equation}

These plots are used to estimate V_M from the 1/v intercept (1/V_M) and K_M from the 1/S axis (-1/K_M). These values should be used as "seed" values for a nonlinear fit to the hyperbola that models the actual v vs S curve. An interactive graph of 1/v₀ vs 1/[S] is shown below. Change the sliders for K_M and V_M and note the change in the slope and intercepts of the plot

Help

As we saw in the graph of A or P vs t for a noncatalyzed, first-order reaction, the velocity of the reaction, given as the slope of those curves, is always changing. Which velocity should we use in Equation 5? The answer invariably is the initial velocity, v₀, measured in the early part of the reaction when little substrate is depleted. Hence v vs S curves for enzyme-catalyzed reactions invariably are really v₀ vs [S] curves.

Steady State Enzyme-Catalyzed Reactions

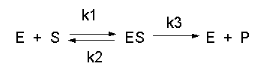
In this derivation, we will consider the following equations and all the rate constants, and will not arbitrarily assume that k₂ >> k₃. We will still assume that S >> E₀ and that P₀ = 0. An added assumption, however, is that d[ES]/dt is approximately 0. Look at this assumption this way. When an excess of S is added to E, ES is formed. In the rapid equilibrium assumption, we assumed that it would fall back to E + S (a physical step) faster than it would go onto product (a chemical step). In the steady state case, we will assume that ES might go on to product either less or more quickly than it will fall back to E + S. In either case, a steady state concentration of ES arises within a few milliseconds, and its concentration does not change significantly during the initial part of the reaction under which the initial rates are measured. Therefore, d[ES]/dt is about 0. For the rapid equilibrium derivation, v = k₃[ES]. We then solved for ES using K_S and mass balance of E. In the steady state assumption, the equation v= k₃[ES] still holds, but now we will solve for [ES] using the steady state assumption that d[ES]/dt =0.

\begin{equation}
\frac{d[E S]}{\mathrm{dt}}=\mathrm{k}_1[E][S]-\mathrm{k}_2[E S]-\mathrm{k}_3[E S]=0
\end{equation}

We can solve this and obtain the Michaelis-Menten equation for reaction.

\begin{equation}
\mathrm{v}=\mathrm{k}_3[\mathrm{ES}]=\frac{\mathrm{k}_3\left[\mathrm{E}_0\right][\mathrm{S}]}{\frac{\mathrm{k}_2+\mathrm{k}_3}{\mathrm{k}_1}+\mathrm{S}}=\frac{\mathrm{V}_{\mathrm{M}}[\mathrm{S}]}{\mathrm{K}_{\mathrm{M}}+\mathrm{S}}
\end{equation}

Derivation of the Michaelis-Menten Equation for the steady state

To see how to derive this, click below.

Answer

Applying mass balance for E (i.e E = E₀-ES) in appropriate term below gives

\begin{array}{l}{\mathrm{k}_{1}[E][S]=\left(\mathrm{k}_{2}+\mathrm{k}_{3}\right)[E S]} \\ {\mathrm{k}_{1}\left[\mathrm{E}_{0}-\mathrm{ES}\right][S]=\left(\mathrm{k}_{2}+\mathrm{k}_{3}\right)[E S]} \\ {\mathrm{k}_{1}\left[\mathrm{E}_{0}\right][S]-\mathrm{k}_{1}[\mathrm{ES}][S]=\left(\mathrm{k}_{2}+\mathrm{k}_{3}\right)[E S]} \\ {\mathrm{k}_{1}\left[\mathrm{E}_{0}\right][S]=\left(\mathrm{k}_{2}+\mathrm{k}_{3}\right)[E S]+\mathrm{k}_{1}[\mathrm{ES}][S]} \\ {\mathrm{k}_{1}\left[\mathrm{E}_{0}\right][S]=[E S]\left(\mathrm{k}_{2}+\mathrm{k}_{3}+\mathrm{k}_{1} \mathrm{S}\right)}\end{array}

Solving for [ES] gives

\begin{equation}
[\mathrm{ES}]=\left(\frac{\left[\mathrm{E}_0\right][\mathrm{S}]}{\frac{\mathrm{k}_2+\mathrm{k}_3}{\mathrm{k}_1}+\mathrm{S}}\right)
\end{equation}

Substituting into the Henri Michaelis Menten equation gives

\begin{equation}
\mathrm{v}=\mathrm{k}_3[\mathrm{ES}]=\frac{\mathrm{k}_3\left[\mathrm{E}_0\right][\mathrm{S}]}{\frac{\mathrm{k}_2+\mathrm{k}_3}{\mathrm{k}_1}+\mathrm{S}}=\frac{\mathrm{V}_{\mathrm{M}}[\mathrm{S}]}{\mathrm{K}_{\mathrm{M}}+\mathrm{S}}
\end{equation}

Note that

\begin{equation}
V_M=k_3 E_0
\end{equation}

and

\begin{equation}
K_M=\frac{k_2+k_3}{k_1}
\end{equation}

Now let's look at a progress curve simulation that compares the Michaelis-Menten equation derived from rapid equilibrium assumptions (when k₂>>k₃) and in which K_M is the actual dissociation constant to the steady state approximation, when k₂ is not >>k₃.  Reaction 1 is the rapid equilibrium and Reaction 2 the steady state.

---

MODEL

A comparison of the rapid equilibrium (left) and steady state (right)Michaels-Menten reaction

\begin{equation} v_0=\frac{k_3\left[E_O\right][S]}{K_M+S}=\frac{V_M[S]}{K_M+S} \end{equation}	\begin{equation} v_0=\frac{k_3\left[E_O\right][S]}{\frac{k_2+k_3}{k_1}+S}=\frac{V_M[S]}{K_M+S} \end{equation}
Initial Condition:  VM = 10  ; KM = 10;  S = 50	Initial Conditions: k1 = 10  ; k2 = 90 ;  k3 = 10 ;  E0 = 1 uM; S = 50 VM = k3E0 =10;   KM = (k2 + k3)/k2 = 10)

Select Load [model name] below

 Select Start to begin the simulation.

Interactive Element

Select Plot to change Y axis min/max, then Reset and Play  |  Select Slider to change which constants are displayed |  Select About  for software information.

Move the sliders to change the constants and see changes in the displayed graph in real-time.

Time course model made using Virtual Cell (Vcell), The Center for Cell Analysis & Modeling, at UConn Health.  Funded by NIH/NIGMS (R24 GM137787); Web simulation software (miniSidewinder) from Bartholomew Jardine and Herbert M. Sauro, University of Washington.  Funded by NIH/NIGMS (RO1-GM123032-04)

---

 

The initial conditions in the graph are set so the graphs of the rapid equilibrium and steady state are identical.

Recommendations:

• Scale the y-axis to 50
• change the slider k_{2_r2} for the steady state graph to other values. Watch the curves separate. Although these plots are only for 1 substrate concentration (50 uM), the effects of changing k₂ for the steady state plot are very dramatic. This should convince you that in general, unless k₃ << k₂, the calculated value of K_M is not equal to the thermodynamic dissociation constant, K_D.

Analysis of the General Michaelis-Menten Equation

This equation can be simplified and studied under different conditions. First, notice that (k₂ + k₃)/k₁ is a constant which is a function of relevant rate constants. This term is usually replaced by K_M which is called the Michaelis constant. Likewise, when S approaches infinity (i.e. S >> K_M, equation 5 becomes v = k₃(E₀) which is also a constant, called V_M for maximal velocity. Substituting V_M and K_M into equation 5 gives the simplified equation:

\begin{equation}
\mathrm{v}=\frac{\mathrm{V}_{\mathrm{M}}[\mathrm{S}]}{\mathrm{K}_{\mathrm{M}}+\mathrm{S}}
\end{equation}

It is extremely important to note that K_M in the general equation does not equal the K_S, the dissociation constant used in the rapid equilibrium assumption! K_M and K_S have the same units of molarity, however. A closer examination of K_M shows that under the limiting case when k₂ >> k₃ (the rapid equilibrium assumption) then,

\begin{equation}
\mathrm{K}_{\mathrm{M}}=\frac{\mathrm{k}_2+\mathrm{k}_3}{\mathrm{k}_1}=\frac{\mathrm{k}_2}{\mathrm{k}_1}=\mathrm{K}_{\mathrm{D}}=\mathrm{K}_{\mathrm{S}}
\end{equation}

If we examine these equations under several different scenarios, we can better understand the equation and the kinetic parameters:

• when S = 0, v = 0.
• when S >> K_M, v = V_M = k₃E₀. (i.e. v is zero order with respect to S and first order in E. Remember, k₃ has units of s^-1> since it is a first-order rate constant. k₃ is often called the turnover number, because it describes how many molecules of S "turn over" to product per second.
• v = V_M2, when S = K_M.
• when S << K_M, v = V_MS/K_M = k₃E₀S/K_M (i.e. the reaction is bimolecular, dependent on both on S and E. k3/K_M has units of M^-1s^-1, the same as a second order rate constant.

More Complicated Enzyme-catalyzed Reactions

A reversibly-catalyzed reaction

You have learned previously that enzymes don't change the equilibrium constant for a reaction, but rather lowers the activation energy barrier to move from reactants to products. This implies that the activation energy to move in the reverse direction, from products to reactants, is also lowered. Hence the enzyme speeds up both the forward and reverse reaction. We haven't accounted for that yet in our kinetic equations. Many reactions in metabolic reactions that do not have large negative values of ΔG (ie. they are not significantly favored) are reversible, allowing the enzyme to be used in the reverse direction. Take for example the pathway to break down glucose to pyruvate (glycolysis). It has 9 different steps, of which 5 are reversible, allowing them to be used in the reverse pathway to take pyruvate to glucose (gluconeogenesis).

Let's set up the equations for the reversible reaction of substrate S to product P catalyzed by enzyme E. Assume that the K_M for the forward reaction is K_MS (or K_S) and for the reverse reaction is K_MP (or K_P) as shown in the reaction scheme in Figure \(\PageIndex{2}\). The rate constant k₂ is the k_cat (forward rate constant) for conversion of ES to EP and k_-2 is the k_cat (reverse rate constant) for conversion of EP to ES

Figure \(\PageIndex{2}\): Reaction scheme for a simple enzyme-catalyzed reaction

The following simple Michaelis-Menten equations can be written for just the forward reaction and for the reverse reaction:

\begin{equation}
\begin{aligned}
&v_f=\frac{V_f S}{K_{M S}+S}=\frac{\frac{V_f S}{K_{M S}}}{1+\frac{S}{K_{M S}}} \\
&v_r=\frac{V_r P}{K_{M P}+P}=\frac{\frac{V_r P}{K_{M P}}}{1+\frac{P}{K_{M P}}}
\end{aligned}
\end{equation}

Now you might think that simply substracting the two would give the net velocity in the forward direction, but that is NOT the case.

\begin{equation}
v \neq\left[\frac{\frac{V_f S}{K_{M S}}}{1+\frac{S}{K_{M S}}}-\frac{\frac{V_r P}{K_{M P}}}{1+\frac{P}{K_{M P}}}\right]
\end{equation}

The reason is that in the derivation, the equations for both the forward and reverse rates must have terms for the reverse and forward reactions, respectively.

A simple derivation shows that this is the equation for the reversible conversion of substrate to product.

\begin{equation}
v=k_2[E S]-k_{-2}[E P]=\frac{V_f \frac{[S]}{K_S}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_p}\right]}-\frac{V_r \frac{[P]}{K_P}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_P}\right]}=\frac{V_f \frac{[S]}{K_S}-V_r \frac{[P]}{K_P}}{\left[1+\frac{[S]}{K_S}+\frac{[P]}{K_P}\right]}
\end{equation}

This reversible form of the Michaelis-Menten equation and other equations, written in the format shown in equation 6.24, are commonly used in programs such as VCell and Copasi to model the kinetics of whole pathways of biological interactions and reactions. The figures below show a reaction diagram, graphical results showing S and P vs time for the selected K_M and V_M values shown, and animations for the reaction. The chemical (S and P) are shown as green spheres connected by a line. The red dot again represents the enzyme (shown as a node of connection between S and P). Equation 6.24 was used to model the reversible reaction (even though the arrows shown between S and P are unidirectional.

---

MODEL

Reversible Enzyme-Catalyzed Reaction:   E + S  ↔  ES  ↔  EP  ↔ E  + P .

Vcell reaction diagram (1-way arrows defined as reversible in the actual mathematical model) and chemical equation

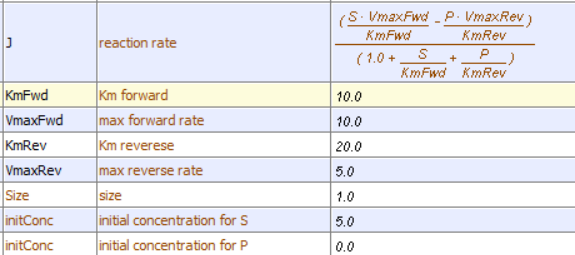
Initial parameter values: as shown in above

Select Load [Enz Rev] below

 Select Start to begin the simulation.

Interactive Element

Select Plot to change Y axis min/max, then Reset and Play  |  Select Slider to change which constants are displayed |  Select About  for software information.

Move the sliders to change the constants and see changes in the displayed graph in real-time.

Time course model made using Virtual Cell (Vcell), The Center for Cell Analysis & Modeling, at UConn Health.  Funded by NIH/NIGMS (R24 GM137787); Web simulation software (miniSidewinder) from Bartholomew Jardine and Herbert M. Sauro, University of Washington.  Funded by NIH/NIGMS (RO1-GM123032-04)

---

 

If you reflect on it, this reaction is very similar to the reversible reaction of A ↔ P in the absence of an enzyme, which we explored in Chapter section 6.2. Just for comparison, the graph for that reaction is shown below. Change the sliders to produce a curve similar to the enzyme-catalyzed reaction shown in the figure above.

Reaction with intermediates

Not all reactions can be characterized so simply as a simple substrate interacting with an enzyme to form an ES complex, which then turns over to form product. Sometimes, intermediates form. For example, a substrate S might interact with E to form a complex, which then is cleaved to products P and Q. Q is released from the enzyme, but P might stay covalently attached. This happens often in the hydrolytic cleavage of a peptide bond by a protease, when an activated nucleophile like Ser reacts with the sessile peptide bond in a nucleophilic substitution reaction, releasing the amine end of the former peptide bond as the leaving group while the carboxy end of the peptide bond remains bonded to the Ser as an Ser-acyl intermediate. Water then enters and cleaves the acyl intermediate, freeing the carboxyl end of the original peptide bond. This is shown in the written reaction in Figure \(\PageIndex{3}\):

Figure \(\PageIndex{3}\): Reaction scheme for enzyme-catalyzed reaction with an intermediate

Even for this seemingly complicated reaction, you get the standard Michaelis-Menten equation.

To simplify the derivation of the kinetic equation, let's assume that E, S, and ES are in rapid equilibrium defined by the dissociation constant, Ks. Assume Q has a visible absorbance, so it is easy to monitor. Assume from the steady state assumption that:

\begin{equation}
\frac{\mathrm{d}[\mathrm{E}-\mathrm{P}]}{\mathrm{dt}}=\mathrm{k}_2[\mathrm{ES}]-\mathrm{k}_3[\mathrm{E}-\mathrm{P}]=0
\end{equation}

assuming that k₃ is a pseudo first-order rate constant and that [H₂O] doesn't change.

The velocity depends on which step is rate-limiting. If k₃<<k₂, then the k₃ step is rate-limiting. Then

\begin{equation}
\mathrm{v}=\mathrm{k}_3[\mathrm{E}-\mathrm{P}]
\end{equation}

If k₂<<k₃, then the k₂ step is rate-limiting. Then

\begin{equation}
\mathrm{v}=\mathrm{k}_2[\mathrm{ES}]
\end{equation}

The following kinetic equation for this reaction can be derived, assuming v = k₂[ES].

\begin{equation}
\mathrm{v}=\frac{\frac{\mathrm{k}_2 \mathrm{k}_3}{\mathrm{k}_2+\mathrm{k}_3}\left[\mathrm{E}_0\right][\mathrm{S}]}{\left(\frac{\mathrm{k}_3}{\mathrm{k}_2+\mathrm{k}_3}\right) \mathrm{K}_{\mathrm{S}}+\mathrm{S}}=\frac{\mathrm{k}_{\mathrm{cat}}\left[\mathrm{E}_0\right][\mathrm{S}]}{\mathrm{K}_{\mathrm{M}}+\mathrm{S}}=\frac{\mathrm{V}_{\mathrm{M}} \mathrm{S}}{\mathrm{K}_{\mathrm{M}}+\mathrm{S}}
\end{equation}

You can verify that you get the same equation if you assume that v = k₃[E-P].

This equation looks quite complicated, especially if you substitute for Ks, k_-1/k₁. All the kinetic constants can be expressed as functions of the individual rate constants. However, this equation can be simplified by realizing the following:

• When \(\mathrm{S}>>\frac{\mathrm{K}_{\mathrm{S}} \mathrm{k}_{3}}{\mathrm{k}_{2}+\mathrm{k}_{3}}, \mathrm{v}=\left(\frac{\mathrm{k}_{2} \mathrm{k}_{3}}{\mathrm{k}_{2}+\mathrm{k}_{3}}\right) \mathrm{E}_{0}=\mathrm{V}_{\mathrm{M}}\)
• \(\frac{\mathrm{K}_{\mathrm{S}} \mathrm{k}_{3}}{\mathrm{k}_{2}+\mathrm{k}_{3}}=\mathrm{constant}=\mathrm{K}_{\mathrm{M}}\)

Substituting these into equation 7 gives:

\[\mathrm{v}=\frac{\mathrm{V}_{\mathrm{M}} \mathrm{S}}{\mathrm{K}_{\mathrm{M}}+\mathrm{S}} \nonumber \]

This again is the general form of the Michaelis-Menten equation

The expression for V_M in the first bulleted expression above is more complicated than our earlier definition of V_M = k₃E₀. They are similar in that the term E₀ is multiplied by a constant which is itself a function of rate constant(s). The rate constants are generally lumped together into a generic constant called k_cat.

• For the simple reaction k_cat = k3
• For the more complicated reaction above with a covalent intermediate, \(\mathrm{k}_{\mathrm{cat}}=\frac{\mathrm{k}_{2} \mathrm{k}_{3}}{\mathrm{k}_{2}+\mathrm{k}_{3}}\)
• For all reactions, V_M = k_catE₀.

Recent Updates (2/7/24):   Here is a VCell computational model for a bisubsrate and biproduct (BiBi) reaction with a covalent intermediate (ping pong reaction).

---

MODEL

BiBi-Ping Pong_Covalent Intermediate Irreversible reaction

Vcell reaction diagram (1-way arrows defined as reversible in actual mathematical model) and chemical equation

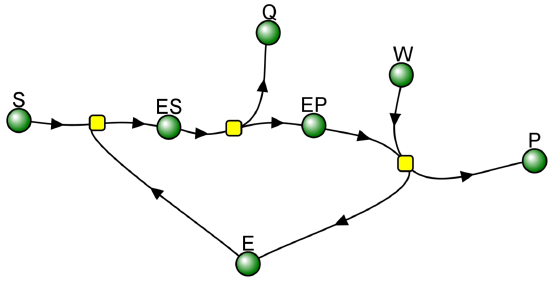
Yellow dots: Reaction Nodes (R1, R2 and R3 left to right)

Reaction made irreversible since k_r2 = 0, k_r3 = 0.

Initial parameter values:

• S₀ = 100, E₀ = 1, W (water in a hydrolysis reaction) = 50 and fixed throughout
• k_1f = 5, k_1r = 1, k_2f = 0.6,
• k_2f = 50, k_2r = 0
• k_3f = 0.05, k_3f = 0

Select Load [model name] below

 Select Start to begin the simulation.

1Interactive Element

Select Plot to change Y axis min/max, then Reset and Play  |  Select Slider to change which constants are displayed |  Select About  for software information.

To see the burst phase for reaction, change the time and parameters to these values:

• set Run time to 0.3
• Select Plot then Update Y axis max to 2
• Click Edit Plot Species and check just P and Q
• reset

Time course model made using Virtual Cell (Vcell), The Center for Cell Analysis & Modeling, at UConn Health.  Funded by NIH/NIGMS (R24 GM137787); Web simulation software (miniSidewinder) from Bartholomew Jardine and Herbert M. Sauro, University of Washington.  Funded by NIH/NIGMS (RO1-GM123032-04)

---

 

In the case when k₂ >> k₃, Q forms quickly in a burst phase due to a high k₂.  This phase is followed by the slower conversion of the accumulated EP to E + P in a steady state phase, as shown in Figure \(\PageIndex{4}\) below.  Make sure to change the parameters in the model above to best see the burst phase for production of product Q.  This reaction is an example of a BiBi (two substrates, two products) Ping Pong reaction, since 1 reactant binds, followed by 1 product departing before the second react binds and the second product departs.

Figure \(\PageIndex{4}\): Burst and steady-state phase in an enzyme-catalyzed reaction with a covalent intermediate and k₂ >> k₃. 

Reverse the rate constants in the model to k₂ = 5 and  k₃ = 0.5 so that  k₂ is not >> k₃ and note that the burst phase for Q disappears!

When plotting v₀ vs S Michaelis-Menten plots of this type of reaction, the state state v₀ should be used and NOT (v₀) _t=0 = (dQ/dt) _t=0, since that rate changes very quickly after the initial burst formation of Q.

Summary

Figure \(\PageIndex{5}\) compares the Michaelis-Menten kinetic equations for the rapid equilibrium, steady state assumptions, and covalent intermediate cases .

Figure \(\PageIndex{5}\): Michaelis-Menten kinetic equations for the rapid equilibrium, steady state assumptions, and covalent intermediate cases

Meaning of Kinetic Constants

It is important to get a "gut-level" understanding of the significance of the rate constants. Here they are:

• K_M: The Michaelis constant with units of molarity (M), is operationally defined as the substrate concentration at which the initial velocity is half of V_M. It is equal to the dissociation constant of E and S only in if E, S and ES are in rapid equilibrium. It can be thought of as an "effective" (but not actual) K_D in other cases.
• k_cat: The catalytic rate constants, with units of s^-1 is often called the turnover number. It is a measure of how many bound substrate molecules "turnover" or form product in 1 second. This is evident from equation v₀ = k_cat[ES]
• k_cat/K_M: Under condition when [S] << K_M, the Michaelis-Menten equation becomes v₀ = (k_cat/K_M)[E₀][S]. This really describes a biomolecular rate constant (k_cat/K_M), with units of M^-1s^-1, for conversion of free substrate to product. Some enzymes have k_cat/Km values around 10⁸, indicating that they are diffusion controlled. That implies that the reaction is essentially done as soon as the enzyme and substrate collide. The constant k_cat/Km is also referred to as the specificity constant in that it describes how well an enzyme can differentiate between two different competing substrates. (We will show this mathematically in the next chapter.)

Table \(\PageIndex{1}\) below shows K_M and k_cat values for various enzymes

KM values
enzyme	substrate	Km (mM)
catalase	H2O2	25
hexokinase (brain)	ATP	0.4
	D-Glucose	0.05
	D-Fructose	1.5
carbonic anhydrase	HCO3^-	9
chymotrypsin	glycyltyrosinylglycine	108
	N-benzoyltyrosinamide	2.5
b-galactosidase	D-lactose	4.0
threonine dehydratase	L-Thr	5.0
kcat values
enzyme	substrate	kcat (s^-1)
catalase	H2O2	40,000,000
carbonic anhydrase	HCO3^-	400,000
acetylcholinesterase	acetylcholine	140,000
b-lactamase	benzylpenicillin	2,000
fumarase	fumarate	800
RecA protein (ATPase)	ATP	0.4

Table \(\PageIndex{1}\): K_M and k_cat values for various enzymes

Table \(\PageIndex{2}\) below show k_cat, K_M and k_cat/K_M values for diffusion-controlled enzymes

Enzymes with kcat/KM values close to diffusion controlled (10^8 - 10^9 M^-1s^-1)
enzyme	substrate		kcat (s^-1)	Km (M)	kcat/Km (M^-1s^-1)
acetylcholinesterase	acetylcholine		1.4 x 10^4	9 x 10^-5	1.6 x 10^8
carbonic anhydrase	CO2		1 x 10^6	1.2 x 10^-2	8.3 x 10^7
	HCO3^-		4 x 10^5	2.6 x 10-2	1.5 x 10^7
catalase	H2O2		4 x 10^7	1.1	4 x 10^7
crotonase	crotonyl-CoA		5.7 x 10^3	2 x 10^-5	2.8 x 10^8
fumarase	fumarate		8 x 10^2	5 x 10^-6	1.6 x 10^8
	malate		9 x 10^2	2.5 x 10^-5	3.6 x 10^7
triose phosphate isomerase	glyceraldehyde-3-P		4.3 x 10^3	4.7 x 10^-4	2.4 x 10^8
b-lactamase	benzylpenicillin		2.0 x 10^3	2 x 10^-4	1 x 10^8

Table \(\PageIndex{2}\) below show k_cat, K_M and k_cat/K_M values for diffusion controlled enzymes

Experimental Determination of V_M and K_M

How can V_M and K_M be determined from experimental data?

From initial rate data

The most common way to determine V_M and K_M is through initial rates, v₀, obtained from P or S vs time curves. Hyperbolic graphs of v₀ vs [S] can be fitted or transformed as we explored with the different mathematical transformations of the hyperbolic binding equation to determine K_D. These included:

• Michaelis-Menten plot: nonlinear hyperbolic fit
• Lineweaver-Burk double reciprocal plot
• Scatchard plot
• Eadie-Hofstee plot

We discussed all of these plots except for the Eadie-Hofstee plot, in the chapter on binding. The Eadie-Hofstee plot is another linearized version of Michaelis-Menten equation

Here is a derivation of that equation, which starts with each side of the double-reciprocal plot being multiplied by v₀V_M.

\begin{equation}
\begin{aligned}
\left(v_0 V_M\right) \frac{1}{v_0} &=\left(v_0 V_M\right)\left(\frac{K_M}{V_M}\right) \frac{1}{S}+\left(v_0 V_M\right) \frac{1}{V_M} \\
V_M &=\left(v_0\right) K_M \frac{1}{S}+\left(v_0\right) \\
v_0 &=-K_M\left(\frac{v_0}{S}\right)+V_M
\end{aligned}
\end{equation}

Note that a graph of v₀ vs v₀/S is linear so slopes and intercepts can be used to obtain values for V_M and K_M.

The double-reciprocal plot is commonly used to analyze initial velocity vs substrate concentration data. When used for such purposes, the graphs are referred to as Lineweaver-Burk plots, where plots of 1/v vs 1/S are straight lines with slope m = K_M/V_M, and y-intercept b = 1/V_M. Figure \(\PageIndex{6}\) common graphs used to display initial rate enzyme kinetic data.

Figure \(\PageIndex{6}\): Common graphs used to display initial rate enzyme kinetic data

The straight-line plots shown above should not be analyzed using linear regression, since simple linear regression assumes constant error in v₀ values. A weighted linear regression or even better, a nonlinear fit to a hyperbolic equation should be used. (Common Error in Biochemistry Textbooks: The Shape of the Hyperbola). A rearrangement of the corresponding Scatchard equations in the Eadie-Hofstee plot is also commonly used, especially to visualize enzyme inhibition data as we will see in the next chapter.

An Extension: k_cat and V_M from integrated rate equations

K_M and V_M could be theoretically extracted from progress curves of A or P as a function of t at one single A concentration by deriving an integrated rate equation for A or P as a function of t, as we did in equation 2 (the integrated rate equation for the conversion of A → P in the absence of enzyme). In principle, this method would be better than the initial rates methods. Why? It is not easy to be certain you are measuring the initial rate for each and every [S] which should vary over a wide range. It's also time intensive. In addition, think how much data is discarded if you take an entire progress curve at each substrate concentration, especially if you quench the reaction at a given time point, which effectively limits the data to one time point per substrate.

In practice, the mathematics is complicated and it is not possible to get a simple explicit function of [P] or [S] as a function of time. A slight variant of a progress curve can be derived. Let us consider the simple case of a single substrate S (or A) being converted to product P in an enzyme-catalyzed reaction. The analogous equations for first-order, noncatalyzed rates were A=A₀e^-k₁t or P = A₀(1-e^-k₁t).

We can derive the equation for the enzyme-catalyzed reaction shown below.

Here it is!

\begin{equation}
\frac{\mathrm{P}}{\mathrm{t}}=\frac{\mathrm{K}_{\mathrm{M}} \ln \left(\frac{\mathrm{S}_0-\mathrm{P}}{\mathrm{S}_0}\right)}{\mathrm{t}}+\mathrm{V}_{\mathrm{M}}
\end{equation}

Derivation: k_cat and V_M from integrated rate equation

Click below to see the derivation

Derivation

\begin{equation}
\begin{array}{r}
\mathrm{v}=-\frac{\mathrm{dS}}{\mathrm{dt}}=+\frac{\mathrm{dP}}{\mathrm{dt}}=\frac{\mathrm{V}_{\mathrm{M}} \mathrm{S}}{\mathrm{K}_{\mathrm{M}}+\mathrm{S}} \\
\int_{\mathrm{S}_0}^{\mathrm{S}} \frac{\mathrm{K}_{\mathrm{M}}+\mathrm{S}}{\mathrm{V}_{\mathrm{M}} \mathrm{S}} \mathrm{d} S=-\int_0^{\mathrm{t}} \mathrm{t}
\end{array}
\end{equation}

\begin{equation}
-\mathrm{t}=\frac{\mathrm{S}+\mathrm{K}_{\mathrm{M}} \ln \mathrm{S}-\mathrm{S}_0-\mathrm{K}_{\mathrm{M}} \ln S_0}{\mathrm{~V}_{\mathrm{M}}}
\end{equation}

On rearrangement, this gives:

\begin{equation}
\mathrm{S}_0-\mathrm{S}+\mathrm{K}_{\mathrm{M}} \ln \frac{\mathrm{S}_0}{\mathrm{~S}}=\mathrm{V}_{\mathrm{M}} \mathrm{t}
\end{equation}

This equation is an implicit equation, not an explicit one, as it does NOT give S(t) explicitly as a function of t.

Equation yy can be written with respect to product P as follows:

\begin{equation}
\begin{aligned}
&P=\mathrm{S}_0-S{ }^{\prime \prime} \text { or }{ }^{\prime \prime} S=\mathrm{S}_0-P \\
&\mathrm{~S}_0-\left(\mathrm{S}_0-\mathrm{P}\right)+\mathrm{K}_{\mathrm{M}} \ln \frac{\mathrm{S}_0}{\mathrm{~S}_0-\mathrm{P}}=\mathrm{V}_{\mathrm{M}} \mathrm{t} \\
&\mathrm{P}-\mathrm{K}_{\mathrm{M}} \ln \left(\frac{\mathrm{S}_0-\mathrm{P}}{\mathrm{S}_0}\right)=\mathrm{V}_{\mathrm{M}} \mathrm{t}
\end{aligned}
\end{equation}

Rearranging this gives

\begin{equation}
\frac{\mathrm{P}}{\mathrm{t}}=\frac{\mathrm{K}_{\mathrm{M}} \ln \left(\frac{\mathrm{S}_0-\mathrm{P}}{\mathrm{S}_0}\right)}{\mathrm{t}}+\mathrm{V}_{\mathrm{M}}
\end{equation}

S(t) explicitly as a function of t.

This equation does not give P(t) explicitly as a function of time. Rather one can get a graph of P/t vs [ln (1-P/S₀)]/t (shown below) from the derived equation, which does give a straight line with a slope of Km and a y-intercept of Vm. Note that the calculated values of V_M and K_M are derived from only one substrate concentration, and the values may be affected by product inhibition.

Figure \(\PageIndex{7}\) shows the comparison of a first-order noncatalyzed conversion of A → P to the enzyme-catalyzed rate. The V_M for the enzyme-catalyzed reaction was chosen to be small to make the two graph comparable.

Figure \(\PageIndex{7}\): Comparison of a first order noncatalyzed conversion of A → P to the enzyme catalyzed rate

Note that the curves are similar but not identical. If you didn't know an enzyme was present, you could fit the data to a first-order rise in [P] with time, but it would not be the optimal fit. The progress curves are a lot more complicated to analyze if the product, which shares structural similarities with the substrate, binds the enzyme tightly and inhibits it (called product inhibition).

Comparison of progress Curves of uncatalyzed and catalyzed reactions.

Let's explore progress curves for enzyme-catalyzed reactions a bit further. Students usually see v₀ vs [S] Michaelis-Menten plots in textbooks. These plots are in some ways less intuitive than seeing P vs t curves, which are more in line with how we might contemplate how a reaction proceeds. Hence, it would be illuminating to compare progress curve graphs of A → P (irreversible) for the uncatalyzed and S → P for the enzyme-catalyzed reactions. What might you expect? We saw one example in Figure \(\PageIndex{6}\).

In each case, P should increase with time. In the uncatalyzed reaction, S exponentially decreases to 0 and P concomitantly rises to a value of P = S₀. You also get a rise in P vs t for the enzyme-catalyzed rate, but you would think it would be a faster rise with time since the enzyme catalyze the reaction. Figure \(\PageIndex{87}\) shows a comparison of the progress curves for the uncatalyzed first-order reaction of A → P₁ (red) and S → P₂ (blue) for enzym- catalyzed reaction (blue, right) for these conditions: uncatalyzed reaction A → P₁, k₁ = 0.1; Catalyzed reaction: S → P₂, V_M=10, K_M=5. Note that the rate at which bound S (i.e ES) goes to P for the catalyzed rate is 100x faster than the rate constant for the catalyzed rate.

Figure \(\PageIndex{8}\): Another comparison of progress curves (P vs t) for a catalyzed and uncatalyzed conversion of A → P.

Note that the curves are somewhat similar in shape but also clearly different in comparison to the one shown in Figure \(\PageIndex{6}\).

Now let's use Vcell to compare the reactions for different values for the kinetic constants for the uncatalyzed and the enzyme-catalyzed reaction. Change the constants and try to find a set of conditions so that the catalyzed and catalyzed rates for conversion of reactions to products are superimposable. How can that be?

---

MODEL

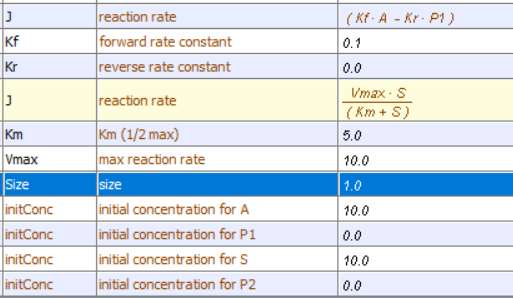
Irreversible reactions:  A → P1  and E + S ↔ ES → E + P 

Vcell reaction diagram (1-way arrows defined as reversible in actual mathematical model) and chemical equation

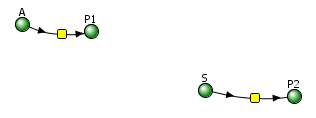
Initial conditions

Select Load [model name] below

 Select Start to begin the simulation.

Interactive Element

Select Plot to change Y axis min/max, then Reset and Play  |  Select Slider to change which constants are displayed |  Select About  for software information.

Move the sliders to change the constants and see changes in the displayed graph in real-time.

Time course model made using Virtual Cell (Vcell), The Center for Cell Analysis & Modeling, at UConn Health.  Funded by NIH/NIGMS (R24 GM137787); Web simulation software (miniSidewinder) from Bartholomew Jardine and Herbert M. Sauro, University of Washington.  Funded by NIH/NIGMS (RO1-GM123032-04)

---

 

Animations

Now let's look at an animation of the same irreversible reactions in which enzyme-catalyzed reaction is no faster than the noncatalyzed rate (a worthless enzyme!). Here are the reactions:

A→P, k₁ =0.1; S → P, V_M=?, K_M = ?.

The animations show just the accumulation of product. Animations are by Shraddha Nakak and Hui Liu.

Exercise \(\PageIndex{1}\)

Use the Vcell model above to find a set of values for K_M and V_M that would make the two graphs superimposable - i.e. when the graphs in the absence and presence of E are identical. (Hint: that would be a really bad enzyme if it didn't increase the reaction over the uncatalyzed rate!)

Answer

K_M = 96, V_M = 10