4.7: Performance Objectives

Last updated
Save as PDF

Page ID: 123044

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

After completing this lab, the student will be able to perform the following objectives:

DISCUSSION

1. State the formula for determining the number of CFUs per ml of sample when using the plate count technique.

2. When given a diagram of a plate count dilution and the number of colonies on the resulting plates, choose the correct plate for counting, determine the dilution factor of that plate, and calculate the number of CFUs per ml in the original sample.

Plate count practice problems

Exercise \(\PageIndex{1}\)

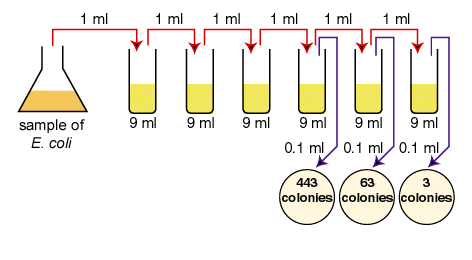
A sample of E.coli is diluted according to the above diagram. The number of colonies that grew is indicated on the petri plates. How many CFUs are there per ml in the original sample?

Answer

The correct dilutions are shown on the tubes and plates above.

The formula to be used is:

the number of CFUs per ml of sample = the number of colonies (30-300) X the dilution factor of the plate counted

First choose the correct plate to count, that is, one having between 30 and 300 colonies.

The correct plate is the one having 63 colonies on the 1/1,000,000 or 10^-6 dilution. (6.3 X 10¹ in scientific notation.)

Multiply 63 by the dilution factor of that plate.

Since the dilution factor is 1/1,000,000 or 10^-6, the dilution factor or inverse is 1,000,000 or 10⁶.
63 X 1,000,000 = 63,000,000 CFUs per ml. (6.3 X 10¹ X 10⁶ = 6.3 X 10⁷ in scientific notation.)

Exercise \(\PageIndex{2}\)

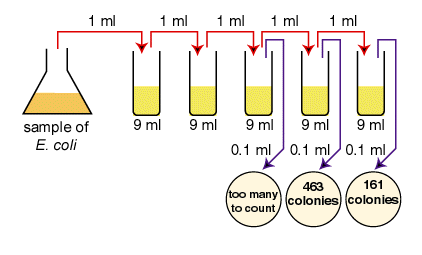
A sample of E.coli is diluted according to the above diagram. The number of colonies that grew is indicated on the petri plates. How many CFUs are there per ml in the original sample?

Answer

The correct dilutions are shown on the tubes and plates above. The formula to be used is:

the number of CFUs per ml of sample = the number of colonies (30-300) X the dilution factor of the plate counted

First choose the correct plate to count, that is, one having between 30 and 300 colonies.

The correct plate is the one having 161 colonies on the 1/1,000,000 or 10^-6 dilution. (1.61 X 10² in scientific notation.)

Multiply 161 by the dilution factor of that plate.

Since the dilution factor is 1/1,000,000 or 10^-6, the dilution factor or inverse is 1,000,000 or 10⁶.
161 X 1,000,000 =161,000,000 CFUs per ml. (1.61 X 10² X 10⁶ = 1.61 X 10⁸ in scientific notation.)

3. State the principle behind the direct microscopic method of enumeration.

4. State the formula for determining the number of bacteria per cc of sample when using the direct microscopic method of enumeration.

5. When given the total number of bacteria counted in a Petroff-Hausser chamber, the total number of large squares counted, and the dilution of the bacteria placed in the chamber, calculate the total number of bacteria per cc in the original sample

Exercise \(\PageIndex{3}\)

One ml of E.coli is mixed with 3ml of dye. A drop of this dilution is placed on a Petroff-Hausser counting chamber. Five large, double-lined squares, each containing a volume of 1/1,250,000 cc, are counted giving the following results: 46, 50, 54, 58, and 52 bacteria. How many bacteria are there per cc in the original sample?

Answer

Formula to be used:

the number of bacteria per cc =the average number of bacteria per large, double-lined square X the dilution factor of the large square (1,250,000 or 1.25 X 10 ⁶) X the dilution factor of any dilutions made prior to placing the sample in the counting chamber, e.g., mixing the bacteria with dye

First find the average number of bacteria per square by adding the 5 numbers and dividing by 5.

46+50+54+58+52 = 260.
260 divided by 5 = 52. There is an average of 52 bacteria per square. (5.2 X 10¹ in scientific notation.)

Multiply 52 times the dilution factor of the square which is always 1,250,000. (The square holds 1/1,250,000 of a cc. The dilution factor or inverse of 1/1,250,000 is 1,250,000/1.)

52 X 1,250,000 = 65,000,000. (5.2 X 10¹ X 1.25 X 10⁶ = 6.5 X 10⁷ in scientific notation.)

Now multiply that number by the dilution factor of the dilution made when the bacteria was mixed with dye.

One ml of bacter was mixed with 3ml of dye. This is a 1/4 dilution. The dilution factor or inverse of 1/4 is 4/1.
65,000,000 X 4 = 260,000,000. (6.5 X 10⁷ X 4 = 2.6 X 10⁸ in scientific notation.)
There are 260,000,000 E. coli per cc in the original sample. (In scientific notation, the answer would be 2.6 X 10⁸.)

Exercise \(\PageIndex{4}\)

One ml of E.coli is mixed with 1ml of dye. A drop of this dilution is placed on a Petroff-Hausser counting chamber. Five large, double-lined squares, each containing a volume of 1/1,250,0000 cc, are counted giving the following results: 61, 74, 78, 63 and 64 bacteria. How many bacteria are there per cc in the original sample?

Answer

Formula to be used:

the number of bacter per cc = the average number of bacteria per large, double-lined square X the dilution factor of the large square (1,250,000 or 1.25 X 10⁶) X the dilution factor of any dilutions made prior to placing the sample in the counting chamber, e.g., mixing the bacteria with dye

First find the average number of bacteria per square by adding the 5 numbers and dividing by 5.

61+74+78+63+64 = 340
340 divided by 5 = 68. There is an average of 68 bacteria per square. (6.8 X 10¹ in scientific notation.)

Multiply 68 times the dilution factor of the square which is always 1,250,000. (The square holds 1/1,250,000 of a cc. The dilution factor or inverse of 1/1,250,000 is 1,250,000/1.)

68 X 1,250,000 = 85,000,000. (6.8 X 10¹ X 1.25 X 10⁶ = 8.5 X 10⁷ in scientific notation).

Now multiply that number by the dilution factor of the dilution made when the bacteria was mixed with dye.

One ml of bacter was mixed with 1ml of dye. This is a 1/2 dilution. The dilution factor or inverse of 1/2 is 2/1.
85,000,000 X 2 = 170,000,000. (8.5 X 10⁷ X 2 = 1.7 X 10⁸ in scientific notation.)
There are 170,000,000 E. coli per cc in the original sample. (In scientific notation, the answer would be 1.7 X 10⁸.)

6. State the function of a spectrophotometer.

7. State the relationship between absorbance (optical density) and the number of bacteria in a broth sample.

8. State the relationship between percent light transmitted and the number of bacteria in a broth sample.

PROCEDURE

1. Perform a serial dilution of a bacterial sample according to instructions in the lab manual and plate out samples of each dilution using the spin-plate technique.

RESULTS

1. Count the number of colonies on a plate showing between 30 and 300 colonies and, by knowing the dilution of this plate, calculate the number of CFUs per ml in the original sample.

Contributors and Attributions

Dr. Gary Kaiser (COMMUNITY COLLEGE OF BALTIMORE COUNTY, CATONSVILLE CAMPUS)