4.3: Direct Microscopic Method (Total Cell Count)

Last updated
Save as PDF

Page ID: 123040

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

In the direct microscopic count, a counting chamber consisting of a ruled slide and a coverslip is employed.. It is constructed in such a manner that the coverslip, slide, and ruled lines delimit a known volume. It is constructed in such a manner that the coverslip, slide, and ruled lines delimit a known volume. The number of bacteria in a small known volume is directly counted microscopically and the number of bacteria in the larger original sample is determined by extrapolation.

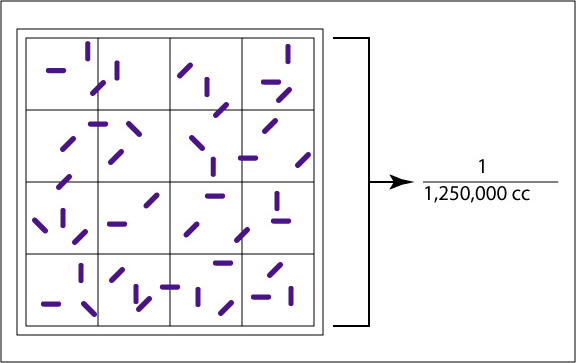
The Petroff-Hausser counting chamber (see Fig. \(\PageIndex{1A}\) and Fig. \(\PageIndex{1B}\) ) for example, has small etched squares 1/20 of a millimeter (mm) by 1/20 of a mm and is 1/50 of a mm deep. The volume of one small square therefore is 1/20,000 of a cubic mm or 1/20,000,000 of a cubic centimeter (cc). There are 16 small squares in the large double-lined squares that are actually counted, making the volume of a large double-lined square 1/1,250,000 cc. The normal procedure is to count the number of bacteria in five large double-lined squares and divide by five to get the average number of bacteria per large square. This number is then multiplied by 1,250,000 since the square holds a volume of 1/1,250,000 cc, to find the total number of organisms per cc in the original sample.

Fig. \(\PageIndex{1A}\) : Large Double-Lined Square of a Petroff-Hausser Counter	Fig. \(\PageIndex{1B}\) : Petroff-Hausser Counter as seen through a Microscope

The large, double-lined square holds a volume of 1/1,250,000 of a cubic centimeter. Using a microscope, the bacteria in the large square are counted.	The double-lined "square" holding 1/1,250,000 cc is shown by the bracket. The arrow shows a bacterium.
(Copyright; Gary E. Kaiser, Ph.D. The Community College of Baltimore County, Catonsville Campus CC-BY-3.0)

If the bacteria are diluted, such as by mixing the bacteria with dye before being placed in the counting chamber, then this dilution must also be considered in the final calculations.

The formula used for the direct microscopic count is:

The number of bacteria per cc =

The average number of bacteria per large double-lined square X

The dilution factor of the large square (1,250,000) X

The dilution factor of any dilutions made prior to placing the sample
in the counting chamber, e.g., mixing the bacteria with dye

Contributors and Attributions

Dr. Gary Kaiser (COMMUNITY COLLEGE OF BALTIMORE COUNTY, CATONSVILLE CAMPUS)