4.2: Plate Count (Viable Count)

Last updated
Save as PDF

Page ID: 123039

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

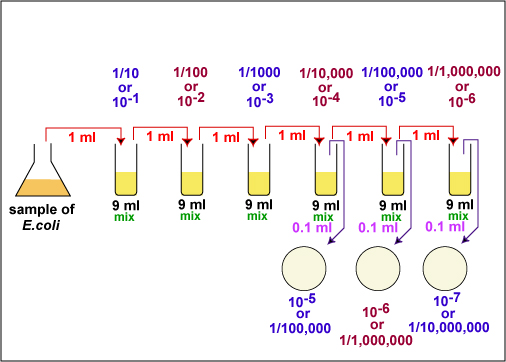
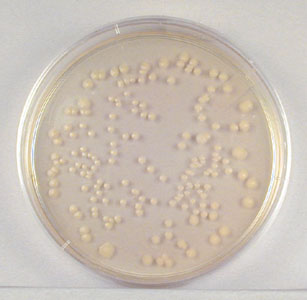
The number of bacteria in a given sample is usually too great to be counted directly. However, if the sample is serially diluted (see Fig. \(\PageIndex{1}\)) and then plated out on an agar surface in such a manner that single isolated bacteria form visible isolated colonies (see Fig. 2), the number of colonies can be used as a measure of the number of viable (living) cells in that known dilution. However, keep in mind that if the organism normally forms multiple cell arrangements, such as chains, the colony-forming unit may consist of a chain of bacteria rather than a single bacterium. In addition, some of the bacteria may be clumped together. Therefore, when doing the plate count technique, we generally say we are determining the number of Colony-Forming Units (CFUs) in that known dilution. By extrapolation, this number can in turn be used to calculate the number of CFUs in the original sample.

Fig. \(\PageIndex{1}\): Plate Count Dilution Procedure	Fig. \(\PageIndex{2}\): Single Isolated Colonies Obtained During the Plate Count

(Copyright; Gary E. Kaiser, Ph.D. The Community College of Baltimore County, Catonsville Campus CC-BY-3.0)

Normally, the bacterial sample is diluted by factors of 10 and plated on agar. After incubation, the number of colonies on a dilution plate showing between 30 and 300 colonies (see Fig. \(\PageIndex{2}\)) is determined. A plate having 30-300 colonies is chosen because this range is considered statistically significant. If there are less than 30 colonies on the plate, small errors in dilution technique or the presence of a few contaminants will have a drastic effect on the final count. Likewise, if there are more than 300 colonies on the plate, there will be poor isolation and colonies will have grown together.

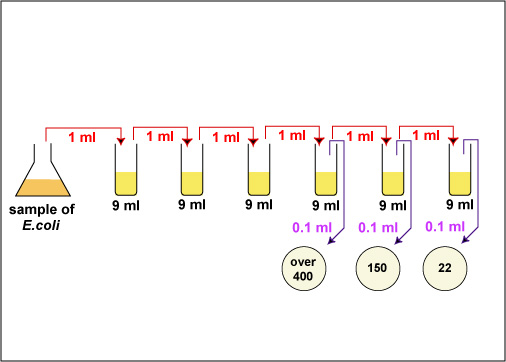
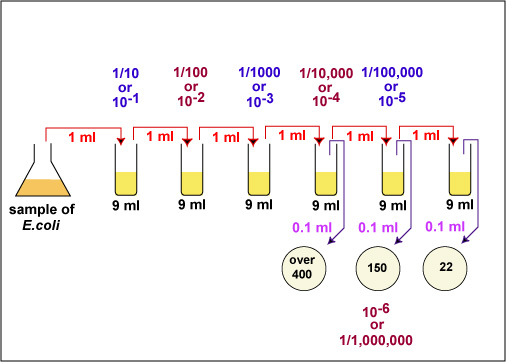
Generally, one wants to determine the number of CFUs per milliliter (ml) of sample. To find this, the number of colonies (on a plate having 30-300 colonies) is multiplied by the number of times the original ml of bacteria was diluted (the dilution factor of the plate counted). For example, if a plate containing a 1/1,000,000 dilution of the original ml of sample shows 150 colonies, then 150 represents 1/1,000,000 the number of CFUs present in the original ml. Therefore the number of CFUs per ml in the original sample is found by multiplying 150 x 1,000,000 as shown in the formula below:

The number of CFUs per ml of sample =

The number of colonies (30-300 plate) X

The dilution factor of the plate counted

In the case of the example above (see Fig. \(\PageIndex{3A}\) and Fig. \(\PageIndex{3B}\)), 150 x 1,000,000 = 150,000,000 CFUs per ml. (1.5 X 10² X 10⁶ = 1.5 X 10⁸ in scientific notation.)

Fig. \(\PageIndex{3A}\): Practice Plate Count Dilution Problem, Step 1	Fig. \(\PageIndex{3B}\): Practice Plate Count Dilution Problem, Step 2

(Copyright; Gary E. Kaiser, Ph.D. The Community College of Baltimore County, Catonsville Campus CC-BY-3.0)

For a more accurate count it is advisable to plate each dilution in duplicate or triplicate and then find an average count.

Contributors and Attributions

Dr. Gary Kaiser (COMMUNITY COLLEGE OF BALTIMORE COUNTY, CATONSVILLE CAMPUS)