6.8: Potential, Kinetic, Free, and Activation Energy - Activation Energy
- Page ID
- 13108
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Discuss the concept of activation energy
Many chemical reactions, and almost all biochemical reactions do not occur spontaneously and must have an initial input of energy (called the activation energy) to get started. Activation energy must be considered when analyzing both endergonic and exergonic reactions. Exergonic reactions have a net release of energy, but they still require a small amount of energy input before they can proceed with their energy-releasing steps. This small amount of energy input necessary for all chemical reactions to occur is called the activation energy (or free energy of activation) and is abbreviated EA.
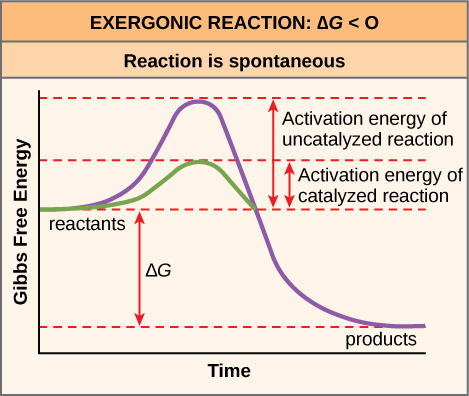
Activation Energy in Chemical Reactions
Why would an energy-releasing, negative ∆G reaction actually require some energy to proceed? The reason lies in the steps that take place during a chemical reaction. During chemical reactions, certain chemical bonds are broken and new ones are formed. For example, when a glucose molecule is broken down, bonds between the carbon atoms of the molecule are broken. Since these are energy-storing bonds, they release energy when broken. However, to get them into a state that allows the bonds to break, the molecule must be somewhat contorted. A small energy input is required to achieve this contorted state, which is called the transition state: it is a high-energy, unstable state. For this reason, reactant molecules don’t last long in their transition state, but very quickly proceed to the next steps of the chemical reaction.
Cells will at times couple an exergonic reaction (ΔG<0) with endergonic reactions (ΔG>0), allowing them to proceed. This spontaneous shift from one reaction to another is called energy coupling. The free energy released from the exergonic reaction is absorbed by the
endergonic reaction. One example of energy coupling using ATP involves a transmembrane ion pump that is extremely important for cellular function.
Free Energy Diagrams
Free energy diagrams illustrate the energy profiles for a given reaction. Whether the reaction is exergonic (ΔG<0) or endergonic (ΔG>0) determines whether the products in the diagram will exist at a lower or higher energy state than the reactants. However, the measure of the activation energy is independent of the reaction’s ΔG. In other words, at a given temperature, the activation energy depends on the nature of the chemical transformation that takes place, but not on the relative energy state of the reactants and products.
Although the image above discusses the concept of activation energy within the context of the exergonic forward reaction, the same principles apply to the reverse reaction, which must be endergonic. Notice that the activation energy for the reverse reaction is larger than for the forward reaction.
Heat Energy
The source of the activation energy needed to push reactions forward is typically heat energy from the surroundings. Heat energy (the total bond energy of reactants or products in a chemical reaction) speeds up the motion of molecules, increasing the frequency and force with which they collide. It also moves atoms and bonds within the molecule slightly, helping them reach their transition state. For this reason, heating up a system will cause chemical reactants within that system to react more frequently. Increasing the pressure on a system has the same effect. Once reactants have absorbed enough heat energy from their surroundings to reach the transition state, the reaction will proceed.
The activation energy of a particular reaction determines the rate at which it will proceed. The higher the activation energy, the slower the chemical reaction will be. The example of iron rusting illustrates an inherently slow reaction. This reaction occurs slowly over time because of its high EA. Additionally, the burning of many fuels, which is strongly exergonic, will take place at a negligible rate unless their activation energy is overcome by sufficient heat from a spark. Once they begin to burn, however, the chemical reactions release enough heat to continue the burning process, supplying the activation energy for surrounding fuel molecules.
Like these reactions outside of cells, the activation energy for most cellular reactions is too high for heat energy to overcome at efficient rates. In other words, in order for important cellular reactions to occur at significant rates (number of reactions per unit time), their activation energies must be lowered; this is referred to as catalysis. This is a very good thing as far as living cells are concerned. Important macromolecules, such as proteins, DNA, and RNA, store considerable energy, and their breakdown is exergonic. If cellular temperatures alone provided enough heat energy for these exergonic reactions to overcome their activation barriers, the essential components of a cell would disintegrate.
The Arrhenius Equation
The Arrhenius equations relates the rate of a chemical reaction to the magnitude of the activation energy:
k=AeEa/RT
where
- k is the reaction rate coefficient or constant
- A is the frequency factor of the reaction. It is determined experimentally.
- R is the Universal Gas constant
- T is the temperature in Kelvin
Key Points
- Reactions require an input of energy to initiate the reaction; this is called the activation energy (EA).
- Activation energy is the amount of energy required to reach the transition state.
- The source of the activation energy needed to push reactions forward is typically heat energy from the surroundings.
- For cellular reactions to occur fast enough over short time scales, their activation energies are lowered by molecules called catalysts.
- Enzymes are catalysts.
Key Terms
- activation energy: The minimum energy required for a reaction to occur.
- catalysis: The increase in the rate of a chemical reaction by lowering its activation energy.
- transition state: An intermediate state during a chemical reaction that has a higher energy than the reactants or the products.
Contributions and Attributions
- OpenStax College, Biology. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...ol11448/latest. License: CC BY: Attribution
- Gibbs free energy. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/Gibbs_free_energy. License: CC BY-SA: Attribution-ShareAlike
- endergonic reaction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/endergonic%20reaction. License: CC BY-SA: Attribution-ShareAlike
- exergonic reaction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/exergonic%20reaction. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...e_06_03_03.jpg. License: CC BY: Attribution
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...05abcd_new.png. License: CC BY: Attribution
- OpenStax College, Biology. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44424/latest...ol11448/latest. License: CC BY: Attribution
- first law of thermodynamics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/first%2...thermodynamics. License: CC BY-SA: Attribution-ShareAlike
- work. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/work. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...e_06_03_03.jpg. License: CC BY: Attribution
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...05abcd_new.png. License: CC BY: Attribution
- System Boundary. Provided by: WikiPedia. Located at: commons.wikimedia.org/wiki/Fi...m_boundary.svg. License: CC BY: Attribution
- File:Soyuz TMA-05M rocket launches from Baikonur 4.jpg. Provided by: File:Soyuz TMA-05M rocket launches from Baikonur 4.jpg. Located at: commons.wikimedia.org/wiki/Fi...Baikonur_4.jpg. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Laws of Thermodynamics. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44424/latest...e_06_02_01.jpg. License: CC BY: Attribution
- OpenStax College, Biology. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44424/latest...ol11448/latest. License: CC BY: Attribution
- second law of thermodynamics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/second%...thermodynamics. License: CC BY-SA: Attribution-ShareAlike
- entropy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/entropy. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...e_06_03_03.jpg. License: CC BY: Attribution
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...05abcd_new.png. License: CC BY: Attribution
- System Boundary. Provided by: WikiPedia. Located at: commons.wikimedia.org/wiki/Fi...m_boundary.svg. License: CC BY: Attribution
- File:Soyuz TMA-05M rocket launches from Baikonur 4.jpg. Provided by: File:Soyuz TMA-05M rocket launches from Baikonur 4.jpg. Located at: commons.wikimedia.org/wiki/Fi...Baikonur_4.jpg. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Laws of Thermodynamics. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44424/latest...e_06_02_01.jpg. License: CC BY: Attribution
- OpenStax College, The Laws of Thermodynamics. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44424/latest...e_06_02_02.jpg. License: CC BY: Attribution
- OpenStax College, Biology. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...ol11448/latest. License: CC BY: Attribution
- catalysis. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/catalysis. License: CC BY-SA: Attribution-ShareAlike
- OpenStax, Biology. September 29, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/contents/185cbf87-c72...f21b5eabd@9.87. License: CC BY: Attribution
- activation energy. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/activation_energy. License: CC BY-SA: Attribution-ShareAlike
- transition state. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/transition_state. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...e_06_03_03.jpg. License: CC BY: Attribution
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...05abcd_new.png. License: CC BY: Attribution
- System Boundary. Provided by: WikiPedia. Located at: commons.wikimedia.org/wiki/File:System_boundary.svg. License: CC BY: Attribution
- File:Soyuz TMA-05M rocket launches from Baikonur 4.jpg. Provided by: File:Soyuz TMA-05M rocket launches from Baikonur 4.jpg. Located at: commons.wikimedia.org/wiki/Fi...Baikonur_4.jpg. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Laws of Thermodynamics. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44424/latest...e_06_02_01.jpg. License: CC BY: Attribution
- OpenStax College, The Laws of Thermodynamics. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44424/latest...e_06_02_02.jpg. License: CC BY: Attribution
- Endothermic Reaction. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/Fi...c_Reaction.png. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Potential, Kinetic, Free, and Activation Energy. October 16, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m44425/latest...e_06_03_04.jpg. License: CC BY: Attribution


