16.8: Lotka-Volterra formulation
- Page ID
- 26231
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Competition equations are usually presented in textbooks as the Lotka–Volterra competition model. This first appeared in the ecological literature in the 1920s and is defined not just in terms of the interactions among species, but also in terms of the species’ carrying capacities, as follows.

Figure \(\PageIndex{1}\). Case 1: Species 2 excludes Species 1. Case 2: Species 1 excludes Species 2. Case 3: one excludes the other, depending on starting conditions. Case 4: both species coexist.
\[\frac{1}{N_1}\frac{dN_1}{dt}\,=\,r_1(1-\frac{N_1+a_{1,2}N_2}{K_1})\]
\[\frac{1}{N_2}\frac{dN_2}{dt}\,=\,r_2(1-\frac{N_2+a_{2,1}N_1}{K_2})\]
\(K_1\) and \(K_2\) are the carrying capacities for Species 1 and 2, respectively. Parameters \(a_{1,2}\) and \(a_{2,1}\) represent the interference by each species on the other. If \(a_{1,2}=2\), for example, each individual of Species 2 interferes with the growth of Species 1 as if it were two individuals of Species 1. If, on the other hand, \(a_{1,2}=1/2\), it takes two individuals of Species 2 to have the same negative effect on the growth of Species 1 as one individual of Species 1 itself.
To compare this with the RSN formulation, represent Equations 16.7.1 and 16.7.2 with \(i\) and \(j\) subscripts
\(\frac{1}{N_i}\frac{dN_i}{dt}\,=\,r_i(1-\frac{N_i+a_{i,j}N_j}{K_i})\)
and multiply the right hand side through by \(r_i\),
\(\frac{1}{N_i}\frac{dN_i}{dt}\,=\,r_i\,-\frac{r_i}{K_i}N_i\,-\frac{a_{i,j}r_i}{K_i}N_j\)
This shows that the Lotka–Volterra formulation is isomorphic to the RSN formulation. All conclusions about competitive systems examined thus far apply to the Lotka–Volterra formulation as well, with the appropriate translation of parameters. Parameter \(r_i\) is the same in both in the Lotka–Volterra formulation and the RSN formulation, but \(s_{i,i}= −r_i/K_i\) and \(s_{i,j}=−a_{i,j}r_i/K_i\).
Beware, however, of a widely quoted statement derived from this formulation that appears throughout the ecological literature and textbooks. Statements like “Coexistence requires that each species inhibit itself more than it inhibits the other species” are abundant in textbooks and in the ecological literature. Alas, those statements are not correct.
box \(\PageIndex{2}\)
Coexistence in the Lotka–Volterra model requires that each species be able to increase from low densities when the other species is at its single-species equilibrium.
To see this, examine Figure 16.21. Here Species 1 inhibits itself with s11 =−1, while it inhibits the other species more strongly with s12 =−1.153. Yet there is global coexistence. Evidently, coexistence does not require that each species inhibit itself more than it inhibits the other, as in the conventional wisdom. The confusion in the literature has apparently emerged from the presence of the carrying capacity terms, K1 and K2, in the Lotka–Volterra formulation. These terms obscure the effects of the interaction terms, a1,2 and a2,1, when carrying capacities differ between the species.
What, then, is a correct statement about coexistence? It can be put in terms of increasing from low densities, as shown in Box \(\PageIndex{2}\). The qualifying phrase “from low densities” is required, because the species not present can increase from high densities in a bistable system, as in Figure16.20, and flip it to the other state, even though coexistence cannot occur.
Another way in which coexistence has been explained is by Vandermeer (1981 Bioscience), connecting coexistence with a certain kind of “overyielding,” wherein two crops require less land for the same annual productivity when growing together than when growing apart.
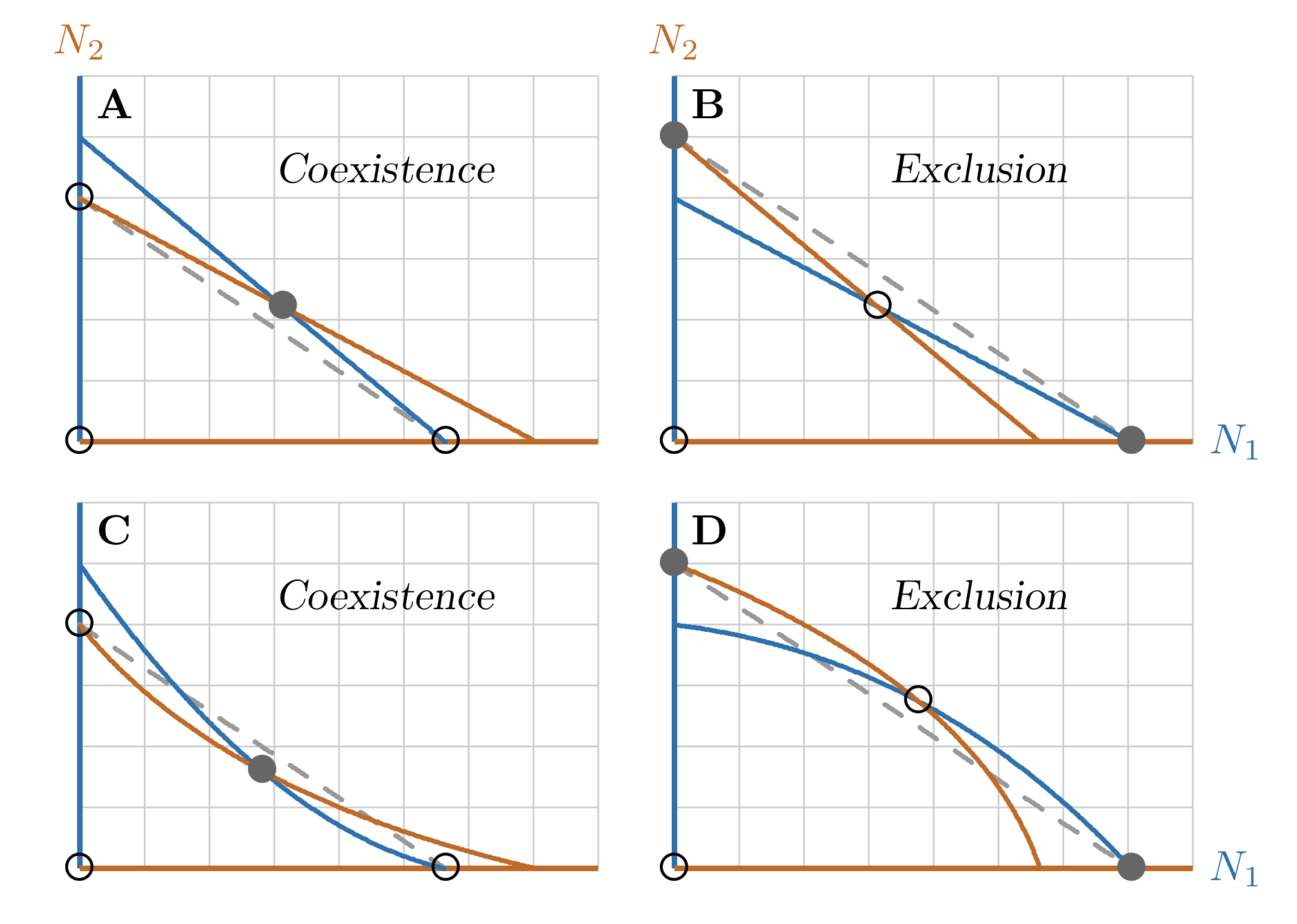
Figure \(\PageIndex{3}\). Coexistence in terms of a kind of overyielding (Vandermeer 1981, Bioscience).
The test is whether the joint equilibrium is above a line connecting the single-species equilibria (dashed gray in Figure \(\PageIndex{3}\)A ) or below the line (Figure \(\PageIndex{3}\)B).
This view is correct for models we have been considering with straight-line isoclines, but incorrect for more general models with curved isoclines (Figure \(\PageIndex{3}\)C,D ). The statement in Box \(\PageIndex{2}\), however, holds true in each of these cases.
All things considered, rather than relying on rules of thumb, it can be better to evaluate a system directly, for example with the methods of eigenvectors and eigenvalues described in Chapter 10.


