4.2: Membrane Permeability
- Page ID
- 16107
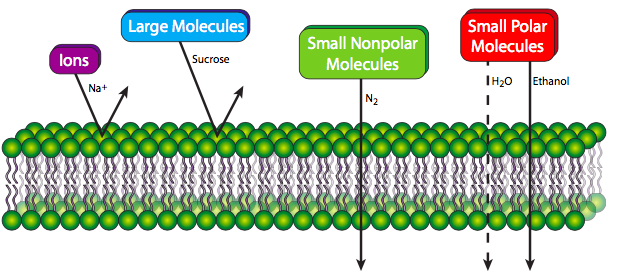
A pure phospholipid bilayer, whatever the lipid composition, is a semi-permeable membrane that is generally repellent to large molecules and to ions. Small polar molecules can sometimes pass easily (e.g. ethanol), but more often pass at low rates if at all (e.g. water). However, small nonpolar molecules are able to pass through the membrane with relative ease. The reasons should be self-evident: larger molecules simply cannot fit between the lipid molecules to make their way through. Small molecules that can fit must be hydrophobic, otherwise the fatty acyl core of the membrane will repel them and block them from proceeding. Higher concentrations of cholesterol, by filling in gaps between phospholipid tails, decreases permeability even for small molecules that can normally pass through the membrane easily. Cells need far more than small nonpolar molecules for their material and energy requirements. Fortunately for life on Earth, the membranes of living cells are not purely phospholipids, and as we will see, proteins embedded in the phospholipid bilayer can form conveyances for the transport of many different molecules in and out of the membrane.
In fact, the observation of saturation kinetics in glucose transport in erythrocyte membranes was the first indication of protein-mediated transport (the GLUT1 glucose transporter). Another telling observation was the finding that glucose permeability through erythrocyte membranes is a million times greater than that through an artificial lipid bilayer. The concentration of glucose in the blood is relatively high compared to that inside of most cells, so this is mediated transport, but passive transport since it is going down the concentration gradient. To facilitate the process by preventing a buildup of glucose concentration in the cell, the first step of glucose metabolism is phosphorylation to convert it into a different molecule, glucose-6-phosphate. Thus the concentration of glucose stays very low, and it flows readily from the bloodstream into the cell.
There are some obvious differences between transport of molecules directly through the lipid bilayer (nonmediated transport) and transport using a protein facilitator embedded in the membrane (mediated transport). Nonmediated transport is governed by diffusion: the solute moves from areas of high concentration to areas of low concentration, thereby eliminating the gradient. As long as a solute (A) can get through the membrane, its flux (J) is determined solely by concentration difference and the permeability (P) of the membrane: JA = PA ([A]out - [A]in) and the relationship between the ux across the membrane and the concentration differential is linear.
This is not the case in mediated transport. As the name implies, a protein intermediary is required, and alarm bells should be going off in your head saying, “there’s a limit,” to the number of available transport proteins at any given time. Therefore, just as we saw with enzyme kinetics in chapter 3, the ux of solutes going through a transporter is not linearly related to the concentration differential across the membrane, though there is still a concentration effect. Instead, the relationship is logarithmic, reaching a saturation plateau once all the available transport proteins are in use. At that point, increasing the concentration of the solute will not increase its flux across the membrane. Thus for simple unidirectional mediated transport of a solute (\(B\)), the flux (\(J\)) can be expressed as a value of the affinity of the transporter for the solute (\(K_M\)) and the concentration of the solute:
\[J_B = \dfrac{J_{max}[B]}{K_M + [B]}\]
Membrane permeability allows for the possibility of concentration gradients across membranes, which in turn have potential energy associated with the concentration dif- ferential across the membrane. This turns out to be a phenomenally important source of cellular energy, and is the basis for aerobic synthesis of ATP by oxidative phosphorylation (chapter 5). However, to have a meaningful discussion of how concentration differences across semipermeable membranes store energy, we should review some basic concepts rst.
If a point source (e.g. a “glob”) of a solute (e.g. honey) is placed into a solvent (e.g. tea), it starts to dissolve, and as it does so, the concentration of solute near the point source will start out much higher than the concentration towards the periphery of the container (e.g. teacup). Over time, the solute then diffuses from the point source outward in all avail- able directions, and eventually the concentration of solute is equal at any point in tea- cup-space. This behavior is governed by the Second Law of Thermodynamics. The solute is initially concentrated, which means that its constituent molecules are relatively orga- nized. By the second law, these molecules will tend toward chaos, moving away from the constraints of the initial point toward an area with lower concentrations of the solute.
Now, imagine a temporary wall around the point source. The natural tendency is for the solutes to spread out, so by preventing that movement, you have bottled up some potential energy. Of course, this is only potential energy if there is some chance that the solutes can eventually go through the barrier (e.g. the wall has windows that can be opened). If the solutes have absolutely zero chance of passing through, then there is no potential energy because there is no potential to get out and about. Recalling the Energy chapter in which the second law was introduced, the chemical potential energy of a solute is
\[G=RT \ln[A]+G^\prime\]
so the chemical potential difference across a membrane is then
\[ΔG= RT \ln \left(\dfrac{[A_i]}{[A_o]}\right).\]
Now imagine this as something like a hydroelectric dam, where there is a great deal of pressure building up behind the dam, which can be utilized when some of the water is allowed through, powering turbines that generate electricity. In the biological case, there is concentration pressure building up both inside and outside the cell because the natural thermodynamic tendency is to bring the inside and outside concentrations of each solute to equilibrium. When this pressure is released by allowing the ions or other molecules to ow across the membrane, energy is released, and may be captured and used. The most direct example of this the proton-gradient-driven ATP synthase in the inner mitochondrial membrane (Chapter 5), which contains a direct molecular equivalent to the turning of a water wheel with the ow of water. For another example, if we look at [Na+] in an animal cell, the extracellular concentration is much higher than that intracellularly. When a Na+ channel is opened, the Na+ ions rush inward to try to equalize the concentration of Na+ inside and outside of the cell. Equilibrium is not actually reached in a living cell because Na+ channels are tightly regulated and only open for short periods of time.
In cells, concentration gradients of ions are great energy sources because the lipid part of the membrane is strongly repellent to ions, preventing them from passing through, but the membrane is embedded with channels and transporters that can allow the ions through if and when they are open. Because ions have both concentration differentials and charge differentials across the membrane, the electrochemical potential difference across the membrane is represented by a modification of the chemical potential difference equation with a term that takes that electrical charge into account:
\[ΔG=RT \ln \left( \dfrac{[A_i]}{[A_o]}\right) + ZFΔΨ\]
Z is the charge of the ion (e.g. +1 for Na+, -1 for Cl-, +2 for Ca2+), F is the Faraday constant (9.6485 x 105 C/mol), and ΔΨ is the membrane potential. In an average animal cell, the membrane potential is approximately -70mV. The number is negative to show that the inside of the cell is negative with respect to the outside. Thus, again considering Na+, not only is there a chemical gradient of more Na+ ions outside the cell than inside, there is also a charge gradient of more positive charges outside the cell to inside, so both forces contribute to the energy of Na+ flow into the cell. The equilibrium potential of one ion (e.g. Na+) across a membrane is determined by the Nernst equation:
\[E_m= \left(\dfrac{RT}{zF}\right) \ln \left(\dfrac{[Na^+]_{out}}{[Na^{+}]_{in}}\right)\]
which is extended in the Goldman equation (also Goldman-Hodgkin-Katz equation) that calculates membrane potential based on multiple ion gradients. For most ani- mal cells, a good approximation of the overall membrane potential can be calculated using the three major gradients: Na+, K+, and Cl-. There are, of course, other ion gradients, but their contributions are normally much smaller than these three.
The membrane potential is relatively stable in non-excitable cells, but in neurons and muscle cells, the membrane potential is quite dynamic, so the membrane potential in a non-excited state is referred to in these cells as the resting potential. The membrane (resting) potential in most animal cells is around -70mV. This is due in large part to the presence of K+ leak channels. These channels leak K+ from the cell down the concentration gradient until the chemical potential difference of K+ is at equilibrium with the membrane potential. In other words, the gradient pushing K+ out will eventually be stopped by an equal force from the gradient pushing positive ions (including K+) back in. There are also Na+ and Cl- leak channels, but there are far fewer and they contribute far less to the resting potential than K+.
Potassium leak channels are structurally as well as functionally different from other potassium channels. Where most K+ channels have one pore domain, the leak channels have two. While leak channels, by definition are not voltage gated, nor appreciably activated or inactivated, this is not true of all members of the tandem pore domain family of potassium channels. Interestingly, some (e.g. TASK-1) are mechanoreceptors, opening in response to membrane stretch, and others act as thermoreceoptors, with heat-sensitive activation (e.g. TREK-1).
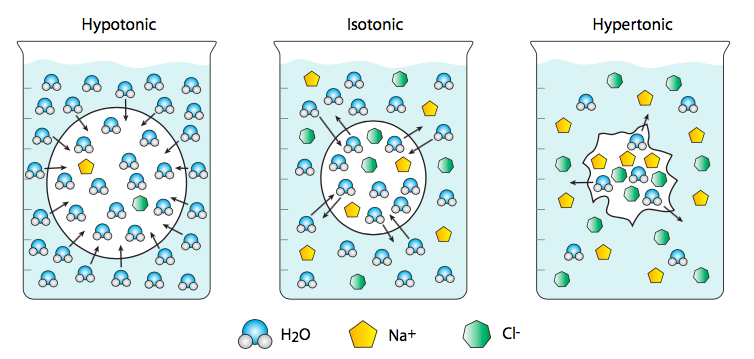
Although we most commonly think of water as the solvent in which “interesting” molecules (e.g. ions) diffuse, its concentration and movement across membranes has important biological consequences. Osmosis is a term that specifically refers to the diffusion of water across a membrane. In this case, water is considered a solute rather than a solvent, so that if a water-permeant liposome, embedded with aquaporin channels to allow the passage of water, is placed in a very salty saline solution, the cell will shrink because there is a lower ratio of water to dissolved salts outside of the cell than inside. This is a hypertonic solution relative to the cell. Therefore the water flows from the cell (higher water concentration) out into the saline (with lower water concentration). Conversely, a cell placed in distilled and deionized water will swell and potentially burst because the water rushes from the highest possible concentration (pure water) to a cytoplasm with lower water concentration (because dissolved in it are various ions and other molecules). This is an example of a hypotonic solution. An isotonic solution will have the same concentration of water inside and outside of the cell.