10.1: Cladistics

The more contemporary, much more formalized than expert-based is cladistics. Below, cladistic procedure is explained using artificial example of three organisms. The goal of the analysis is the creation of a phylogeny tree (cladogram) which becomes the basis of classification. Below is a short instruction which explains the basics of the cladistic analysis on the artificial example of several “families” of plants.

1. Start with determining the “players”—all subtaxa from bigger group. In our case, it will be these three “families”:

Alphaceae

Betaceae

Gammaceae

2. Describe these three groups:

Alphaceae: Flowers red, petioles short, leaves whole, spines absent

Betaceae: Flowers red, petioles long, leaves whole, spines absent

Gammaceae: Flowers green, petioles short, leaves dissected, spines present

3. Determine individual characters (we will need at least \(2N+1\) characters where \(N\) is number of studied taxa):

(1) Flower color

(2) Petiole size

(3) Dissection of leaves

(4) Presence of spines

4. Polarize the characters: every character should have at least two character states where “0” is ancestral, plesiomorphic state, and “1” is derived, apomorphic state. To decide which state is plesiomorphic and which is apomorphic, use these kinds of arguments:

(a) Historical evidence (e.g., from fossils)

(b) Developmental evidence

(c) Comparative evidence

5. If this information is absent, find the outgroup which is the most ancestral, most early divergent taxon related to our groups. In our case, we will employ outgroup:

Omegaceae: Flowers green, petioles short, leaves whole, spines absent.

6. Label characters with “1” (apomorphic) or “0” (plesiomorphic):

(1) Flower color green—0; red—1

(2) Petiole size small—0; big—1

(3) Dissection of leaves absent—0; present—1

(4) Absence of spines—0; spines present—1

7. Make character table containing both subtaxa and labeled characters:

	(1)	(2)	(3)	(4)
Alphaceae	1	0	0	0
Betaceae	1	1	0	0
Gammaceae	0	0	1	1

(Outgroup, Omegaceae evidently has all zeroes.)

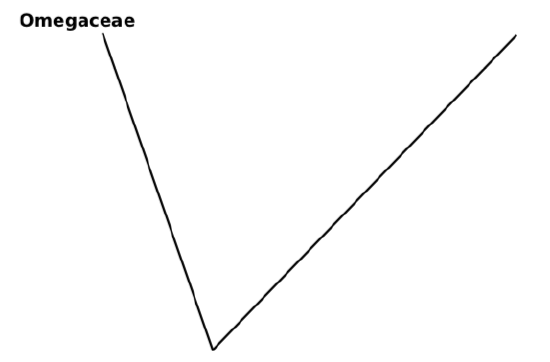
8. Start the tree from outgroup (this step is not absolutely necessary but will make phylogeny more clear):

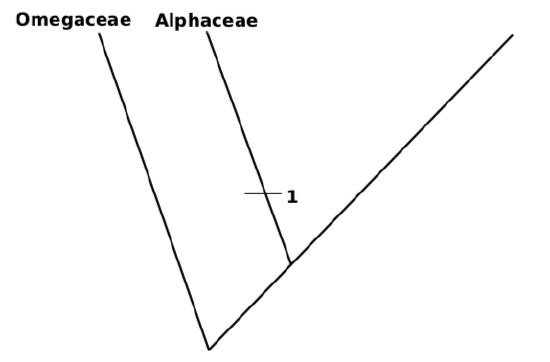
9. Most ancient ingroup (Alphaceae) is a first branch, label it with bar which shows acquisition of the advanced state of first character (red flower color):

10. Attach more and more sub-taxa. It is possible to do this randomly (like most of phylogeny software), or attach groups to make shortest tree. For example, Betaceae and Gammaceae have equal number of synapomorphies but Betaceae have only one character different from Alphaceae it is sensible to attach it first, and then attach Gammaceae:

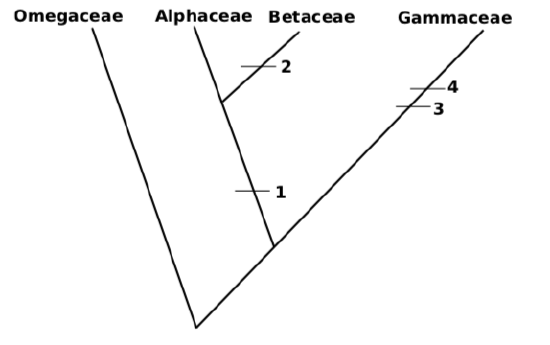
This tree has 4 evolutionary events (length \(=4\))

11. If Gammaceae was attached first, then resulted tree will be be one step longer:

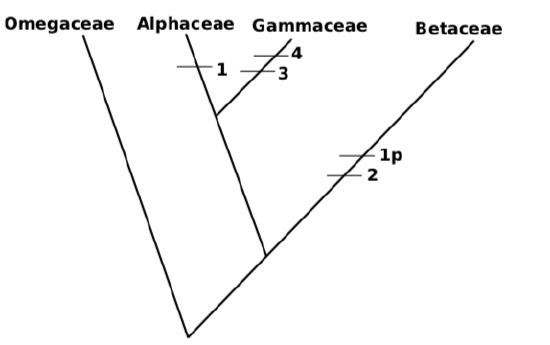
There are five evolutionary events; in other words, length of tree \(=5\). (“p” are parallel characters (homoplasies); there might be also reversals (“r”), when apomorphic character disappears).

There could be also tree with length \(=6\), or even more if tree includes character reversals, but all of them will be longer than the first one.

12. Choose the shortest, most parsimonous tree. Second tree has 5 events, first tree has 4 events, others could be only longer. Consequently, we choose the first tree. By the way, many computer programs do not follow the procedure above strictly and simply produce all possible trees, and finally choose the shortest.

13. Use the chosen tree as a source of classification:

Order Alphales

1. Family Alphaceae

2. Family Betaceae

Order Gammales

1. Family Gammaceae

This step is needed only if you wish to convert cladogram into traditional, classification. In fact, cladograms are rank-free and might be used as is.

Cladograms often used as source of time trees which are made with genetic information and information from fossils. If we know the age of taxonomic group, we can use it as more objective replacement of rank.

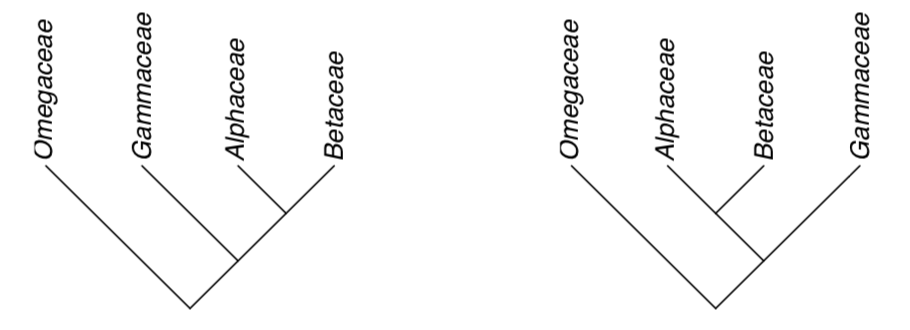
Ability to review and compare phylogenetic trees requires understanding of several basic rules, for example:

1. Tree edges may be freely rotated in any direction. For example, these trees are same:

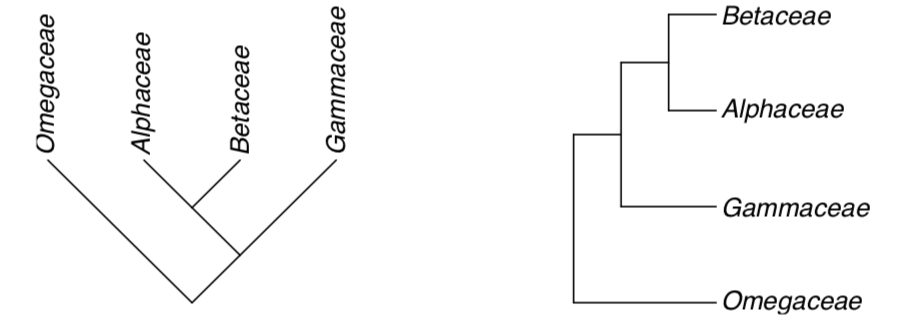
2. Direction of branches also does not matter. These trees are same:

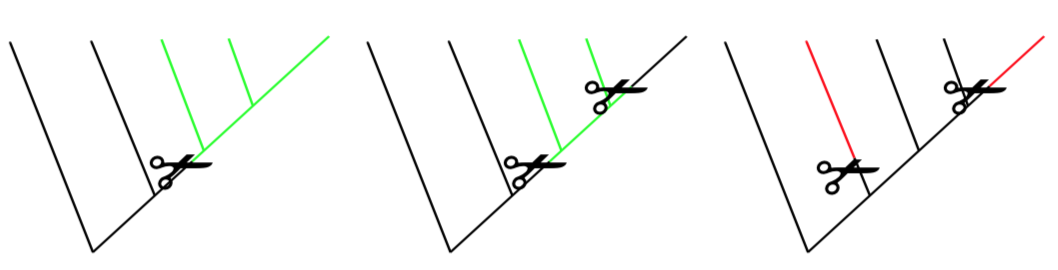
It is not always simple to make classification from a tree. On the previous example, we simply designate the whole branch as a taxon (order which contains our three families). There are situations when only middle part of the branch seems to be acceptable as a taxon. In these cases, remaining part is called paraphyletic taxon.

Paraphyletic groups include all immediate ancestors of its members but not all descendants of these ancestors. Good example of paraphyletic taxon are reptiles: when we take mammals and birds from amniote branch, reptiles will be what is left. Gymnosperms (all seed plants without angiosperms) is another example, but in this case some molecular trees show that gymnosperms is also a natural branch (i.e., monophyletic group). Monophyletic groups include all immediate ancestors and all their descendants.

When the group contains taxa from different branches, it is polyphyletic. Polyphyletic groups are not allowed.

Figure \(\PageIndex{1}\): Monophyletic, paraphyletic and polyphyletic groups, respectively.

Another important distinction between groups of the phylogeny tree is stem and crown groups. All extant members together with their immediate ancestors form a crown of taxon (Figure \(\PageIndex{2}\)). If one member of crown went extinct, we can estimate that it was somehow similar to other crown members. In other words, if we find a way ho to re-create mammoth, we probably understand how to feed it because it belongs to the Elephantidae family crown. However, if the fossil, extinct members of taxon branch outside of crown (stem groups), there are much less taxonomic estimations. It is hard to guess, for example, how to care for Archaeopteryx “dinosaur bird” because such organisms are not exist now and have no living similarities.

Figure \(\PageIndex{2}\): Crown (green skull) and stem (red skull) extinct groups among extant groups.