1.25: Plant growth—patterns, limitations and models
- Page ID
- 70344
One of the marvels of life is growth, the ability of organisms to get bigger. This is especially the case for plants since they grow literally and figuratively 'out of thin air.' And while plant growth is a very ordinary phenomenon, its explanation is very much 'extra-ordinary, ' as they are able to accumulate scattered pieces of their environment and assemble them into an organic entity. In contrast, animals need only to find pre-assembled pieces of life, perhaps still living, perhaps not, and reconfigure them to their own use. And while the controls on animal growth are straightforward, being tied to ingestion, what controls plant growth is less obvious.
When plants grow, they generally get bigger both in size and in weight and the process of growth can be linked to increases in either. However, for a variety of reasons, the growth of plants is defined as an irreversible increase in size, not an increase in weight. Part of the reason for this is because water absorption and loss can change plant (wet) weight substantially because of processes that most would not consider growth. For example, trees gain a considerable amount of water overnight to replenish that lost during the day; most would not consider the overnight weight gain to begrowth northe loss during the day tobe 'negative growth.' To avoid the dynamics of water, one might monitor growth with increases in 'dry weight' , a consequence of the accumulation of carbon, nitrogen, phosphorus, etc., and the synthesis of organic molecules such as carbohydrates and proteins. But defining growth by an increase in dry weight would lead to some counterintuitive results. Most would consider that trees grow in the spring when the shoots elongate and leaves appear. At this time the tree is actually decreasing in dry weight. During the summerin temperate areas, as trees photosynthesize and absorb nutrients, their dry weight increases, yet manyare not getting bigger in terms of longer shoots. Similarly, a sprouting seed, which most would consider to be growing, is actually decreasing in dry weight until its photosynthetic rate exceeds its respiration rate; thisgenerally doesn't happen until the seedling is a couple of weeks old and already of substantial size. Consequently, plant growth is typically defined as an irreversible increase in size.
TOPICS
- Growth processes
- Limitations on plant growth
- Growth models
Growth Processes
Increases in the size of plants come about as individual cells, produced by cell divisions in the meristems, expand. While this may seem at first a simple phenomenon , consider the following aspects of the process:
- A ll plant cells, even small ones, are surrounded by a confining cell wall, whose most basic function is to prevent expansion. This allows the cell to pressurize and this is important to plant cell water balance and functioning.
- As the cell expands the thickness of the cell membrane and the cell wall outside it do not diminish. In contrast, consider an expanding balloon: as you blow air into it, the 'skin' of the balloon is stretched thinner and thinner as the static volume of balloon material is spread over a larger and larger volume. This does not happen as plant cells grow–consequently, the expansion must be coordinated with the production of new material for the cell membrane and cell wall; this keeps the thickness of the boundaries of the cell constant. The significance of this, especially with respect to the membrane, should be apparent; stretching the plasma membrane is not possible, only the tearing of it, and this would destroy its ability to be a selective barrier, keeping some molecules in and others out of the cell.
- Although the expansion of the cell is a consequence of water absorption, this is not a simple 'dilution' of the cell. Similar to what is happening in the membrane and wall, the cell is adding intracellular components at a rate that keeps pace with its expansion.
- Although the cytosol does increase its volume as a cell grows, it is generally the expansion of the vacuole that accounts for most of the increased volume of the cell. Assuming that a larger cell is beneficial to the organism (because it allows it to penetrate more of its environment, important for both roots and shoots), the large central vacuole is a relatively 'cheap' way for a cell to get bigger because the contents of vacuole take less energy to obtain than the contents of the cytosol. T he enlarged cell is not simply a diluted and stretched version of the original one, it s walls and membranes are the same thickness as before and the cytosol is the same composition as before. The cytosol has increased somewhat in volume but the majority of the increase in overall cell volume is the result of a larger vacuole, which must have the same solute concentration as the cytosol, but the solutes are different and 'cheaper' ones are in the vacuole.
- The region of growth of a plant is separated, often by very substantial distances, from the source of materials for that growth. What materials are needed for growth? We can identify three basic needs: water, which represents the biggest component of 'new plant' material; carbohydrates which are used both in cellular respiration, to provide energy for synthetic reactions, and also as building materials to make cell walls, cell membranes, internal membranes, proteins, metabolites, vitamins, etc; and mineral nutrients, phosphorus for membranes, nitrogen for amino acids, etc. Water and nutrients are coming from the soil and are thus very close to the growing cells of root meristems, but must be transported considerable distances to get to the tips of shoots, up to 350 feet in the case of a redwood tree. Carbohydrates are supplied by photosynthesizing leaves, which may be relatively close to growing shoots but may be 350 feet away from an expanding root meristem. Carbohydrates often do not directly flow from leaves to growth points but instead may flow from leaves to storage sites and then from storage sites to growth regions.
Cellular expansion is resisted by the strength of the cell wall and expansion occurs when the pressure inside the cell, created by the inward diffusion of water, exceeds the strength of the wall. Growing cells have 'softer' cell walls, i.e., walls that yield (expand) at lower pressures than non-growing cells. And it is believed that plants control cellular growth by controlling the 'softening' of cell walls. To summarize, plant growth involves a coordinated process of the synthesis of membranes (both the cell membrane and the vacuolar membrane), (2) cell wall, (3) cytoplasmic materials (proteins, membranes, metabolites), and (4) vacuolar materials, along with the absorption of water. The size of a cell is determined by genetics and environmental conditions. Growth stops when the wall 'hardens' and no longer yields to the pressure generated by water diffusion. In those cells that have secondary cell walls additional cell wall material is deposited after cell expansion has ceased—note that while secondary wall materials are added the cell is not growing in size but is growing in mass.
As described above the growth of plants is a result of the expansion of cells, not of cell division, which, as the name implies, simply partitions existing structures and does not produce anything that is bigger in size. However, cell division is essential to the growth process because it provides cells that have the potential to grow, i.e., cells that accumulate solutes and produce cell walls that will yield to the pressures that develop inside them. Cell division occurs in plants in isolated spots called meristems and the actual growth of plants generally occurs in areas adjacent to these meristems. The expansion of newly produced cells pushes the meristematic regions further away from the main body of the plant, expanding the total size of the plant. Thus there is a spatial separation between the region of cell division and the region of cell growth. Action generally occurs simultaneously in both regions. Growth occurs whenever the new cells produced by the meristem are allowed to expand. For some plants, growth is more or less continuous and steady as long as environmental conditions (in particular temperature, water and light) are steady. However, most plants exhibit episodic growth with bursts of cell production and expansion followed by periods of inactivity, even when conditions are constant and favorable. For many perennial plants living in areas with seasonal climates, growth is strictly seasonal, occurring for only a portion of the year. Often the growth period is only a very small portion of the 'favorable' time period. For example, most trees in this area grow only for two to four weeks in May.
The patterns described above represent the extensional growth exhibited by apical meristems in roots and shoots (primary growth) and the expansional growth produced by the lateral meristems (secondary growth). The growth of leaves and fruits is slightly different; these determinate organs have a pattern similar to that of many animals where there is a period of cell division followed by a period of cell expansion. Often, there may be a period of overlap where both division and expansion are occurring but at some point, cells stop dividing and no more embryonic cells are produced. Growth is sustained as the new cells expand but eventually, the growth of the organ stops, and a structure of unchanging size remains yet it does continue to develop.
In order to sustain growth, a supply of materials is needed, not just the water that powers cellular expansion, but the materials to make more cell walls, cell membranes and all the cytoplasmic constituents as the cell expands. Not only are materials needed to construct the enlarging cells, material is also needed to supply the energy that is needed for these processes. Every peptide bond requires the hydrolysis of an ATP, as does every additional glucose unit in a growing cellulose polymer. In addition to direct 'construction costs' energy is needed for other cellular processes, e.g., the transport of molecules across membranes.
Limitations on growth
Many people are interested in making plants grow more, producing more material in a shorter period of time. What is it that limits growth? Below are listed some significant factors, several of which operate in multiple ways. Although increases in all of these factors mayincrease growth, this response is not constant and often tapers off with further increases in the factor, leading to the phenomenon of saturation, where further increases in the factor cause negligible changes in growth. Moreover, for all of these factors, there can be 'too much of a good thing' and further increases actually diminish growth (toxicity).
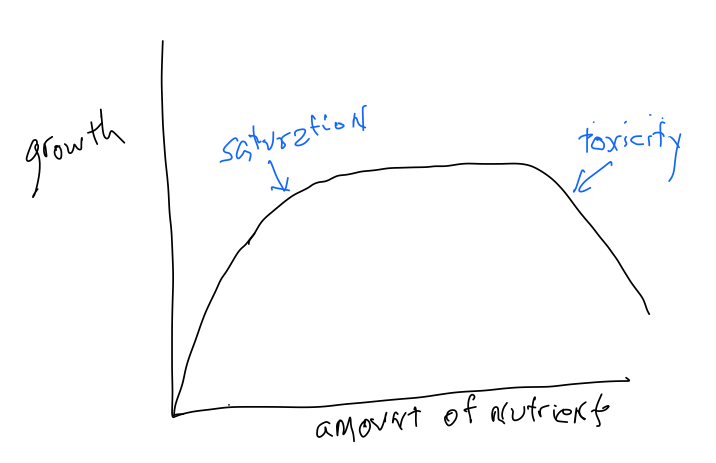
Nutrients
All of the required mineral elements can potentially limit growth. The limitation can come about both because that element is lacking from the soil or because, although the element is present, it is unavailable because of soil conditions. For instance, iron is frequently unavailable in basic soils even though it may be present in abundance. The problem is that under aerobic, basic conditions very little iron is present in a form that readily dissolves.
Somewhere on earth, there are soils that are deficient in all of the 14 mineral elements required by plantsand deficiencies can develop even for elements like molybdenum that are needed in very small amounts. In the early 19th century Carl Sprengel developed an idea later championed by Justus van Liebig called the 'Law of the Minimum:' that plant growth will be limited not by nutrient availability generally but by whatever nutrient is in the shortest supply relative to how much is needed. For example, although additions of nitrogen often increase plant growth, if there isn 't enough molybdenumavailablesuch additions will not result in any growth enhancements. One can think of growing crops to be like baking a cake: if the cake recipe calls for five ingredients, making a cake can be limited by any of the five ingredients, and a lack of one is not made up for by excesses in others. This is a very straightforward idea that applies in many situations. But it runs counter to the common idea that response to factors will always be the constant:' if a little bit is good then a lot must be better'is generally notthe case!
While too little of the essential nutrients can limit growth, too many of the same elements (toxicities) can also retard growth. The most common toxicities are the result of saline soils that have high levels of K, Ca, Cl, SO 4 and Na but unique soil conditions (waterlogging) can also bring about toxicities in iron and manganese in non-saline soils.
Water
Water is probably the most important factor limiting terrestrial photosynthesis worldwide. Water plays multiple roles in plant growth: as a reagent in photosynthesis, as the main constituent of any new cell that is produced, as the transport medium which moves materials throughout the plant and in particular to the growing regions. While all of the above might potentially play a role, the effect of water comes primarily because of the interplay between water loss and carbon dioxide gain. In dry habitats, plants keep their stomates closed to avoid water loss. This lowers the carbon dioxide concentrations inside the leaf and lessens the amount of photosynthesis. Additionally, plants may reduce water loss by having smaller leaves or fewer leaves, both of which may limit growth because the total amount of leaf area determines the amount of photosynthesis that can occur. While lack of water can reduce growth, t oo much water is also damaging to most plants, primarily because waterlogged soils become anaerobic and the roots grow poorly and/or die.
Light
Without light, photosynthesis can't occur and without photosynthesis, growth cannot occur. Light can have a very significant effect on photosynthesis and growth but only when other conditions are favorable to sustain growth and only when dealing with light levels comparable to those typically experienced by the plant. Too much light can be extremely harmful for a number of reasons and plants adapted to the shade usually do very poorly if exposed to high light levels. For the home gardener, the proper location of ornamental plants is strongly influenced by light considerations. The amount of light a plant receivesis controlled both by the intensity of light and by the duration of light exposureand the effects do not always compensate for each other, i.e., short periods of very bright light are not equivalent to longer periods of less bright light. Most crop species are adapted to high light conditions and will do very poorly if grown under shaded conditionsand it is probably the casecrop growth can bereduced as a resultof prolonged cloudy conditions. However, such conditions are often associated with frequent rains and these might also be the cause of decreased growth if the soils become flooded.
Leaf distribution and longevity are important plant parameters that are influenced by light considerations because of problems associated with self-shading. In general, leaves are produced in ways that lessen self-shading and allow for more photosynthesis. Older leaves, that are experiencing shaded conditions, are often abandoned (i.e., they senesce and abscise) because they no longer obtain enough light to be profitable in an energetic/material sense. This is reflected in the following equation:
Net photosynthesis = gross photosynthesis – respiration
Assuming that the maintenance cost (i.e., that the amount of respiration needed for a leaf to maintain its living condition)of a leaf is constant, shading will decrease gross photosynthesis to the point that net photosynthesis is negative, i.e., the leaf costs more to maintain than it 'makes' in photosynthesis. At this point it the plant can cut its losses by eliminating the leaf.
Temperature
Plants are poikilothermic, their temperature is not regulated internally but is determined by the environmental conditions. Moreover, plants have a range of temperatures within which they can survive (often this range of tolerance shifts seasonally). All biological processes, and in particular photosynthesis, respiration, and growth , are influenced by temperature (chapter 26) and, with a few important exceptions, the basic response is that that plant activities, including growth, increase at higher temperatures in the range of 0 to 20 C (32 to 68 F). However, all plants have a n optimum temperature for growth, above which growth diminishes with increasing temperature. Part of the explanation of this is that at higher temperatures respiration is more sensitive to temperature (i.e., increases more with increases in temperature) than photosynthesis–thus although gross photosynthesis might increase, respiration increases more and there is a decrease in net photosynthesis at higher temperature (see equation above).
Interactions between water, light and temperature
These factors are often intertwined: more light increases temperature and higher temperatures increase transpiration and can lead to complications from a lack of water. How tightly these three factors are linked depends upon a variety of factors.
Leaf area
As would be expected, plants with more leaves generally grow faster than plants with fewer leaves. This is discussed in the following section.
Models of Plant Growth
What limits plant growth is a critical question, one that has a multitude of practical implications. Clearly, plant growth can be limited by adverse environmental conditions, e.g., lack o f rainfall. But if conditions are ideal for growth, what limits it? Like all organisms, plants grow by acquiring material and incorporating it into their own structure. One might assume that the ability of a plant to acquire material is directly related to its size, with bigger organisms able to acquire more than little organisms. This would result in a positive feedback process of growth: acquisition of resources—>growth—> bigger plant—>greater acquisition of resources—> more growth—> even bigger plant, etc., etc. This idea can be modeled in a set of equations that are predicated on the idea that the growth rate is a linear function of plant size : more plant, more growth ; more growth more plant.
In words, this idea can be expressed in two ways:
- growth rate is determined by plant size
- the growth rate, expressed per unit of plant, is a constant
In mathematical terms these two statements are:
- growth rate = ∆S/∆t = k * S, where ∆S/∆t is the growth rate, the change in size divided by the change in time, S is the total plant size and k is a constant
- (∆S/∆t) * (1/S) = k,
For most biology students this should be familiar because: (1) it sounds like 'exponential' population growth, or perhaps 'geometric' population growth, (2) it is starting to sound like calculus, a course that is often required for biology majors (and perhaps you now see why!)
Calculus can lead to the following, putting these in differential form:
\[\dfrac{dS}{dt} = k S \tag{1a}\]
\[\dfrac{dS}{dt} (1/S) = k \tag{2a}\]
The size (\(S\)) at any time (\(t\)) is given by \[S(t) = S_o e^{k*t} \tag{3} \label{3}\]
Note that while the jump to Equation \ref{3} requires calculus, the idea s of equation 1 and 1a , and their rearrangement in 2 and 2a , should make sense without it. Equation (3) follows from either of the first two.
Thus, one might expect plant growth to be exponential, just as you might expect population growth to be exponential. Note that the meaning of the word 'exponential' has a mathematical meaning that is not equivalent to the one in general use. Exponential growth is not necessarily 'fast' , and indeed, fast is a subjective adjective. In a mathematical sense, exponential is described in equations 1-3, although only 3 has an exponent in it. One could develop similar equations based on leaf area (i.e., that the growth rate per unit leaf area is a constant), with the argument that leaf area, by controlling photosynthesis, dictates growth rates. However, a similar argument could also be made about roots since without water and nutrients photosynthesis isn 't possible. It is easiest to just assume that roots, leaves and everything else are all needed and let S simply be' total plant size'and work with the assumption that plants can acquire more materials at a rate that is a linear function of their size (i.e., equation 1).
But the growth of plants, and the growth of populations, usually is not exponential, at least not for long. Why isn't plant growth exponential? A basic answer is that growth is not controlled by the rate of material acquisition. It is an internally regulated process and it is too simplistic to assume that the rate of growth is a simple function of the ability of leaves and roots to acquire the materials necessary for growth. The internal controls of the plant, including both hormonal controls and molecular controls (e.g., which genes are activated) regulate the processes of cell division and cell expansion and thereby the growth process. In a fundamental sense, this is no different than what was discussed earlier concerning the development of unicellular organisms (see reading on organism development). A second factor involves meristems or more generally regions of growth. If an organism only has a limited region where growth originates and this region has a finite capacity to produce growth, then growth will not be exponential. In the case of a filamentous algae, that grows from a single apical cell, it is easy to see why growth might not be exponential. Similarly, an unbranched stem with a single apical meristem might not be expected to show exponential growth although one with branches, and with branches that can produce more branches, might be expected to.
An economic model of plant growth
A useful analogy for plant growth is an economic, 'business' model. Gross income is first split between expenses (the costs of running the business) and net income ( 'earnings' , what is left behind after expenses have been paid). Earnings can be 'invested' in a variety of ways, investments that allow for more earnings, investments that protect existing structures, or in investments that are 'frivolous' , i.e., with no obvious benefit. For example, a baker earns an income from the bread he sells. Some of his income he uses for 'maintenance' covering the expenses of his bakery–to buy flour, to pay taxes, to pay for the power to run the ovens, to repair broken machinery, etc.The income left after maintenance costs have been paid can be invested in a variety of ways: (1) investments in additional ovens and mixers or perhaps in a whole new bakery. These investments would increase his earnings and would produce exponential growth. (2) in defenses, such as a sprinkler system to protect his bakery from fire, or perhaps a security system that makes robbery less likely. This might not increase his earnings at all but it does provide for protection against a variety of potential problems. (3) the money could be spent on 'frivolous' items, items that do not protect the bakery. Money might simply be stored under his mattress. Theoretically, plants operate in the same way, material acquired (primarily carbohydrates but also mineral elements) is used for maintenance and what remains can be 'invested' in structures (e.g., leaves)that will allow for the acquisition of more resources, or it might be invested in structures, (e.g., anti-herbivore chemicals), that protect existing structures, or perhaps the material acquired might not have been invested in anything 'worthwhile' at all.Note that as long as the baker(or a plant)invests a set portion of his earnings in ways that increase his capacity to earn more income (even if it is only a very small portion), the result will be exponential growth.
T he exponential model of growth is overly simplistic and usually poorly reflects reality. It does, however, give a starting point from which to analyze growth and the basic idea that as organisms (especially plants) grow , their ability to grow (growth rate) increases simply because they are bigger.