1.4: Organism form- composition, size, and shape
- Page ID
- 70323
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the famous Star Wars bar scene, an attempt was made to illustrate diverse organisms. It was a remarkably unimaginative effort: all of the life-forms illustrated had a striking resemblance to humans, all about the same size and with the same basic components (e.g., head, legs, arms). Without going outside this planet one can come up with a much more diverse set of organisms, as I hope this chapter demonstrates. Organisms vary from each other in multiple ways but in this chapter, I will focus on three aspects, two of which, size and form, are very straightforward, but the third aspect, composition, is less familiar. These characteristics have been shaped by evolution, and e vidence of convergence (unrelated groups converging on a common form) and divergence (related groups showing a variety of forms) abound. Consequently, although form, size and composition are extremely important to an organism 's biology, they are remarkably poor indicators of phylogeny. This makes attempting to characterize the form of larger taxonomic entities (class, order, phylum) challenging, if not impossible. Composition, size, and shape are interrelated and significant to other aspects of an organism' s biology. Moreover, they are also often dynamic, changing during the existence of an organism.

TOPICS
- Composition
- Unicellular
- Multicellular
- Colonial
- Coenocytic
- Size
- Size and shape considerations
- Organism shape: spheres, flattened, cylinders
Composition
What are organisms composed of, i.e., what are they constructed of? A later chapter will consider composition in chemical and molecular terms. In this chapter 'composition' refers to an organism 's cellular nature. Most would agree that all organisms are made of cells, but is it one cell or many? And are the cells all the same or do they differ? And are the cells ' typical' in their organization? Here are four composition types, two of which are very familiar, and two of which are less so:
- unicellular organisms — the organism is a single uninucleate cell
- multicellular organisms ( ' complex multicellularity ' ) — the organism is made of multiple (usually many) cells but the cells are different shapes and have a specific organized arrangement that involves tissues and organs
- colonial composition ( ' simple multicellularity ' ) — the organism is made of multiple cells but the cells are generally similar in size and shape with no obvious tissues and organs
- coenocytic composition — the organism is made of 'atypical' cells, atypical in that they have multiple nuclei, sometimes thousands of them. The entire organism is sometimes just a single cell that has many nuclei, or it may be composed of multiple units, that might be called cells, except that they are generally larger than normal and have multiple nuclei.
Unicellular Organisms
In spite of the fact that plants and animals, the two groups of organisms that most people are familiar with, are multicellular, unicellular composition is by far the most common type of organism. Clearly it is a successful way for an organism to be constructed and most of the 'living' that happens on earth is a consequence of unicellular life. As will be demonstrated by the examples of unicells that are covered here, there is a tremendous diversity in unicellular organisms.

Unicellular organisms are NOT always simple in form and function. They may be very elaborate in form e.g., diatoms (e.g., Thalassiosira ) and dinoflagellates (Figure 2). While any cell is a complex entity, there are many unicellular organisms with components functionally analogous to the (multicellular) organs of more familiar organisms. For instance, Euglena cells possess a remarkable amount of internal organization, including organelles (eye spot, contractile vacuole) that perform functions covered by whole organs (eye, kidney) in multicellular organisms. Also, Euglena (Figure 3) (along with many bacteria and unicellular algae) can move as a result of coordinated re-positioning of extensions that are not multicellular legs, wings or fins but rather an extension of the individual cell called a flagellum ; additionally, Euglena and other unicellular organisms can also move by altering the form of the cellular body, comparable to what earthworms do, but without the aid of muscles and other tissues.
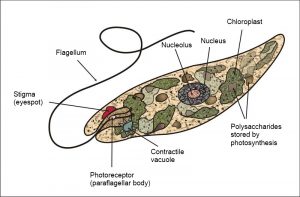
Most organisms go through a stage or stages that is/are unicellular (e.g., spore, gamete, zygote) and these unicells, many of which can be considered organisms because they are often distinct spatially and temporally, are often very elaborate in structure and function. Examples th at will be discussed later are the sperm of multiple groups of plants (e.g., ferns, mosses), often referred to as a spermatozoids (Figure 4).

Although being unicellular is rightfully considered a primitive condition, yeasts are unicellular fungi and demonstrate that the unicellular condition can sometimes 'reappear' in a lineage that previously had some other type of composition, i.e., that unicellularity is sometimes a 'derived' condition. The vast majority of fungi are colonial/multicellular but yeasts have appeared independently multiple times in several different fungal groups and they do NOT represent the primitive condition. In many yeasts the unicellular growth habit is tied to environmental conditions and the organism can be induced to grow in a colonial matter by adjusting conditions.
Colonial Organisms

Colonies of cells (colonial organisms) can form two ways. The less common way is for individual cells to come together to form a colony. This behavior has evolved multiple times, several times in the bacteria (in groups described as 'social bacteria' ) and also in the cellular slime molds like Dictyostelium. (Figure 5) Colonies produced this way will contain cells that are not necessarily all the same genetically. The second and far more common way to form a colony is a result of repeated cell divisions where the daughter cells adhere to their parent. For a cell with a cell wall, the adhesion between daughter cells is accomplished with an adhesive layer deposited between the new cell walls that are produced during cytokinesis.

In colonial organisms, repeated cell divisions produce an organism with many cells attached to each other but the cells are all (or almost all) identical. This type of composition is sometimes described as 'simple multicellularity' or 'plurocellularity' that is distinguished from 'true multicellularity' or 'complex multicellurity' , or sometimes just 'multicellularity' by a variable set of criteria that usually include cellular differentiation and the production of tissues (more on this in the next chapter). A wide variety of colonial forms are possible and result from the patterns in the planes of cell division, e.g., filaments (Figure 6) are formed if the plane of cell division is always the same, producing a chain of cells connected top to bottom.

Filaments can grow from the basal end ( if the original cell continues to divide but the daughter cells do NOT divide) or it can grow from the tip ( if the original cell does NOT divide and the daughter cell repeatedly does divide) or it can grow throughout the filament. F ilament s may branch if some cells in a filament divide in a direction parallel to the direction of the filament; flattened sheets (Figure 7) are produced if cells repeatedly divide in two perpendicular planes; globular cluster s of cells are produced if the original cell and its derivatives divide repeatedly in multiple planes.
Filamentous growth is found in archaea, bacteria, (Figure 8) and fungi and many of the groups that used to be put in the Protist Kingdom, in particular the green, red and brown algal groups and some diatoms. It is also found as a brief stage in most mosses and ferns (Fig 10).


Most fungi exhibit a distinct type of filamentous growth where the filaments, called hyphae, grow from the tip but commonly branch, both at the tip and below it, and with the branches capable of fusing with other hyphae to form what is called a mycelium, an interconnected, anastomosing mass of hypha l filaments (Figure 10).

Two dimensional colonial growth, forming sheets one-to several cells in thickness, is most commonly found in photosynthetic forms, primarily in the algal groups. It also is present in some of the non-vascular plants: all of the hornworts and some of the liverworts (Figure 11), where it presents in the haploid (gamete-forming) form but not the diploid, (spore producing) form (see Chapter 13). Spherical colonies are occasionally found, particularly in the green algae.

The advantages of colonial growth, i.e., of having cells aggregate or having daughter cells remain attached to parental cells, may be different in different situations. One advantage is size; it allows for much larger organisms than a single cell and larger size is sometimes, but not always, advantageous. As discussed below, size affects interaction between organisms and their environment. Colonial growth may be successful because it allows for exploration of the habitat: an organism in a marginal habitat may be sustained as it explores for greener pastures. The larger size of colonies makes possible the exploitation of different habitats/regions. For example, algae are able to exploit both a substrate (for attachment) and the water column (for light and nutrients). Most workers feel that colonial growth (simple multicellularity) is a step on the way to complex multicellularity, but the abundance of highly successful (i.e., diverse and plentiful) colonial forms indicate that colonial growth is itself an advantageous composition type.
Coenocytic Organisms

Probably the least familiar composition type is coenocytic, where the organism's cells, or sometimes its single cell, is multinucleate. This results from mitotic divisions that are unaccompanied by cytokinesis, often repeatedly so. Part of the significance of the coenocytic condition has to do with size. Cell size may be limited because a single nucleus can only control a limited volume of cytosol and for the cell to get bigger there needs to be additional nuclei. Coenocytic cells are usually large and sometimes extraordinarily so. An extreme case is found in the plasmodial slime molds (e.g., Physarum), an amoeba-like organism that consists of a single wall-less cell that may be as much as a meter in length with hundreds of thousands of nuclei (Figure 12). The form of slime molds is dynamic, owing to the ability of the cytoplasm to flow in channels inside the single cell, thereby allowing the organism to explore its environment, engulf food, and even climb up over obstacles. Unlike wall-less plasmodial slime molds, coenocytic organisms with walls can produce specific, permanent forms, but not the way that form is typically created in multicellular organisms (adding cells to create a form), but instead as a result of the creation of shape in individual large cell(s). The bread molds (Rhizopus). produce rhizoids, stolons and stalked reproductive structures, all formed out of a single cell with multiple nuclei (Figure 13).

Similarly, t he notorious invasive green algae Caulerpa , can appear very plant-like, i.e., with 'stem and leaves' , but it's remarkable size and complexity occurs without recourse to cells and tissues.
Many coenocytic organisms are very similar in form to colonial organisms, most commonly filaments but also sheets and spheres. The 'fungal' structure of hyphae/mycelium that is cellular (i.e., colonial) in the sac fungi (Ascomycota ) and club fungi (Basidiomycota) is coenocytic in the bread molds (Zygomycota ) and the mycorrhizal forming Glomeromycota . And this same fungal-like coenocytic form is found in a non-fungus group, the water molds, e.g., the plant pathogen Phytophthora. The structure of water molds explains why the group used to be placed in fungal phylum and also why grouping things by 'looks' , i.e., form, is dangerous! Water molds are now placed in a group that includes brown algae and coccolithophores , two groups that are not at all fungal like nor coenocytic.

Many would not consider these coenocytic organisms to be unicellular, even though technically many are. They are closer to a colonial organism. If one defines organ as a component of an organism that provides a particular function (e.g., anchorage, elevation) then it is apparent that organs can be formed in both colonial and coenocytic organisms (Figure 14), in both cases without the presence of specialized cells and tissues.
Multicellular Organisms
Most workers would not unify all organisms composed of two or more cells as 'multicellular' but developing criteria for useful definitions (e.g., 'simple vs. complex' multicellularity) is challenging and there is no universal agreement as to where to draw lines. For most researchers 'true' multicellularity involves specialization of cell types, a topic that will considered in the next chapter.
Organism Size
Organisms vary tremendously both in volume and their extent in three dimensions. The smallest organisms (Table 1) are prokaryotes (bacteria and archaea), unicellular organisms that lack nuclei or other cellular organelles, with longest dimensions typically of a few um (= 10 -6 mm) and volumes of less than 1 um 3 (= 1 femolitre, where a billion (10 9 ) femolitres equals 1 ul; a quadrillion (10 15 ) femolitres equals 1 litre). These tiny organisms are usually shaped as spheres, rods or spirals. Although most prokaryotic cells range from 0.5 to 10 um, there are a few giant prokaryotes whose cells might be up to 500 um in length, meaning that they can be seen with the naked eye, albeit as a speck.

Unicellular eukaryotes possess cells with nuclei and other cellular organelles. They are generally bigger (10-100 um) than prokaryotes although there are a number of unicellular eukaryotes with small cells, in particular the yeasts (unicellular fungi generally with cells less than 10 um). The fact that unicellular organisms are almost always small in size is generally thought to be a consequence of the need for nuclear control of cellular activity; larger size is difficult because in large cells messages (mRNA, proteins) moving by diffusion take too long to get from the 'control center' (the nucleus, the ribosome) to all parts of the cell. This idea is supported by the following observations:
- coenocytic cells, which have multiple nuclei, are often much larger than cells with a single nucleus
- larger unicells often exhibit cytoplasmic streaming which provides for more rapid movement of signals throughout the cell
- larger unicells (found in plants, fungi and algae) possess a large central vacuole that takes up much of the cell 's volume and that is in some ways a metabolic ' dead space ' that is relatively inactive (or at least not as dynamic as the cytosol); consequently, the amount of cytosol that the nucleus must ' control' is actually much smaller than appears based on cell size
There are a few extremely large unicellular organisms, Acetabularia, (Figure 16) standing up to 5 cm tall, being one of them. Acetabularia is unique not just for its size but also because it demonstrates that 'organs' ( 'rhizoids' , 'stems' , 'leaves' ) are possible even in organisms that are unicellular. Acetabularia cells are over 1000 times larger than typical eukaryotic cells, with maximum dimensions of over 50, 000 um (= 50 mm = 5 cm).

Other large unicells e.g., bread mold ( Rhizopus) , Physarum (plasmodial slime mold) are coenocytic and the case could be made that they really should not be considered unicellular.
Most organisms over 100 um in size are colonial, coenocytic or multicellular. While the cells of coenocytic organism vary greatly in size, the cells of colonial and multicellular organisms are commonly 10 – 100 um in their maximum dimension and the organism 's overall size is determined by how many cells are produced/accumulate. Some of the particularly large organisms that we will consider are: redwoods , up to 85 m in height and weighing an estimated 2100 metric tons (= 2100 * 10 3 kg = 4620 * 10 3 pounds = 2310 tons); giant kelp (brown algae) up to 50 m in length; ' Pando', a clone of trembling aspen that weigh s over 6 million kg, extend s over 43 hectares and may have an age of 80, 000 years (more in the discussion of Populus ); and a honey mushroom (Armillaria) that extends over 4 square miles (1000 hectares), weighs an estimated 55, 000 kg and is considered to be 2400 years old.

Size and shape—influence on surface area & interactions with the environment
Size and shape are particularly significant because they dictate the degree of interaction between the organism and the outside environment. Appreciate that the conditions inside organisms are different from the outside; this is part of what defines life. The second law of thermodynamics (which we will consider in Chapter 24) dictates that differences between the inside and the outside diminish with time: if some chemical is concentrated inside an organism it will tend to leak out; if something is excluded from an organism it will tend to leak in; if an organism is warmer than its environment it will cool; if an organism is cooler than its environment it will warm. Whatever conditions an organism develops to promote its life functions will tend to disappear because the second law dictates that systems change to develop uniformity, i.e., there is a tendency for the inside to become more like the outside. Given this, one might think that having little interaction with the external environment is 'best' . However, interaction with the environment is essential: (1) to obtain materials—food, oxygen, minerals—that are needed to maintain life, and (2) to rid the organism of 'materials' that it produces, e.g. heat and carbon dioxide, that will bring it harm if allowed to accumulate. The size and form of an organism control how it interacts with the environment that it is in. Significantly, size and form affect two important parameters that are related but not exactly the same thing, the surface area of contact with the environment and the volume of the environment in proximitywith the organism. Both of these parameters are important in controlling the interaction between the organism and its environment.
The significance of surface area is familiaridea.More surface area allows for more interaction with the environment, which may or may not be beneficial.For any shape, smaller objects always have a greater surface area per unit volume than large objects(Table 1).
|
shape |
dimension (in arbitrary units) r = radius, s = side |
volume (units3) |
surface area (units2) |
surface area : volume (units-1) |
|---|---|---|---|---|
|
sphere |
r = 0.1 units |
0.004 |
0.126 |
31.5 |
|
sphere |
r = 1.0 units |
4.19 |
12.6 |
3.01 |
|
sphere |
r = 10 units |
4190 |
1257 |
0.3 |
|
cube |
s = 0.1 units |
0.001 |
0.06 |
60 |
|
cube |
s =1.0 units |
1 |
6 |
6 |
|
cube |
s = 10 units |
1000 |
600 |
0.6 |
|
cylinder |
r = 0.1, height = 10 x r |
0.314 |
0.691 |
22 |
|
cylinder |
r= 1.0, height = 10 x r |
3.14 |
69.1 |
2.20 |
|
cylinder |
r= 10, height = 10 x r |
31.4 |
6911 |
0.22 |
|
formulae |
sphere: volume = 4/3 (pi) (r)3; surface area = 4 (pi) (r)2 |
|||
|
cube: volume = (s)3; surface area = 6 (s)2 |
||||
|
cylinder: volume = height (pi) (r)2; surface area = 2 (pi) (r) (height) + 2 (pi) (r)2 |
||||
Keeping volume constant, a sphere has the minimum surface area of any shape, and departures from an isodiametric shape increases the surface area and thus the surface area: volume ratio (Table 2). If one compares the surface area of two common shapes, 'filaments' (elongated in one dimension) and 'sheets' (elongated in two dimensions) while keeping the volume constant, the degree of elongation increases the surface area and elongation in two dimensions has a greater effect than elongation in one dimension (Table 3).
|
shape |
dimensions |
surface area = surface area / volume |
|
sphere |
radius = 0.62 |
4.83 |
|
cube |
side = 1 |
6.0 |
|
cylinder |
diameter = length = 1.08 |
5.49 |
|
shape |
dimensions |
surface area = surface area / volume |
|
thread |
length = 10 x diameter |
8.34 |
|
thread |
length = 100 x diameter |
17.28 |
|
disk |
diameter = 10 x length |
10.32 |
|
disk |
diameter = 100 x length |
40.69 |
|
cuboidal thread |
0.464 x 0.464 x 4.64 |
9.04 |
|
cuboidal thread |
0.215 x 0.251 x 21.54 |
21.73 |
|
cuboidal sheet |
0.215 x 2.15 x 2.15 |
11.09 |
|
cuboidal sheet |
0.0464 x 4.64 x 4.64 |
43.92 |
Consequences of form and size
To see how surface area and form are significantwe will use the example ofthe flow of heat from a warmer environment to a cooler cell, but the same principle would apply to the heat flow from the cell to the environment or the movement of materials, e.g., nutrients into the cell or waste products out ofthe cell. Because smaller objects have relatively more surface area than larger ones, smaller organisms heat up more quickly than larger ones. In fact, because of effective heat exchange between them and their environment, small organisms are always very close to the same temperature as their environment. Only large organisms, with a small surface area to volume ratio, can develop temperatures substantially different from their environment. Considering shape, spherical bodies, withthe least surface area per unit volume, heatmore slowly than any other shape when put in an environment that is hotterthan it; the more deviation from a spherical shapethe faster it will gain heat. If you had three pieces of ice, one spherical, one filamentous and one disc-shaped, all of the same volume, the disk would melt first, then the filament and last the sphere. Assuming equal volumes for ice cubes, the best ice cubes, if you want them to last (not melt), are spherical ones, the best ice cubes if you want them to cool the drink that they are in, are shapes that deviate the most from spheres
A second influence of form: the extent of environment that is explored
An often-overlooked fact is that organisms change their environment around them. In the example just given, the transfer of heat to the cell results in a cooling of theenvironment adjacent to cell. Thecoolingof the environment next to the cell will reduce the gainof heat bythe organismand diminish the significance of surface area to heat transfer. Because of this, a second characteristic related to formbecomes important:the volume of the environment that is within somedistance (the distance depends characteristics of transfer) of the organism. To see why, consider two spherical organisms with a cylindrical 'distortions' of their otherwise spherical boundary: one has an 'outie' (a projection that extends outward), the other has an 'innie' (an invagination that penetrates into the organism) (Figure 18).

As long as the dimensions of the projection / invagination are the same, both the cells will have the same surface area, yet the heat exchange between the 'outie' cell will be faster than that from an 'innie' cell. This is because the conditions of the environment inside the 'innie' projection will become more similar to those of the organism than to the conditions of the bulk environment outside of the cell. The volume of 'the environment' that is in the 'innie' is small and the surface area between the innie and the cell is relatively large, consequently as the 'innie' part of the environment loses its heat to the cell it would become less and less significant a source of heat. Thus, the additional surface area resulting from the 'innie' would become of little consequence in terms of interacting with the environment. In contrast, the additional surface area of the 'outie' can remain more effective in facilitating heat transfer because this area is surrounded by the environment, not the cell. Hence surface area by itself is not always the best measure of how much interaction an organism (or object) might have with its environment.
A consequence of this is that form is important in influenc ing the transfer of materials between the organism and the environment in two ways: (1) by determining surface area of a given volume of organism, and (2) by influencing the volume of the environment that is in close contact with the cell. Although an 'innie' does increase surface area, this does little to influence the volume of environment close to a cell; an 'outie' does much more. The significance of how much of an environmental volume is explored depends on several factors including the rate at which heat or material is conducted through the environment and the rate at which heat or material can be transferred from the environment to the organism. If the environment transfers heat or material readily, or if the rate of transfer into the cell is slow, the importance of how much environment is explored is of less importance.
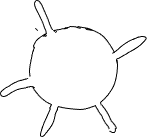
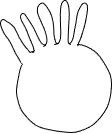
Consider another example of two cells with the same number of multiple outies, extensions outward, and the same surface areas. One has the outies close together, the other has them spaced out (Figure 19). The cell with spaced out extensions explores more of the environment than the other and will be able to acquire more heat or material from its environment (or lose more heat or material to its environment), especially if the rate at which heat or materials move through the environment is relatively slow, or the rate at which they are absorbed/lost is relatively fast. A parameter can be calculated that is the volume of environment within some distance of the cell surface; outies that are close to each other are less effective in increasing the amount of environment being 'accessible' than are more separated outies.
Some (perhaps) familiar situations demonstrate the importance of form and some of the complications related to it. The microvillae, small projections of small intestine that extend out into the gut track, are often cited as being important in the absorption of materials from the gut because they provide increased surface area. This is certainly the case but it should also be pointed out that the movement of material through the gut track, a result of peristalsis, is what allows the additional surface area to be significant. If not for peristalsis continually bringing 'fresh' material to the dense stand of microvillae, the increased surface area would be of little utility. Peristalsis changes the environment next to the microvillae. Root hairs, cylindrical extensions from the cells on the outside of roots, are another situation where increased surface area is cited as being significant to the water absorption function of roots. This may not always be the case, especially when the root hairs are extremely dense and if water is abundant, which allows it to move more readily through the soil. However, roots and root hairs don't just absorb water, they also acquire nutrients and the impact of root hairs may be different for different nutrients compared to the impact for water. Moreover, the conductivity of the soil to water and minerals is very strongly affected by how much water is present, a very dynamic property for most soils. Root hairs probably do multiple things that are significant for absorption of water and minerals: (1) increase surface area, (2) increase the volume of soil in close proximity to the root, (3) improve contact between the root and the soil by preventing gaps (air spaces) which would drastically reduce absorption of water and nutrients, (4) perform metabolic functions that facilitate nutrient absorption, e.g., active transport.
Shapes of Organisms
While there are a wide variet y of shapes of organisms, three common forms are cylinders, sheets and spheres. Many organisms are composites of different shapes, i.e., they have some pieces that are one shape and other pieces that are another shape, e.g., m any animals have cylindrical appendages attached to a spherical core. M ost above-ground plants are composed of flattened sheets ( leaves ) attached to cylindrical stems. Both the above-ground and below-ground form of plants typically are filaments that branch repeatedly, a form that is also found in fungi. Common forms for the organisms covered in this text are outlined in the Table 4.
|
shape |
examples |
notes |
|---|---|---|
|
spheres |
many unicellular organisms, some colonial and multicellular ones |
low surface area to volume ratio and small amount of environmental volume explored per unit of organism |
|
flattened |
many colonial and multicellular algae including sea lettuce (Ulva) and kelp (Laminaria); the haploid form of all hornworts and many liverworts |
high surface area to volume ratio, often significant for photosynthetic organisms to absorb more light |
|
cylinders (branched or unbranched) |
most fungi, many green and red algae, some bacteria, the roots of vascular plants |
both a high surface area to volume ratio and potentially a large amount of environmental volume explored per unit of organism |
|
cylinder with (non-cylindric) appendages |
some macroalgae (red, brown and green); most plants–including most mosses, many liverworts and almost all vascular plants |
the appendages typically are flattened and photosynthetic and their shape increases the amount of surface area exposed to light |
Spheres
As mentioned above, spheres have a minimum surface area per unit volume. Assuming that there is a specialized boundary on the outside of the object, be it unicellular or multicellular, a sphere would require the minimum amount of boundary, which often is composed of relatively expensive materials. Spherical shapes are also more mobile in many situations owing to their reduced drag, which in general increases with surface area. While there are a number of roughly spherical animals, spherical multicellular organisms from other groups, in particular, the groups we are covering, are uncommon. However, the form is commonly found organisms that are unicellular: many bacteria, many unicellular green algae, dinoflagellates, cryptophytes and coccolithophore are roughly spherical in shape and the shape occasionally occurs in colonial organisms (some green algae). Spheres are also common in dispersal units: pollen, seeds, spores, all of which are entities that might be considered organisms. And spherical shapes are also a common shape for the structures (organs) that contain elements to be dispersed: sporangia (spore containers), fruits (seed containers), anthers (pollen containers). The advantage(s) of spherical shapes no doubt varies on circumstances and may also reflect other constraints on development. In rare occasions, round shaped seeds, fruits and even whole plants may aid in the dispersal of propagules by wind and gravity. A whole-plant example of the this is the tumbleweed, whose spherical shape promotes the dispersal by the wind of the seeds which are released from the rolling plant. Spherical forms are typical of the (usually underground) storage organs of flowering plants: corms, bulbs and tubers and this is probably a consequence of surface area to volume considerations.
Flattened structures
Flattened structures are especially common in photosynthetic organisms, undoubtably because of the importance of intercepting light. While it is often stated that flattened shapes 'intercept more sunlight' than other shapes (e.g., maple leaves vs. pine needles), this is misleading; similar amounts of light can be acquired given any particular shape. What is significant is how much volume is required to produce a given area of light absorbing surface, and also how much total surface area is required. Table 5 compares morphological characteristics for three different leaf shapes: cubes, sheets and filaments. In each situation the assumption is made that one 'face' of the shape is facing the light source and that light absorption only occurs on this surface. As can be seen the same amount of light could be intercepted by ten cuboidal leaves, each 10 x 10 x 10 cm in size, or ten filamentous leaves, each 100 x 1 x 1 cm or by ten planar leaves 10 x 10 x 1 cm. While both filaments and planar leaves can produce the same amount of absorbing surface per unit volume of leaf, cuboidal leaves 'cost' much more (illuminated area: total volume) (Table 5). The difference between filamentous leaves and planar leaves is that planar leaves reduce the total surface area required to produce a given amount of absorptive surface. It is probably these two factors that are significant in ensuring that light absorbing surfaces are generally planar: thick leaves require volume that cannot be used effectively for photosynthesis; filamentous leaves produce excess total surface area which may be costly in terms of other factors, e.g., water loss for terrestrial organisms.
The flattened structure may be the entire organism (some green, red and brown algae, some liverworts (including Marchantia , hornworts ) or, most commonly, the flattened structures occur as leaves / leaf-like structures off of a cylindrical stem.
|
shape |
number of leaves |
dimensions |
total volume |
total surface area |
illuminated area / total area |
illuminated area / volume |
|
cuboidal |
10 |
10 x 10 x 10 |
10000 |
6000 |
1 / 6 |
1: 100 |
|
filamentous |
10 |
100 x 1 x 1 |
1000 |
4020 |
1 / 4.02 |
1 : 1 |
|
planar |
10 |
10 x 10 x 1 |
1000 |
2400 |
1 : 2.4 |
1 : 1 |
Certainly, the above treatment is superficial and some complicating factors should be noted: light is usually not only absorbed by one surface of any structure as the sun 's position changes during the day and season; light penetrates through a surface to layers below; although most leaves move only minor amounts during the day or season, some leaves change position to ' track ' the sun; and some leaves change position to reduce solar exposure. And, in spite of the trend of generally planar light absorbing surfaces, there are multiple examples of filamentous ' leaves ' and also examples of spherical' leaves.'
A planar shape is also sometimes found in propagules, the dispersal stages of organisms, where the flattened 'wing' aids in dispersal in the air. Interestingly, wings are primarily found in relatively large propagules, the seeds and fruits of seed plants, with dimensions greater than a few millimeters. 'Wings' are uncommon in aquatic organisms and in small propagules: e.g., spores and pollen. Although most conifer pollen has two 'wings' , they are not particularly flattened and, in spite of the fact that conifers are wind pollinated, the role of the wings may not be to aid in dispersal but rather to orient the pollen grain after it has been dispersed.
Cylindrical structures

Cylindrical structures are extremely common, both as parts of organism and as the whole organism. Cylindrical unicellular organisms are found in rod-shaped bacteria and archaea; filamentous colonial forms are represented by some bacteria, many cyanobacteria, colonial diatoms, many green algae and some red and brown algae. For most of these colonial organisms, the filaments are all one cell thick, but, especially in the red and brown algae, the filaments may be thicker, often several cells thick. There are many coenocytic green algae that are filamentous.

A branched filamentous structure is particularly effective as a 'feeding' (for fungi) or 'mining' structure (for plant roots) that explores an environment for resources. Such a form is also effective in providing anchorage because it allows for extensive interaction between the organism and its substrate. In contrast to roots, which have dual functions of absorption and anchorage, the holdfasts of algae and rhizoids of mosses, liverworts and hornworts perform little absorption but primarily serve an anchorage role. Across the diversity of organisms, what it is that forms the branched structure and the size of the branched structure vary tremendously. Unicellular chytrids (fungi) form 'rhizoids' for absorption and anchorage that are extensions of a single cell. The 'arbuscules' (literally meaning 'little tree' ) of Glomeromycota fungi are also extensions of parts of the fungal cell that enters into plant root cells. Root hairs are also extensions of individual cells. The rhizoids of mosses, liverworts and hornworts are usually a filament made up of a string of individual cells. Holdfasts of macroalgae and the roots of plants (as opposed to root hairs), are multicellular and made up of multiple cells.
Cylinders with non-cylindrical appendages
Cylinders also function to position organs in favorable locations, e.g., the stem of plants or the stipe of the larger algae, distributing flattened leaves/leaf-like structures in order to obtain more light. The vast majority of plants, ranging from mosses, most liverworts and all vascular plants, have an above-ground structure that can be described as a 'stem with leaves' . Typically, the cylindrical stem branches and is erect but sometimes it is unbranched and sometimes it is prostrate, running along the ground surface.
Phytopthora, a water mold, is a parasite that grows inside plant leaves and produces branched structures that emerge from the leaf through stomates, regulated pores in the leaf surface, and form cylindric, branched structures upon which are produced reproductive structures which are dispersed.
Cylinders (stalks) also repeatedly serve to elevate structures that are producing propagules (mobile reproductive structures) and thereby facilitate dispersal of propagules. T he ubiquity of the structure reflects the structure 's significance in multiple situations over quite a range of size s: from stalks as short as 1 micron in myxobacteria, to 1 millimeter in slime molds, to 1 centimeter in mosses, to meters in height (flowering plants). The cylindrical stalks can be parts of a cell (bread molds, some slime molds), made of a single filament of cells (fungi), a collection of intertwining filaments (fungi) or truly multicellular (some fungi, mosses, vascular plants). Generally, such structures are found in terrestrial organisms with stalks that carry propagule-producing-structures upward into the air. Apparently even a very short upward extension can enhance dispersal by allowing the propagules to be released above the most sedentary part of the boundary layer, the layer of still air that blankets all objects, and in particular the ground. Apparently, such structures are not as advantageous in aquatic situations because they are much less common. In some situations, a stalk is significant not by moving the propagule-producing-structure up (relative to gravity) but because it moves the structure outside of the organism' s own body or outside the body that it is growing inside of (e.g., fungi, some parasites).

As the last example demonstrates, cylinders are significant to a number of organisms as a means of mobility, to arrive at new places. Although most of the organisms that we study are considered immobile, they are capable of movement that is due to growth, and a cylinder is an effective structure to cover territory. Examples include: horizontally running above ground stems (stolons) and below ground stems (rhizomes) of plants, the 'stolons' of bread molds, rhizomorphs of fungi, horizontal 'runners' in Caulerpa , a green alga.


