4.5.1.3: Cohesion-Tension Theory
- Page ID
- 32037
Learning Objectives
- Explain how water moves upward through a plant according to the cohesion-tension theory.
- Provide experimental evidence for the cohesion-tension theory.
In 1895, the Irish plant physiologists H. H. Dixon and J. Joly proposed that water is pulled up the plant by tension (negative pressure) from above. As we have seen, water is continually being lost from leaves by transpiration. Dixon and Joly believed that the loss of water in the leaves exerts a pull on the water in the xylem ducts and draws more water into the leaf. But even the best vacuum pump can pull water up to a height of only 10.4 m (34 ft) or so. This is because a column of water that high exerts a pressure of 1.03 MPa just counterbalanced by the pressure of the atmosphere. How can water be drawn to the top of a sequoia, the tallest is 113 m (370 ft) high? Taking all factors into account, a pull of at least ~1.9 MPa is probably needed.
The answer to the dilemma lies the cohesion of water molecules; that is the property of water molecules to cling to each through the hydrogen bonds they form (Figure \(\PageIndex{1}\)). When ultrapure water is confined to tubes of very small bore, the force of cohesion between water molecules imparts great strength to the column of water. It has been reported that tensions as great as 21 MPa are needed to break the column, about the value needed to break steel wires of the same diameter. In a sense, the cohesion of water molecules gives them the physical properties of solid wires.

According to the cohesion-tension theory, transpiration is the main driver of water movement in the xylem. It creates negative pressure (tension) equivalent to –2 MPa at the leaf surface. Water from the roots is ultimately pulled up by this tension. Negative water potential draws water from the soil into the root hairs, then into the root xylem. Cohesion and adhesion draw water up the xylem. Transpiration draws water from the leaf through the stoma. Water potential becomes increasingly negative from the root cells to the stem to the highest leaves, and finally to the atmosphere (Figure \(\PageIndex{2}\)).

The water potential at the leaf surface varies greatly depending on the vapor pressure deficit, which can be negligible at high relative humidity (RH) and substantial at low RH. At night, when stomata typically shut and transpiration stops, the water is held in the stem and leaf by the adhesion of water to the cell walls of the xylem vessels and tracheids, and the cohesion of water molecules to each other.
The mechanism of the cohesion-tension theory is based on purely physical forces because the xylem vessels and tracheids are not living at maturity. Evaporation of water into the intercellular air spaces creates a greater tension on the water in the mesophyll cells , thereby increasing the pull on the water in the xylem vessels. The xylem vessels and tracheids are structurally adapted to cope with large changes in pressure. Rings in the vessels maintain their tubular shape, much like the rings on a vacuum cleaner hose keep the hose open while it is under pressure. Small perforations between vessel elements reduce the number and size of gas bubbles that can form via a process called cavitation. The formation of gas bubbles in xylem interrupts the continuous stream of water from the base to the top of the plant, causing a break termed an embolism in the flow of xylem sap. The taller the tree, the greater the tension forces needed to pull water, and the more cavitation events. In larger trees, the resulting embolisms can plug xylem vessels, making them non-functional.
The pulling force due to transpiration is so powerful that it enables some trees and shrubs to live in seawater. Seawater is markedly hypertonic to the cytoplasm in the roots of the red mangrove (Rhizophora mangle), and we might expect water to leave the cells resulting in a loss in turgor and wilting. However, the remarkably high tensions in the xylem (~3 to 5 MPa) can pull water into the plant against this osmotic gradient. Mangroves literally desalt seawater to meet their needs.
Experimental evidence supports the cohesion-tension theory. Over a century ago, a German botanist who sawed down a 21-m (70-ft) oak tree and placed the base of the trunk in a barrel of picric acid solution. The solution was drawn up the trunk, killing nearby tissues as it went. If the roots were the driving force, upward water movement would have stopped as soon as the acid killed the roots. However, the solution reached the top of the tree. When the acid reached the leaves and killed them, the water movement ceased, demonstrating that the transpiration in leaves was causing the water the upward movement of water.
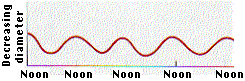
According to the cohesion-tension theory, the water in the xylem is under tension due to transpiration. Consistent with this prediction, the diameter of Monterey pines decreases during the day, when transpiration rates are greatest (Figure \(\PageIndex{3}\)). Because the water column is under tension, the xylem walls are pulled in due to adhesion.
The Tallest Trees
By spinning branches in a centrifuge, it has been shown that water in the xylem avoids cavitation at negative pressures exceeding ~1.6 MPa. And the fact that giant redwoods (Sequoia sempervirens, Figure \(\PageIndex{4}\)) can successfully lift water 109 m (358 ft), which would require a tension of ~1.9 MPa, indicating that cavitation is avoided even at that value. However, such heights may be approaching the limit for xylem transport. Measurements close to the top of one of the tallest living giant redwood trees, 112.7 m (~370 ft), show that the high tensions needed to transport water have resulted in smaller stomata, causing lower concentrations of CO2 in the needles, reduced photosynthesis, and reduced growth (smaller cells and much smaller needles; Koch et al. 2004). The limits on water transport thus limit the ultimate height which trees can reach. The tallest living tree is a 115.9-m giant redwood, and the tallest tree ever measured, a Douglas fir, was 125.9 m.

Reference: Koch, G., Sillett, S., Jennings, G. et al. The limits to tree height. Nature 428, 851–854 (2004). https://doi.org/10.1038/nature02417
Supplemental Reading
Woodward, I. Tall storeys. Nature 428, 807–808 (2004). https://doi.org/10.1038/428807a
Attributions
Curated and authored by Melissa Ha using the following sources:
- 30.5 Transport of Water and Solutes in Plants from Biology 2e by OpenStax (licensed CC-BY). Access for free at openstax.org.
- 16.2A Xylem from Biology by John. W. Kimball (licensed CC-BY)


