5.2: Spectrophotometry
- Page ID
- 18148
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The human eye responds to electromagnetic radiation within a range of wavelengths between 400-750 nm (i.e. the "visible spectrum"). Samples of light that contain a continuous spectrum of all wavelengths between 400-750nm will be perceived by the brain as "white light" (e.g. the sun). Light comprising a specific wavelength within this range is perceived by the brain as being "colored":
|
|
|
|
|
|
Often objects appear colored because of their absorption of light within selective regions of the visible spectrum. The light from such objects that strikes our eyes (whose color we perceive) is composed of those wavelengths that the object DID NOT absorb.
For example, plant leaves contain two photosynthetic pigments: chlorophyll A and chlorophyll B. The chlorophyll A molecule has the ability to absorb light with a wavelength in the range of 430 and 660 nm; the chlorophyll B molecule absorbs light with a wavelength in the range of 450 and 640 nm. Thus, these two pigments in leaves absorb violet/blue and orange/red wavelengths of light (the energy that these photons represent is transferred to the chlorophyll molecules). Light with wavelengths in the range of 500-600nm is not absorbed by either molecule. Thus, after sunlight interacts with leaves the wavelengths that remain (and that our eye can perceive) are green-yellow. Therefore, plants are "green" because they don't absorb green light.
- What would an object look like if it contained a pigment that absorbed all wavelengths from 400-750nm? It would be "black"
- This is the same situation as being in a closed room with the lights turned out. Without light there is no color.
If we had a sample of leaf juice containing chlorophyll A and B we could quantitate the concentration of chlorophyll by the amount of violet/blue and orange/red light it absorbed. We COULD NOT quantitate it by the amount of green light transmitted (it would be essentially the same amount regardless of the amount of chlorophyll:
.png?revision=1&size=bestfit&width=378&height=168)
Figure 5.1.1: Chlorophyll light transmission
Even though the sample is "greener" with higher concentrations of chlorophyll, this is not due to an increase in the intensity of the green wavelength of light; it is due to a reduction in the violet/blue and orange/red wavelengths of light. It is this reduction that we can use to quantitate the concentration of chlorophyll. Although the sample appears green we cannot quantitate it by monitoring the green wavelength of light.
Light, Energy and Molecular Structure
Light is strange stuff, it is a radiative form of energy transfer, and in order to understand its properties we have to consider it to have both wave and particle properties. The different wavelengths of light differ in the energy they carry; the energy is directly proportional to the frequency of the light (the higher the frequency, the higher the energy):
E α n
The energy unit is the erg (1Joule = 107ergs) and the frequency unit is Hertz (i.e. cycles per second, or just units of sec-1). The constant of proportionality is Planck's constant, h, with a value and units of 6.6 x 10-27 erg sec
E = hn
erg = (erg sec)(sec-1)
The frequency (n) of light is inversely proportional to the wavelength (l):
n α 1/λ
Frequency has units of sec-1 and wavelength has units of meters. The constant of proportionality is c (the speed of light) with a value and units of 3 x 108m/sec:
n = c(1/λ) = c/λ
This relationship is true in a vacuum; however, "optically dense" materials can slow the speed of light requiring the following correction to the above equation:
n = c/nl
where n is the "refractive index" of the material and has a value > 1
Therefore, the energy of light is inversely proportional to the wavelength:
E = (hc)/(nl)
The "photon" is a corpuscular (particle) description of light that is the carrier of the "quanta" of energy defined in the above equation. When light is absorbed by a molecule it transfers its quanta of energy, and the photon ceases to exist. Where did the energy go?
- The atomic bonds, chemical structure and electrons of a given molecule have specific excited states and vibrational modes.
- These excited states and vibrational modes have defined energy levels above the ground state.
- The molecule can change from the ground state to an excited state (or vibrational mode) upon the absorption of a quanta of energy exactly equal to the difference between the ground and excited states.
- Thus, molecules can absorb the energy associated with specific wavelengths of light, and the light is consumed in the process.
.png?revision=1&size=bestfit&width=367&height=329)
Figure 5.1.2: Scale of light
The atomic bonds, chemical and electronic structure of molecules are unique properties and differ from one type of molecule to another.
- Thus, the energetic differences between the ground and excited states differs from one type of molecule to another.
- Therefore, the ability to interact and absorb light, and the specific wavelengths of light absorbed differ from one type of molecule to another
The characteristic absorption pattern of the different wavelengths of light is unique for each type of molecule and is a type of molecular "fingerprint" that can be used to identify and quantitate molecules
In the example of chlorophyll given above the intensity of light passing through the sample is termed the "light transmittance" of the sample:
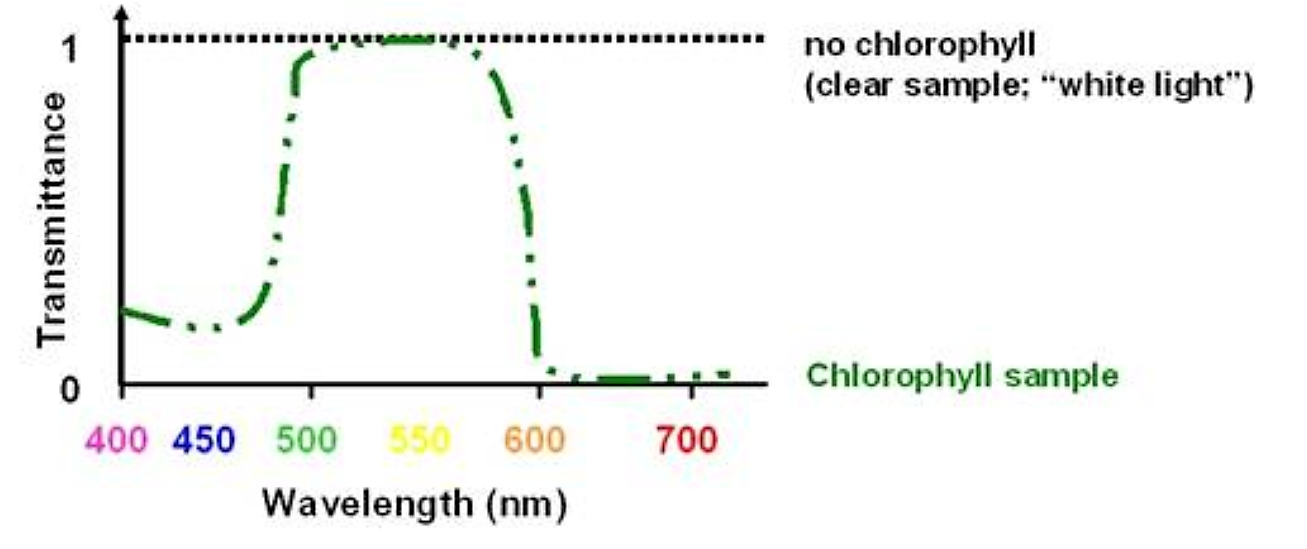.png?revision=1&size=bestfit&width=475&height=200)
Figure 5.1.3: Light transmittance of chlorophyll
- Transmittance is a dimensionless number that varies from 1 (full transmittance) to 0 (no transmittance - complete absorption)
It is important to note the distinction between transmittance and absorption: they are inversely proportional
- A sample with high absorbance has a low transmission of light
.png?revision=1&size=bestfit&width=457&height=226)
Figure 5.1.4: Chlorophyll absorption
How are transmittance (T) and absorption (A) quantified?
- The intensity of light shining on a sample is termed the incident light, I0
- The intensity of light measured after passing through a sample is the transmitted light, I
- Transmittance, T, is defined as the ratio I/I0 and will vary between 0 and 1:
.png?revision=1&size=bestfit&width=352&height=258)
Figure 5.1.5: Transmittance
How is the transmittance affected by the sample concentration and physical size (i.e. path length)?
- If the transmittance is reduced due to the absorption by the sample, then the higher the concentration (c), the lower the transmittance. In other words, the transmittance is inversely proportional to the concentration: (Beer's law)
T α 1/c
- Similarly, the thicker the sample (i.e. the greater the path length of the light through the sample), the lower the transmittance. Thus, the transmittance is also inversely proportional to the path length (l): (Lambert's law)
T α 1/l
Thus, we expect the equation relating T to c and l to take the general form of:
T α 1/cl
Transmittance turns out to decrease exponentially with increases in the concentration and path length, thus the equation has the form:
logT α 1/cl
-logT α cl
The constant of proportionality is the extinction coefficient e:
-logT = εcl
Since log values are dimensionless, the units of e would appear to be inverse concentration and inverse distance (e.g. M-1cm-1)
The -logT term on the left can be written as log(1/T) and identifies the inverse relationship between the transmittance T and the ecl term. Since absorbance and transmittance are inversely related, the ecl term would seem to be a convenient definition for the absorbance (A):
log(1/T) = ε cl = A
(the Beer-Lambert Law)
Values for ε and l
- Path length l is usually in units of cm
- Molar extinction coefficient ε has units of M-1 cm-1 and is a constant of proportionality that relates the absorption of molar solutions
- Mass extinction coefficient ε 1% refers to the absorbance of a 1% by mass solution. Typically this refers to an aqueous solution that we can take to have a density of 1000g/L. A 1% by mass aqueous solution would therefore refer to the dissolution of 10g/L, or a 10mg/ml solution of the molecule of interest.
- Since the absorbance of a molecule is a function of the wavelength (i.e. the absorption is not equal for every wavelength) the extinction coefficient must also reference a wavelength. This is typically done using a subscript:
ε 1%280nm = 14.5 g-1 L cm-1
· In this case a 10mg/ml solution of the molecule will have an absorbance reading of 14.5 (dimensionless units) at l = 280nm (the absorption at other wavelengths may not be known). The units of concentration are g/L, thus e will have dimensions of g-1 L cm-1.
The relationship between changes in A, T and c
· The direct relationship between A and c means that there is a linear relationship between absorbance and concentration. If you double the concentration the absorbance will double, etc.
· The inverse log relationship between transmittance and absorbance can be stated as:
T = 1/10A
- A doubling of the concentration will therefore result in a 10-fold reduction in the transmittance. Instrumentation for absorbance measurements (spectrophotometers) actually measure transmittance, and naturally become less accurate at low values of transmittance. Thus, the higher the absorbance reading the less accurate it is. Most such instrumentation is inaccurate at absorbance readings > 1.5 (this works out to be at transmittance < 3% of full transmittance)
Design of Spectrophotometers
Spectrophotometers are precision instruments, however, conceptually they involve a relatively few number of parts. A simple design would look something like this:
.png?revision=1&size=bestfit&width=506&height=354)
Figure 5.1.6: Spectrophotometer
- A tungsten lamp is used to produce wavelengths of light spanning the visible range, while a deuterium lamp is used to produce light spanning the ultraviolet range.
- The movable prism or diffraction grating is adjusted to direct the wavelength of interest towards the sample
- This is a "single beam" spectrophotometer and the reference and sample data are collected separately (the reference sample is used to determine the maximum transmission value (effectively I0)
A modification of this design, a "dual beam" spectrophotometer, can permit simultaneous measurement of I and I0:
.png?revision=1&size=bestfit&width=561&height=467)
Figure 5.1.7: Dual beam spectrometer
Both the single and dual beam detectors allow the investigator to monitor the absorbance properties for a single wavelength of light (the wavelength selected by the prism/slit settings. A modification that incorporates an array of detectors can permit simultaneous measurement of a spectrum of wavelengths:
.png?revision=1&size=bestfit&width=514&height=387)
Figure 5.1.8: Simultaneous measurement of a spectrum
Absorbance spectra of biological molecules
Proteins
Proteins do not absorb in the visible wavelength unless they have a prosthetic group (e.g. Fe2+) or an unnatural amino acid. However, the amino acids tryptophan, tyrosine and cysteine absorb light in the UV wavelength:
.png?revision=1&size=bestfit&width=385&height=333)
Figure 5.1.9: Tryptophan absorption
- Tryptophan has a peak of absorption at 280nm in the UV range
- This is a useful wavelength to quantitate the absorption of tryptophan
- Since the absorption is proportional to concentration, this is a useful way to quantitates protein concentration (for proteins containing Trp)
Nucleic acids
The aromatic rings in the bases of nucleic acids also absorb in the UV range:
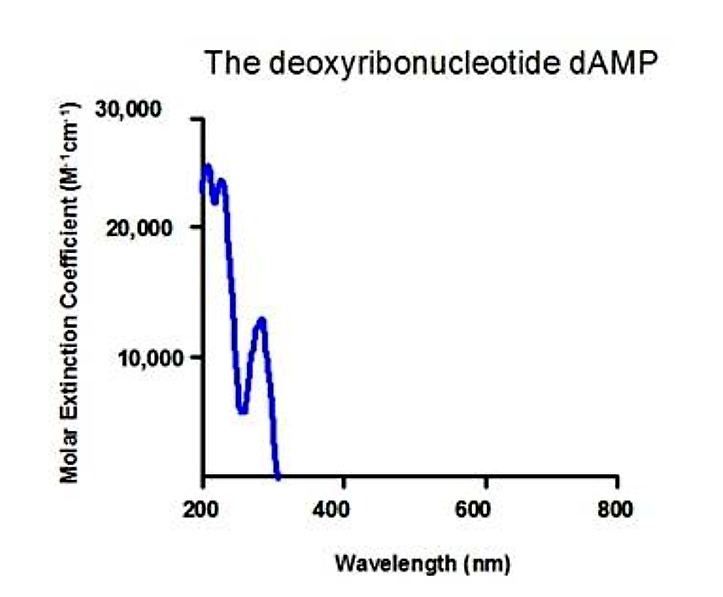.png?revision=1&size=bestfit&width=387&height=320)
Figure 5.1.10: Nucleic acid absorption
- Each DNA and RNA base has a slightly different absorption spectrum
- 260 or 280nm is a typically useful wavelength to monitor concentration of nucleic acids
Note that samples of nucleic acids and proteins can both absorb at 280nm, therefore, samples of biological molecules should be pure in order to quantitate using UV absorption spectroscopy.


