2.4: Solubility in an aqueous world - noncovalent interactions in depth
- Page ID
- 42289
Introduction
In section 2.1, we explored the role of water as a solvent. Using the adage "like dissolves like" that you may have learned in introductory chemistry and biology courses, we can rationalize what substance might dissolve in water. We related this to the types and strengths of attractive interactions that occur between solute and solvent. If in sum they are stronger than self-interactions (solute-solute and solvent-solvent), the solute would dissolve (to a reasonable extent) in the solvent. We also discussed entropic contributions to the dissolution process. For now, we will refocus on the noncovalent interactions.
In introductory science courses, noncovalent interactions are often described as intermolecular forces. This term is ambiguous when applied to biochemistry. Take for example hydrogen bonds. They occur between two water molecules, for example, but also within larger molecules (like proteins) if hydrogen bond donors and acceptors within the molecule get close enough to each other in space.
The table below summarizes the common noncovalent interactions/“intermolecular forces” that you studied in introductory science classes. It is hard enough for students to recognize and identify these interactions between two small molecules let alone in large molecules like proteins. We will explore these in more detail below, and give examples of noncovalent interactions between small molecules and within large ones such as proteins. We'll also add a few more specific examples of interactions.
Noncovalent Interactions - "Intermolecular Forces"
|
Interaction Type |
Example |
Distance |
Relative Strength Kcal/mol (kJ/mol) |
Direction Dependence |
| Ion-Ion | 1/r | 60 (250) | nondirectional | |
| H-Bond | 3-15 (12-63) | directional | ||
| Ion-dipole | 1/r2 | 3-5 (12-21) | directional | |
| Dipole-dipole | 1/r3 | 0.5-1 (2-4) | directional | |
|
Induced Dipole- Induced Dipole |
1/r6 |
0.5 (2) (depend on size) |
nondirectional |
Although there are many different types of noncovalent interactions, one fundamental principle governs all of them. They all originate in the electrostatic force between two charged objects. There is one simple law, Coulomb’s Law, which you would have discussed in introductory science courses, and one simple equation, that describes the electrostatic force:
\begin{equation}
F=\frac{k Q_1 Q_2}{r^2}
\end{equation}
where F is the force (attractive or repulsive) between two particles of charge Q1 and Q2 with their centers separated by some distance r. Replace the charges with the masses of two objects and you have Newton's Law of Gravitation. Both are inverse squared laws
All the interactions described in the table above arise from the electrostatic force. The magnitude of the attractions for the interactions depends on the way charge is distributed in the attracting species. Each has a different dependency on distance.
Different words are used to describe noncovalent interactions. This can be distressing to learners who might hear different terms used by chemists and biologists for the same noncovalent interactions. Some use van der Waals forces to describe induced dipole-induced dipole interactions, while others use London dispersion forces or hydrophobic forces/interactions. Others use van der Waals forces to describe all noncovalent interactions except for ion-ion. To avoid ambiguity, let's look at the IUPAC Gold Book Compendium of Chemical Terminology, which offers this definition of van der Waals forces:
"The attractive or repulsive forces between molecular entities (or between groups within the same molecular entity) other than those due to bond formation or to the electrostatic interaction of ions or of ionic groups with one another or with neutral molecules. The term includes: dipole–dipole, dipole-induced dipole, and London (instantaneous induced dipole-induced dipole) forces. The term is sometimes used loosely for the totality of nonspecific attractive or repulsive intermolecular forces". IUPAC. Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). Online version (2019-) created by S. J. Chalk. ISBN 0-9678550-9-8. https://doi.org/10.1351/goldbook.
Figure \(\PageIndex{1}\) summarizes covalent and noncovalent interactions, using that definition.
Using this definition, hydrogen bonds are usually considered a type of dipole-dipole interaction. Historically, several of the noncovalent interactions have alternative names based on the person associated with them. Only the names van der Waal and London are commonly used in introductory chemistry courses
Even the word "force" is potentially ambiguous. To a physicist, there are only four known forces:
- gravitational, between two objects with mass
- electromagnetic (between static charges - the electrostatic force, and moving charges - the magnetic force)
- the strong force (holding the nucleus together)
- the weak force (also nuclear and involved in radioactive decay).
We'll try to use the word interaction throughout this book.
Interactions within small molecules, such as covalent bonds, and between molecules, such as induced dipole-induced dipole, vary as some function of r, the distance between the two interacting particles. Only ion-ion interactions vary as 1/r2 (F= k/r2). Attractions lower the overall energy while repulsions raise it. At some optimal distance, the system is in its most favored, lowest energy state.
We just switched from discussing forces to discussing energy, another complex term. The relationship between the potential energy for covalent bond formation and for the noncovalent attraction of two atoms as a function of distance is shown in general form in Figure \(\PageIndex{2}\): below.
Figure \(\PageIndex{2}\): Potential Energy for Covalent and Noncovlanet interactions
The curve in black shows the shape of Epot vs r for the formation of a covalent bond between H atoms. The Morse potential energy function is used to model energy as a function of r for simple diatomic molecules. The red line shows the shape of Epot vs r for the noncovalent attraction of two He atoms through induced dipole-induced dipole interactions. It is modeled using the Lennard-Jones (6-12) potential function (see below). Each has an optimal r0 (the bond length for H2 and two times the van der Waals radius, rW, of each He in 2He). The energy required to break the induced dipole-induced dipole interactions between He atoms is very small, which accounts for the fact that liquid He, in which many He are interacting, only exists at very cold temperatures (boiling point = -269 Celsius).
Although the graph for H2 shows the relationship between the potential energy and r0 for the covalent bond, in reality, the sources of stability of any covalent bond are complex and require, in addition, a term for the kinetic energy of the electron. Fundamentally, the strength of a covalent bond is best described using quantum wave functions for the system. The average single covalent bond strength depends on the atoms bonded and varies between 30-120 kcal/mol (125-500 kJ/mol), a factor of 4.
Another confusing feature when discussing noncovalent interactions is that while we talk about forces (like the electrostatic force), we often draw graphs of energy E vs r, the distance between two interacting particles. Let's briefly examine the relationship between potential energy (Epot) and force for the electrostatic force given by Coulomb's Law by using a more familiar example, the next gravitational force of a stationary ball placed at various points on a hill, as illustrated in Figure \(\PageIndex{3}\).
Assume the ball is motionless at each position in the diagram so only potential energy can be considered. The red arrows (vectors) represent the relative net downward force on the ball at each position. The net downward force at the top and bottom of the hill is zero. As the slope of the hill increases, the net downward force increases. The force is directly proportional to the slope (dE/dr), or simply:
\begin{equation}
F=-\frac{\Delta \mathrm{E}}{\Delta \mathrm{r}}=-\frac{\mathrm{dE}}{\mathrm{dr}}
\end{equation}
Now let's apply this same relationship to Coulomb's Law for the force. Rearranging gives
\begin{equation}
d E=-\mathrm{Fdr}=-\frac{\mathrm{kq}_1 \mathrm{q}_2}{\mathrm{r}^2} \mathrm{dr}
\end{equation}
Using calculus and integrating both sides of the equations gives this general relationship between E and r for the electrostatic forces:
\begin{equation}
E=\mathrm{kq}_1 \mathrm{q}_2\left(\frac{1}{\mathrm{r}}\right)
\end{equation}
A graph of Epot vs r for the electrostatic force is shown in Figure \(\PageIndex{4}\). Note that the curves are hyperbolic (1/r) functions of r. There are attractive OR repulsive components.
An equation for Epot vs r for the induced dipole-induced dipole interactions can also be derived. For this interaction, Epot has a different dependency on r and has both an attractive (Epot α -1/r6) AND repulsive term (Epot α +1/r12) which are added together. This potential is called the Lennard-Jones or 6-12 potential. Figure \(\PageIndex{5}\) shows the total and component attractive and repulsive terms Epot vs r. Note how similar these curves are to the graphs for electrostatic energy.
Now, let's look at the noncovalent interactions more carefully using examples of small and big molecules.
Ion-Ion
All introductory chemistry and biology textbooks differentiate ionic and covalent bonding. Ionic bonding occurs between fully charged species. Some ions are monatomic (like Na+ or Cl-), formed from gaining or losing electrons. Others are polyatomic (like ammonium - NH4+ or acetate - CH3COO-, generally formed from molecules gaining or losing protons in Brønsted acid/base reactions. Polyatomic ions are also called molecular ions. An example of the monatomic salt NaCl and the molecular salt ammonium acetate are shown in 2D Lewis structure and molecular modeling representations (spheres and sticks) in Figure \(\PageIndex{6}\): below.
Now, an intramolecular ionic bond can form within a larger molecule if a negatively charged group in the molecule comes close enough in 3D space to a positively charged group in the same molecule. In contrast to the examples shown above, the ionic bonds within large molecules like proteins do not occur within a large lattice of ions held together by multitudes of similar ionic bonds. Rather a single ionic bond could exist and persist in a larger molecule held together by a multitude of other noncovalent interactions. An ionic bond between a single monatomic or polyatomic cation and an anion would not exist in an aqueous solution long as the species would dissociate into separate ions solvated by water. Hence the ionic bonds that exist between charged groups within a large molecule like a protein exist in such a different environment than a solid crystal lattice that we give it a different name. It is called a salt bridge, as the ionic bond bridges distal parts of the larger molecule. We also categorize it as an ion-ion noncovalent attraction.
Figure \(\PageIndex{7}\) shows a salt bridge/ion-ion interaction (represented as a yellow line) between the side chains of two amino acids, aspartic acid (Asp) 67 (-CH2COO-, similar to acetate) and lysine (Lys) 69 (-RCH2NH3+, similar to NH4+) in a protein, human lysozyme.
Figure \(\PageIndex{8}\) shows an interactive iCn3D model of a salt bridge/ion-ion interaction between the carboxylate side chain of Asp 67 and the amine side chain of Lys 69 in human lysozyme (1REX).
Figure \(\PageIndex{8}\): Salt bridge (represented as a yellow line) between Asp 67 and Lys 69 in human lysozyme (1REX). (Copyright; author via source).
Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...1qpAtSs3CuvVs8
Most of the protein's atoms have been removed to simplify the structure. We haven't studied proteins yet, but to a first approximation, they are polymers consisting of amino acid monomers. The backbone of the polymer contains a repeating amide group which contains an N-H hydrogen bond donor and a C=O hydrogen bond acceptor. Each amino acid contains an R group side chain oriented away from the backbone. The R groups can be fully charged, polar or nonpolar.
This protein, containing 129 amino acids in a large polymer of over 1000 atoms, has just 10 salt bridges/ion-ion interactions within the most stable structure of the protein. The structure files that contain the x,y, and z coordinates of the atoms in a large biomacromolecule like a protein usually don't give coordinates for hydrogen atoms in the structure since they are too small to detect by techniques such as x-ray crystallography or cryoelectron microscopy, which are used to determine the structure of large biomacromolecules. Computer programs can be used to add them so they can be visualized in modeling programs. The left molecule in Figure 8 shows a stick model of just a small part of the protein containing a single salt bridge/ion-ion interaction. The blue represents nitrogen with a +1 formal charge in the side chain of lysine.
Hydrogen atoms have been added to the right molecule to illustrate the actual distance between adjacent atoms. Quantum calculations of actual electron density in molecular ions such as H3O+ and NH4+ (and charged amines) show that the electron density in these cations is actually shifted to the electronegative O and N atoms with electron deficiencies over the bonded H atoms (in contrast to the simpler ideal of formal charge), even though we state that the N in a charged amine has a positive formal charge.
As the distance r between interacting groups increases past the optimal interaction distance, the attractions decrease. When modeling most noncovalent interactions in large molecules, programs generally use cutoff values of 5-6 Angstroms, beyond which the interactions do not contribute to stabilization. The ion-ion interaction is the strongest interaction of all, given a fixed distance for comparison.
Hydrogen Bond (H-bond)
The name hydrogen bond is a bit ambiguous, which leads to its misunderstanding by students. It is not a covalent bond between two atoms, X and H, such as C-H and O-H in methane and water, respectively. Rather it is a noncovalent interaction between a slightly positive H on an electronegative atom X and a slightly negative electronegative atom Y on another molecule or part of a large molecule. X and Y are electronegative atoms such as F, O, or N with lone pairs The H on X-H (for example O-H or N-H) is slightly positive (δ+) since the X-H bond is polar covalent, and electron density in the bond is drawn toward the electronegative atom (for example O or N). Given its small size compared to all other atoms, a slightly positive H, can get very close to a lone pair on a slightly negative (δ-) electronegative atom Y (for example O or N) on another molecule. Since r, the distance between the δ+ H and δ- N or O on two separate molecules is small, Coulomb's Law informs us that the attractive force is significant. This interaction is highly directional and distance-dependent, which accounts for the large range in relative strength (3-15 kcal/mol, 12-63 kJ/mol) for hydrogen bonds within large molecules.
Hydrogen bonds occur between hydrogen bond donors and acceptors. This is determined by looking at the slightly negative electronegative atoms in the two interacting molecules. An alcohol (ROH) can be either a hydrogen bond donor or acceptor, while a ketone (R)C=OR) can only be an acceptor since it has no slightly positive H. In a hydrogen bond between an alcohol and a ketone, the O-H on the alcohol is the hydrogen bond donor while an O=C on the ketone is the hydrogen bond acceptor. This is illustrated in Figure \(\PageIndex{9}\) below.
Figure \(\PageIndex{9}\): A hydrogen bond between a donor and acceptor
In a given hydrogen bond, the donor is the X-H with the slightly positive H.
Figure \(\PageIndex{9}\) shows multiple representations of a central water molecule hydrogen-bonded to four other water molecules. The left image shows lone pairs as purple spheres.
A common difficulty for students is to identify which of the many hydrogen atoms in any structure can engage in hydrogen bonds. One way is to circle all δ+ Hs in structures (i.e. those covalently attached to N or O) and see if there are any nearby δ-: N or :O atoms close enough to form a hydrogen bond. Figure \(\PageIndex{10}\) shows a molecule of methanol forming two hydrogen bonds to two different water molecules. Only 1 of the 4 Hs on methanol is δ+ (circled in green). The others are bonded to the carbon through nonpolar covalent bonds.
Hydrogen bonds are abundant in large molecules like proteins. They occur between backbone atoms, between backbone and side chains atoms, between side-chain atoms, and between protein atoms and water. Their strength depends on the magnitude of δ+ and δ- charges on the H bond donor and acceptor atoms, respectively, the distance r between them, and the angle of the bond Three types of H bonds have been categorized based on their relative strengths, based in large part on the distance between the donor and acceptor:
- conventional (weakest of these 3 so sometimes called weak), 2.4 to 12 kcal/mol (10-50 kJ/mol)
- strong or low barrier, 12 to 24 kcal/mol (50-100 kJ/mol), often called short hydrogen bonds (SHB)
- very strong or no barrier >24 kcal/mol (100 kJ/mol), (Frey et al).
In large proteins of known 3D structures, H bonds are calculated by locating all donors and acceptors with 3 +/- x angstroms from each other. Most structural files do not include H atoms, so the 3 Angstrom distance is from the centers of the electronegative atoms, typically N and O, involved in the hydrogen bond, as shown in Figure \(\PageIndex{11}\) (purple bracket).
Conventional H bonds vary between 2.8-3.2 A, which gives a distance range from the actual δ+ hydrogen on the donor to the acceptor δ- N or O (the red line below) of 1.8 to 2.2 A. Short H bonds are < 2.7A which is smaller than the sums of the van der Waals radii of N and O (blue and red circle below), suggesting that the bond has a covalent character (see below). Those between 2.5 - 2.7 are characterized as strong, low barrier, or short hydrogen bonds. Analysis of a large number of PDB structures of proteins shows many short hydrogen bonds characterized by these properties:
- the donor and acceptor electronegative atoms A and B are N or O
- r, the separation distance, is 2.3 A to 2.7 °A
- the A–H–B angle is 1350.
Detailed analyses of high-quality protein structures show one short hydrogen bond for every 16 conventional ones. They are found in proteins, protein-ligand complexes and in DNA. They are involved in many aspects of molecular function.
It would seem likely that the δ+ H atom, which is covalently attached to a heteroatom like O or N (A), and which is attracted to another heteroatom B, could be exchanged between the two heteroatoms as shown in the chemical equation below, where ---- represents an H bond.
A-H ----B ↔ A ----H-B
A very strong/no barrier H bond occurs if A and B are very close, have similar δ- charges, and have similar pKa so that the H atom could be equally shared between A and B. It is represented by the representation below.
A ||| H ||| B
An example is FHF- (F||| H |||F)- in which there is no barrier for the H to move from one heteroatom to another.
It thus appears that for strong and very strong H bonds, what we call the hydrogen bond has some covalent bond character. Quantum calculations show an overlap between the unoccupied antibonding σ*molecular orbital of X-H (the hydrogen donor) and the non-bonding lone electron pair molecular orbital of the hydrogen bond acceptor molecule.
Even though water is a simple and ubiquitous molecule, scientists still struggle to understand its properties. Lewis structures of water can explain only so much of its physical and chemical properties. However, look at Figure \(\PageIndex{12}\), which shows the electron density around water calculated using quantum theory.
Do you see any "rabbit ears" (i.e. lone pairs) emanating from the oxygen atom? Don't think so! Nevertheless, everyone still uses Lewis structures with lone pairs to explain the chemistry of water and other molecules. We present this figure, in advance of a discussion at the end of this section on the halogen bond, which requires an understanding of electron density around bonded atoms.
Now let's look at some hydrogen bonds within a single protein molecule. Figure \(\PageIndex{13}\) hydrogen bonds (yellow dotted line) between serine (Ser) 24 (side chain -CH2OH) and asparagine (Asn) 27 (side chain -CH2(C=O)NH2 of hen egg white lysozome (1REX). As in the figures above showing salt bridges, two images are shown, one with polar H atoms added. Find the hydrogen bonds between side chains, side chains and backbone, and between backbone hydrogen bond donors and acceptors.
Proteopedia has an excellent review of hydrogen bonds.
Dipole-Dipole
This interaction involves the alignment of permanent dipoles in molecules such that the geometric center of the δ+ of one permanent dipole on one molecule is close to and aligned with the geometric center of δ- of the permanent dipole on another. Figure \(\PageIndex{14}\) shows two acetone molecules interacting through dipole-dipole interactions. These molecules can't form hydrogen bonds to each other since they both contain just hydrogen bond acceptors.
The arrow represents the molecule dipole moment vector (as opposed to individual bond dipole moment for each polar covalent bond in the molecule). Note the difference in Figure \(\PageIndex{15}\). The molecular dipole is the vector sum of the bond dipoles.
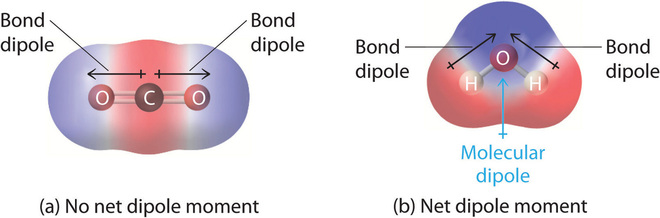
None of the H atoms bonded to carbon in acetone are δ+ so the molecules contain no H bond donors. Although they contain a δ- oxygen, a hydrogen bond acceptor, two molecules of acetone cannot hydrogen bond to themselves. They can form hydrogen bonds to water. Pure liquid acetone evaporates readily (BP 560 C) due to this lack of strong hydrogen bonds.
You can imagine two water molecules forming dipole-dipole interactions as well. However tilting the molecule to align the lone pair on an O with the δ+H on another water molecule and presto, you have a hydrogen bond. H bonds are often viewed as a special case of a dipole-dipole interaction.
Modeling programs can determine the charge on each atom of a large molecule like a protein and determine the geometric center and magnitude of overall + and - charge. A line drawn between them represents the permanent "dipole" moment of the entire protein. More simply, the molecular dipole is the vector sum of all of the individual bond dipole moments. Entire proteins have a net dipole moment which probably facilitates the interaction of the protein with other proteins or ligands. Figure \(\PageIndex{16}\) shows the net dipole moment for the protein carboxypeptidase A1 (2v77). This was calculated using the Protein Dipole Moments Server. Proteins, however, do have net charges (not considering any bound counterions) so the molecular dipole for a protein is a bit different conceptually than for a small molecule. Nevertheless, it is a good way to quantitate asymmetric charge distribution in large biomolecules. Asymmetric charge distributions would influence molecular properties.
Ion-Dipole
Figure \(\PageIndex{17}\) shows interactions between a Na+ ion and the dipoles of multiple water molecules.

Figure \(\PageIndex{18}\) shows an interactive iCn3D model of the molecular ion sulfate SO42- bound to a protein through its hydrogen bonding and ion-dipole noncovalent interactions with protein side chain and backbone groups in the sulfate binding protein from Salmonella typhimurium.
.png?revision=1&size=bestfit&width=311&height=246)
The SO42- is buried within the protein. The green and yellow dotted line show hydrogen bonds between the sulfate and amide N-Hs on the protein chain surrounding it and the a side chain of the protein. Modeling programs don't show lines depicting dipole-x interactions. The SO42-, through its oxygen, can form hydrogen bonds with nearby donors.
Figure \(\PageIndex{19}\) shows an interactive iCn3D model of another example of a protein backbone and side chains ion-dipole interactions, this time with a Na+ ion, a simple non-transition state metal ion, which can not form hydrogen bonds. The protein is tryptophan synthase from Salmonella typhimurium (6dz4). The red spheres represent water oxygen atoms (no hydrogen atoms shown).
.png?revision=1&size=bestfit&width=379&height=241)
The ions illustrated in these last two cases are not transition metal ions, whose interactions with ligands can best be considered using ligand field theory and the formation of covalent (dative) bonds between electron pair donors on nucleophilic side chain/main chain atoms and d orbitals on the transition metal.
Induced Dipole - Induced Dipole/Hydrophobic Interactions.
These noncovalent interactions occur when a temporary dipole, created by random fluctuations in electron density in one molecule, induces a temporary dipole in another molecule nearby. These interactions are weak and can easily be broken by raising the temperature. Induced dipole-induced dipole interactions allow nonpolar gases like He, N2, O2, and CH4 to be liquefied, but it takes higher pressures and/or low temperatures to force the molecules close enough and slow them down enough for sufficient interactions to occur to liquefy the molecules. Although individually weak, the larger the molecules, the greater the extent of induced dipole-induced dipole interactions and the stronger the interactions among molecules. This is reflected in the fact that methane, CH4, is a gas at room temperature, octane, C8H18 is a liquid and C30H62 is a solid.
Figure \(\PageIndex{20}\) shows induced dipole interactions between two molecules.
Induced dipole-induced dipole interactions are important among large biomolecules as well. Most biologists and probably biochemists prefer to use the words hydrophobic interactions (but not hydrophobic forces) instead of the longer and more formal induced dipole-induced dipole interaction. We will also try to use the more commonly used term within the biochemistry community.
Figure \(\PageIndex{21}\) shows an interactive iCn3D model of a hydrophobic cluster around the side chain of a hydrophobic amino acid, valine 143 in human carbonic anhydrase II (4ca2). Val 143 is highlighted in yellow and shown with normal atom (CPK) colors. White to green indicate nonpolar amino acids while dark blue indicates polar ones.
.png?revision=1&size=bestfit&width=314&height=270)
You can see that the side chain of Val 143 (highlighted in yellow) is completely surrounded by nonpolar amino acids. If the structure was rendered in spacefill instead of sticks, Val 143 would be closely packed to maximize induced dipole-induced dipole (hydrophobic)interactions.
Induced dipole-induced dipole interactions also occur between polar molecules, but they are weaker than the hydrogen bonding and dipole-dipole interactions between them.
Pi stacking
Aromatic rings stacked over each other can interact through induced-induced dipole (hydrophobic) and dipole-induced dipole interactions. These interactions can depend on the presence of heteroatoms in the aromatic ring. Figure \(\PageIndex{22}\) shows an example with benzene in which a staggered arrangement of the rings is more attractive.
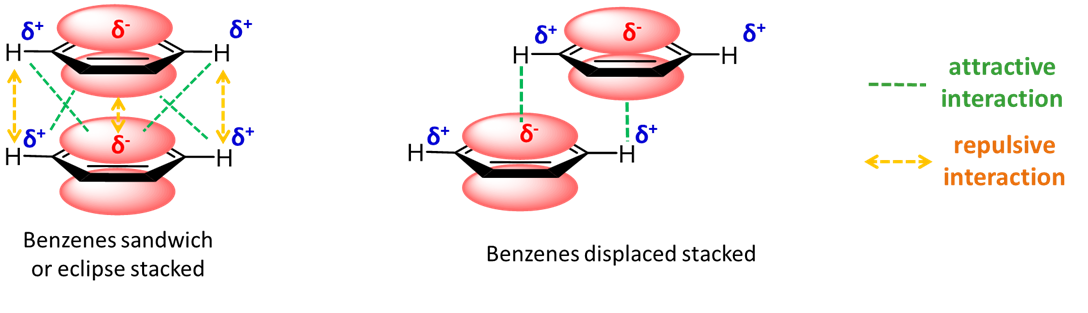
For a biological example, everyone is familiar with the structure of B-DNA in which the bases A, G, C and T point inward perpendicular to the double helix axis and are stacked over each other.
Figure \(\PageIndex{23}\) shows an interactive iCn3D model of a short stretch of DNA with a sugar-phosphate backbone and bases colored in magenta and cyan. Fives bases on one strand are shown in stick and atomic color to show the pi-stacking interactions of the aromatic ring.
.png?revision=1&size=bestfit&width=378&height=200)
Pi stacking also occurs in proteins. Figure \(\PageIndex{24}\) shows an interactive iCn3D model of two sets of pi stacking interactions in the protein arginine kinase (1M15). The aromatic side chains involved in pi stacking are shown in cyan.
.png?revision=1&size=bestfit&width=289&height=282)
Cation - Pi
Figure \(\PageIndex{25}\) shows an interactive iCn3D model a specific example of an ion-induced dipole interaction (called a cation-pi interaction) between a sodium ion (blue sphere) and the aromatic ring of the side chain tryptophan (cyan) in hen egg white lysozyme (1lpi).
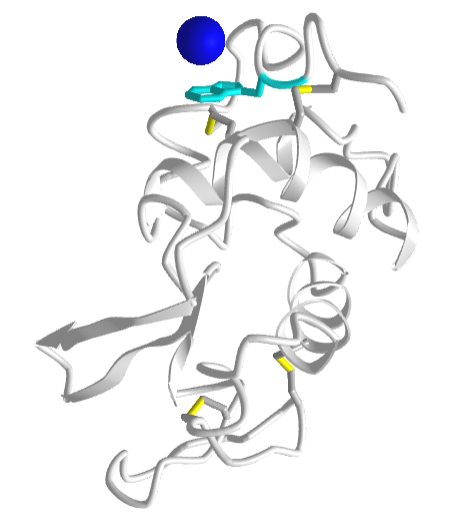
For another example of a cation-pi interaction, open up iCn3D with 1REX and view the interaction of lysine (K1) side chain with the nonpolar aromatic ring of phenylalanine (F3).
Solution
Here are some more examples.
Exercise \(\PageIndex{1}\)
Select the link below to answer the following questions.
1. What type of noncovalent interaction best describes the red dotted line in the structure?
2. What type of noncovalent interaction best describes the red dotted line in the structure?
- Answer
-
1. cation-pi
2. pi stacking
Halogen Bond
Lastly, we come to the halogen bond. You might ask if there are halogens found in proteins. The answer is no (until one is found!) but halogenated molecules (drugs, xenobiotics, toxins) bind proteins. Consider the C-X bond where X is a halogen. The electronegativity of C is 2.56 while the halogens have these electronegativity values: F (3.98), Cl (3.16), Br (2.96), and I (2.66). Compare these to oxygen (3.44) and N (3.04). Covalent bonds between two bonded atoms whose electronegativity differences are between 0.4 and 1.8 are considered polar covalent, so C-F, C-Cl, and C-Br are considered polar covalent. The C-I bond is the longest and iodine is the most polarizable of these halogens. An alkyl halide with a C-I bond can undergo SN2 nucleophilic substitution reactions with I- being an excellent leaving group. Hence the C-I bond behaves somewhat as a polar covalent bond.
Nevertheless, quantum calculations show that the electron density is not uniformly spread around the X halogen in a C-X bond, but rather is pulled more toward the C, leaving the distal end of the halogen depleted in electron density and slightly positive. This region of relatively depleted electron density is called the σ-hole. Color-coded renderings of the electron density of the halogen involved in a C-X bond show the halogen atom to have bands (like Jupiter) with the more negative electrostatic potential (represented in blue) closest to C and the more positive potential, the σ-hole (represented in red), at the end farthest from the C atom. Calculations show that this effect is greatest for the heavier halogens (Br, I) which have longer C-X bonds. The halogen's slightly positive σ-hole can act analogously to a hydrogen bond donor in its interactions with nearby δ- :O and :N atoms/lone pairs. This might take a while to grasp. You have always heard that in general the halogens are more electronegative than carbon and would hence always be δ- when bonded to it. This case is similar to our chemical intuition about lone pair "rabbit ears" on oxygen, which quantum calculations show not to be an accurate representation of the electron density (see Fig xx).
Figure \(\PageIndex{26}\) shows the electrostatic potential on a halogen X atom covalently attached to a carbon in two different molecules, CF3-I and :NC-Br. The red distal end is the σ-hole relatively depleted in electron density and with a higher, more positive electrostatic potential. (This is opposite the usual coloration that biochemists use in which oxygen (δ- or fully -) is colored red and nitrogen (in a protonated amine with a positive charge) is shown in blue.)
Figure \(\PageIndex{27}\) shows a molecule with a carbonyl (a hydrogen bond acceptor with a δ- :O) interacting with another molecule through either a hydrogen bond or a halogen bond. Again the red distal end of the halogen X is the σ-hole relatively depleted in electron density.
Medicinal chemists use halogen substituents on drug molecules to alter drug binding specificity, membrane diffusion, and t1/2. Increasingly, they are using halogen bonds in rational drug design to increase drug affinity to target proteins.
Figure \(\PageIndex{28}\) shows an interactive iCn3D model below shows the interaction of a haloaminopyrimidine inhibitor bound to its binding site on the c-Jun N-Terminal Kinase (JNK) protein (2P33).
_protein_(2P33).png?revision=1&size=bestfit&width=301&height=260)
Note that the sulfur of methionine is forming a halogen bond with the Cl atom. Although the electronegativity of sulfur is 2.58, close to that of carbon (2.55), nevertheless, sulfur is larger and more polarizable so it also develops a slightly positive σ-hole distal to the carbon atom. Analysis of PDB files shows that S--O interactions are common in proteins and most likely impact protein stability.
Ultimately all ensembles of molecules/ions reach a low if not the lowest energy state under a given set of conditions. Noncovalent attractions are maximized and repulsions are minimized to achieve this state. Consider for example solid sodium chloride held together by ionic bonds. The ions are closest packed (face-centered cubic) and cannot get closer together (packing density of about 74%) as simple packing considerations and repulsive electrostatic forces and collective van der Waals interactions would prevent it. Each Na+ is surrounded by 6 Cl- ions and vice versa.
When large molecules like proteins assume a low energy state, they maximize the attractive noncovalent interactions described in this section while minimizing repulsive ones within a molecule (in given solvent conditions). Packing density reaches similar values as for closest packed spheres (NaCl for example). Figure \(\PageIndex{29}\) shows a slice through a protein and through the crystal lattice of NaCl. The gray circles on the protein show the faces of the sliced atoms. They are superimposed on the surface of the protein shown in colored spheres. If you took a series of cross-sectional slices throughout the protein, you would get a better picture of packing density than a single slice alone. Collective van der Waals interactions are found among all atoms and ions in a protein, which accounts for the closest packing of most atoms, polar and nonpolar, with the packed protein structure.
Here is a link to a JSmol tutorial by David Marcy et al, An Introduction to Chemical Bonds and Protein Structure
Summary of Noncovalent Interactions in Biomolecules
It is not easy to understand noncovalent interactions among small molecules let alone within solvated and densely packed proteins, for example. To help quantitate strong noncovalent interactions involving amino acid side chains, Xie et al have studied amino acids in the gaseous phase using quantum mechanics. Here are some general conclusions (Xie et al. PLoS ONE 10(9): e0137113. https://doi.org/10.1371/journal.pone.0137113. Creative Commons Attribution License)
- Ion-Ion (salt bridge) interactions between acidic amino acids side chains (Glu- and Asp-) and alkaline amino acids side chains (Arg+, Lys+ and His+) are the strongest residue-residue interactions. However, this type of interaction may be weakened by solvation effects and broken by lower pH conditions.
- Cation- interactions between protonated amino acid side chains (Arg+, Lys+ and His+) and aromatic amino acid side chains (Phe, Tyr, Trp and His) are 2.5 to 5-fold stronger than common hydrogen bond interactions and are less affected by the solvation environment.
- Amide bridge interactions, shown in Figure \(\PageIndex{30}\) below, which contain two hydrogen bonds, between the two amide-containing amino acid side chains (in the amino acids Asn and Gln) are three times stronger than hydrogen bond interactions, which are less influenced by the pH of the solution.
Figure \(\PageIndex{30}\): An "amide" bridge (Xie et al, ibid)
- Ten of the twenty natural amino acids are involved in salt bridge, cation, or amide bridge interactions that often play important roles in protein-protein, protein-peptide, protein-ligand, and protein-DNA interactions.
Secondary Forces in Protein Structure and Function
Recent Updates (01/7/04). Another computational study was done to categorize the noncovalent interactions between proteins and small molecules (drugs, inhibitors) that bind to them. These small molecules are generically called ligands, a term used in the study of transition metal complexes. They studied 11,016 unique structures found in the Protein Data Bank of small-molecule ligands bound to proteins. A histogram displaying the number of each type of interaction between small ligands and proteins is shown in Figure \(\PageIndex{31}\) below.
Figure \(\PageIndex{31}\): Frequency distribution of the most common non-covalent interactions observed in protein–ligands extracted from the PDB. de Freitas and Schapira. Med. Chem. Commun., 2017, 8, 1970-1981. de Freitas and Schapira. DOI: 10.1039/C7MD00381A (Research Article)
Two new interactions are shown, the weak or better called nontraditional hydrogen bond and amide stacking. Amide stacking is readily understandable as an interaction between the slight positive carbonyl carbon of the amide and the electron-dense pi cloud of the aromatic ring. They are part of a group of interactions that are based on "secondary forces" between a ligand and protein, and within proteins and also carbohydrates, which we will explore in a future chapter. They include main chain interactions (nontraditional H bond, calchogen bonds and n→π*) and interactions with aromatic side chains. These secondary "forces" are shown in Figure \(\PageIndex{32}\) below.
Figure \(\PageIndex{32}\): Secondary Interactions in protein (adapted from Newberry and Raines, ACS Chem. Biol. 2019, 14, 8, 1677–1686.
You probably find the nontraditional hydrogen bond more troubling. The hydrogen bond donor is a carbon atom attached to a hydrogen, and a hydrogen bond acceptor, the carbonyl oxygen. We have stated that a C-H bond does not engage in a hydrogen bond. We assumed that a C-H bond is sufficiently nonpolar so the carbon atom does not have a slight negative charge which leaves hydrogen without a slight positive. Yet it appears that there are many C–H⋯O weak hydrogen bonds between ligands and proteins and also within proteins.
C has an electronegativity of 2.5 and H 2.2 with a difference of 0.3, which is a much smaller difference than between N and H (3.04-2.2 =0.8). If the electronic environment around the carbon enhances its slight negative charge, then you could imagine that a C-H could be a hydrogen bond donor. The median distance of the C–H⋯O nontraditional hydrogen bond was 3.4 Å, which is 0.4 Å longer than traditional hydrogen bonds (N–H⋯O, N–H⋯N, O–H⋯O), with an angle of around 130° (compared to an optimal of 109.50. The Cα–H⋯O=C interactions are about one-half the strength of an NH⋯O=C hydrogen bond. Hence they are weak. In the rest of this book, we will rarely see a nontraditional C-H bond as a candidate for a hydrogen bond. Nevertheless, it is important to mention it given their prevalence.
The other main chain interactions, n → π*, might look like a dipole-dipole interaction. It has its roots in the molecular (not atomic) orbitals for carbonyls in the backbone. Simple molecular orbital (MO) theory predicts the general energy levels for the molecular orbitals. The binding orbitals (σ for the sigma bond and π for the pi bond are filled with electron pairs and stabilize the molecule. The nonbonding electrons in the carbonyl O are in nonbonding orbitals n (neither stabilizing nor destabilizing). The antibonding σ* and π* orbitals on the adjacent carbonyl are unfilled and are higher in energy. (Remember that if you bring two atomic orbitals (like 1s and 1s from 2 hydrogen atoms) to form an energy-stabilized covalent bond, you get 2 MOs (σ and σ*). The relative energy of these MOs for carbonyl are shown below in Figure \(\PageIndex{33}\):
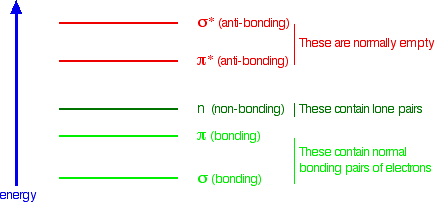
Figure \(\PageIndex{33}\): Relative energy levels of molecular orbitals (not to scale). https://chem.libretexts.org/Bookshel...c_Spectroscopy
The interaction must involve some stabilizing electron donation from the n orbital to the π* orbital.
Figure 33 shows some aromatic interactions that occur from the side and not the top of the plane of the ring. These are understandable if you consider the 3D electrostatic potential map of benzene, as shown in Figure \(\PageIndex{34}\) below.
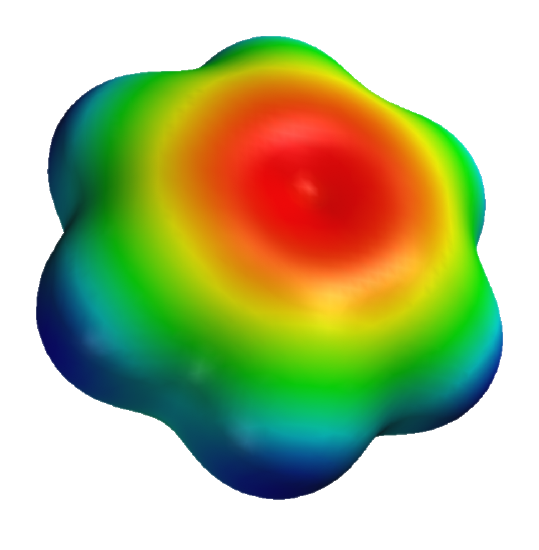
Figure \(\PageIndex{34}\): 3D electrostatic potential of benzene. https://en.wikipedia.org/wiki/File:B...-potential.png
Note that the sides are bluish which represents more positive electrostatic potential which would lead to the attraction of anion or S atoms with high electron density.
References
IUPAC. Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997). Online version (2019-) created by S. J. Chalk. ISBN 0-9678550-9-8. https://doi.org/10.1351/goldbook.
https://chem.libretexts.org/Bookshel...g_interactions
https://boisestate.pressbooks.pub/ch...ecular-forces/
A low-barrier hydrogen bond in the catalytic triad of serine proteases, PA Frey et al, Science 264, 1927-1930 (1994)
DOI: 10.1126/science.7661899




.png?revision=1&size=bestfit&width=359&height=289)