11.2: Diffusion Across a Membrane - Passive and Facilitated Diffusion
- Page ID
- 14985
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Understand the structure and function of biological membranes.
- Describe the different types of diffusion and how they operate across a membrane.
- Explain the concept of concentration gradient and how it drives diffusion.
- Describe the mechanisms of passive and facilitated diffusion, including their differences and similarities.
- Understand the role of carrier proteins and channels in facilitated diffusion.
- Describe the factors that can affect the rate of diffusion across a membrane.
- Understand the importance of membrane transport in maintaining homeostasis in cells and organisms.
Diffusion Across a Membrane
We have studied molecular aggregates (micelles and bilayers) and macromolecular structures (mostly proteins). We also studied binding interactions which are the first steps in the expression of the biological activity of a macromolecule. For some proteins, reversible binding is their sole function (consider the binding of dioxygen to myoglobin and hemoglobin). For many others, it is not. For those, what can happen next?
You already have one possible answer. A bound reactant, which we will call a substrate, can be converted to a product in a chemical step involving the breaking and making of covalent bonds catalyzed by a protein enzyme. However, there is an even simpler process that does not involve covalent bond changes. If a small molecule is bound to a membrane protein, it could be transported in a purely physical step across a membrane. Just as reactions can proceed with and without an enzyme, a solute can move down a concentration gradient across a semi-permeable membrane, driven by diffusion alone in a thermodynamically favorable process, either by itself, in a process called passive diffusion, or with the assistance of a membrane protein, in a process called facilitated diffusion. Large pores made of assemblies of proteins can also be formed that allow the passage of many solutes across the membrane.
There are many occasions when it would be optimal to move a molecule across a membrane from a region of low to high concentration. This process is called active transport. It is not thermodynamically favored so it requires an external energy source. This is often the thermodynamically favored cleavage of ATP to ADP and Pi. The uphill transport can also be powered by the downhill diffusion of a "co-transport" molecule from high to low concentration. We will explore all of these processes in this and the remaining chapter sections. First, we should understand the simplest process, "passive diffusion", that requires no protein "help".
Let's step back and think about how difficult it is for a chemical species to cross a lipid bilayer. Chemical intuition would tell us that both size and polarity are important. The bigger the size and the greater the charge, the more difficult it would be to cross the membrane. The permeability coefficient is related to the ease with which solutes traverse the membrane. Figure \(\PageIndex{1}\) shows the permeability coefficients for relevant biological molecules.
Smaller, higher charge density ions (like Na+) have a lower permeability coefficient than do larger, lower charge density ions (like K+) as seen in (Table \(\PageIndex{1}\)). What about natural membranes?
| Membrane Preparation | D-Glucose | D-Mannitol |
|---|---|---|
| Synthetic Lipid Bilayer | 2.4 x 10-10 | 4.4 x 10-11 |
| Calculated Passive Diffusion | 4 x 10-9 | 3 x 10-9 |
| Intact Human Erythrocyte (red blood cell) | 2.0 x 10-4 | 5 x 10-9 |
Looks like D-glucose gets a little help in getting across. We'll see the mechanism below.
Passive Diffusion
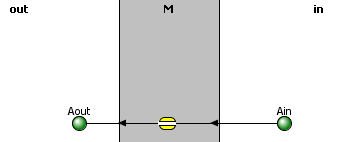
Let's start with the passive diffusion of uncharged solute A across a membrane, which can be represented by the chemical equation Aout ↔ Ain. Intuitively, you probably believe that the rate of net diffusion or the flux of A across the membrane is directly proportional to the concentration gradient across the membrane. If concentrations of A are identical across the membrane, the net flux J should be 0. If you double the concentration gradient, the net rate should double. We will see that the net rate is a linear function of [ΔA] across the membrane. Figure \(\PageIndex{2}\) shows the flux of Aout across a semipermeable membrane of thickness Δx (we will use dx instead when Δx is very small).
Let's animate diffusion using a PHET simulation, as shown in Figure \(\PageIndex{3}\).
Figure \(\PageIndex{3}\): PHET animation of passive diffusion. PHET: https://phet.colorado.edu/
The flux of molecules \(A\) (\(J_A\)) is proportional to the concentration gradient across the membrane, \(ΔA/Δx\) (which we will refer to as \(dA/dx\) which is the derivative of \(A\) with respect to \(x\)). The equation below is Fick's First Law of Diffusion:
\[\mathrm{J}_{\mathrm{A}} \propto \frac{d \mathrm{~A}}{d x}=-\mathrm{D} \frac{d \mathrm{~A}}{d x} \label{Ficks1}\]
where \(D\) is the diffusion coefficient. The negative sign is necessary since concentration increases to the left in the figure above in the opposite direction of net flux which is to the right. For these derivations, we will assume the JA is the initial flux. That is, the flux is measured for a short enough time that the relative concentrations of A on both sides of the membrane do not change significantly. It should be clear that eventually the net flux levels off to zero when the concentrations of A on both sides of the membrane are equal. Under these conditions, the free energy \(G_{A\, out}\) = \(G_{A\, in}\), so \(ΔG = 0\). This thermodynamic relation can also be expressed as
\begin{equation}
J_A=-L \frac{d G_A}{d x}
\end{equation}
This equation bridges the kinetic and thermodynamic aspects of diffusion.
Dimensional analysis of Fick's 1st Law (Equation \ref{Ficks1}) shows that the units of \(D\) are cm2/s which gives the number (dimensionless) of molecules crossing a 1 cm2 surface area of membrane each second.
\(J\) = moles/area/sec = mol/cm2.s = - (cm2/s) mol/cm3/cm. Hence the units of \(D\) are cm2/s.
Let's rearrange Fick's 1st Law and use a bit of calculus to get Equation 4.
\begin{equation}
\begin{gathered}
\mathrm{J}_{\mathrm{A}} \int_0^{\mathrm{x}} \mathrm{dx}=-D \int_{\mathrm{A}_{\text {out }}}^{A_{\mathrm{in}}} \mathrm{dA} \\
\mathrm{J}_{\mathrm{A}} \mathrm{x}=-\mathrm{D}\left(\mathrm{A}_{\mathrm{in}}-\mathrm{A}_{\mathrm{out}}\right) \\
\mathrm{J}_{\mathrm{A}}=\frac{\mathrm{D}}{\mathrm{x}}\left(\mathrm{A}_{\text {out }}-\mathrm{A}_{\mathrm{in}}\right)
\end{gathered}
\end{equation}
or
\begin{equation}
J_A=P\left(A_{\text {out }}-A_{\mathrm{in}}\right)=P \Delta A
\end{equation}
where P is the permeability coefficient, which has units of cm2/s/cm or cm/s. (We discussed permeability coefficients for different solutes traversing model bilayers when we discussed lipids.) That unit is less intuitive to understand but the final unit is very intuitive.
A plot of JA vs (Aout - Ain) is linear, with a slope of P = D/x
It's important to remember that there is still diffusion of A across the membrane at equilibrium since the equilibrium is dynamic. There is no net diffusion, however. This is where animations come in handy.
The table below shows the reaction diagram (left), graphical results of the progress curve(middle), and animations for the reversible diffusion Aout ↔ Ain across a membrane with the conditions shown below. The reactant A and product are called species and are shown as green spheres. The yellow square is a reaction node indicating a reaction connects A to P. The lines connect the species that participate in the reaction. The velocities (slope of the concentration vs time curve at any given time) are called fluxes, J, in Vcell and many other similar programs. When we get to metabolism, we will talk about fluxes of metabolites through pathways. Also, fluxes are used to describe the rate of movement of solute through membranes.
Animations
Now let's look at animations of the same passive diffusion reaction of a neutral species across a semi-permeable membrane. Animations are by Shraddha Nakak and Hui Liu.
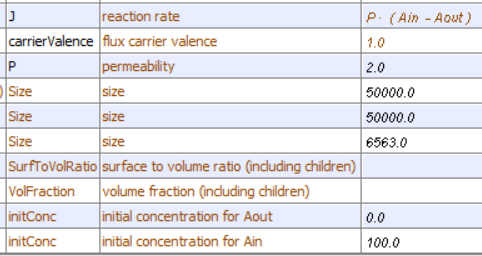
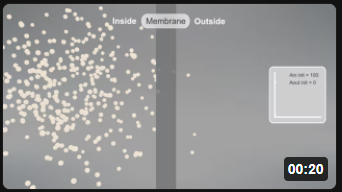
| Aout ↔ Ain [Ain]t=0 = 100; [Aout]t=0 = 0; P = 2 | Aout ↔ Ain [Ain]t=0 = 50; [Aout]t=0 = 0; P = 2 |
 |
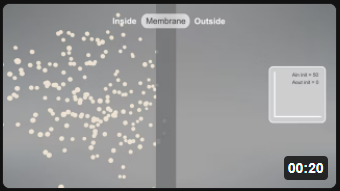 |
Note the dynamic nature of the diffusion. An equilibrium is reached when the number of particles inside equals those outside. Diffusion occurs in both directions from compartments of equal volume so that the particles moving to the outside don't escape into a comparatively huge volume. (Animations by Shraddha Nayak and Hui Lui)
Passive Diffusion of ions across a membrane - Transmembrane Potentials
Before we move on to facilitated diffusion, let's alter the scenario a bit and use a charged solute. In the example of passive diffusion above, the only thermodynamic driving force for the movement of A across the membrane was the ΔGA, the change in free energy/mol of A across the membrane (or more strictly Δμ = change in chemical potential). Solute A moves spontaneously across the membrane from high to low concentration. But what if A was charged?
We could add a bunch of positively or negatively charged species to Figure \(\PageIndex{2}\) and ask what would happen. You can't go to a chemical stockroom and find a bottle of K+ ions but you could find a bottle of neutral KCl. Let's make our experiment system a vesicle that has 0.1 M KCl in the aqueous inner compartment with 0.1 M NaCl on the outside. We could easily prepare such vesicles by making large unilamellar vesicles (LUVs) with entrapped 0.1M KCl in a solution of 0.1 M KCl and then separate the vesicles from the 0.1 M KCl not encapsulated on liposome formation using a size exclusion gel chromatography column equilibrated and eluted in 0.1 M NaCl. These vesicles are illustrated on the left of Figure \(\PageIndex{4}\).
In these prepared vesicles is there a net thermodynamic driving for K+ and Cl- to move from inside to outside the vesicle? Not for Cl- since its concentration is the same on both sides of the membrane (see Fick's 1st Law above). However, there is a clear thermodynamic driving force to take K+in → K+out. If the membrane was impermeable, net outward flux would not occur even though it is favored thermodynamically. Think of this as an example of a reaction under complete kinetic control! Note that in this example there is also a net driving force to move Na+ ion from outside to inside as well.
In our next step, let's make the membrane permeable to only K+ ions. We can do this by adding a small antibiotic, valinomycin, which binds in the membrane and once there binds and carries K+ ions across the membrane. It is called an ionophore. Figure \(\PageIndex{5}\) shows an interactive iCn3D model of K+ bound to Valinomycin.
Valinomycin, from Streptomyces fulvissimus, is a cyclic peptide consisting of L and D-Val along with L-lactate and D-hydroxyisovalerate, connected through both ester and amide bonds. The K+ ion is in the center. The six valine carbonyl oxygens bind the K+ ion. The hydrophilic groups are pointed toward the center, while the hydrophobic groups point to the outside of the structure, allowing the K+ ion to be sequestered in a polar environment as the nonpolar exterior of the complex passes through the membrane. This ionophore is specific for K+ and binds the smaller Na+ ion weakly. This can be accounted for by two factors. The smaller sodium ion doesn't bind as tightly to the chelating carbonyl oxygens. Also, the sodium ion has a higher charge density, so the Na+/water interactions must be more stable and more difficult to break than those to K+. The ion must be desolvated before it binds to the complex. Other ionophores are specific for other ions.
Once the ionophore is bound, the kinetic barriers to K+ efflux are removed and it starts moving K+ from inside to outside. However, as soon as it does, the charge balance across the membrane is lost, with the outside becoming net positive and the inside becoming net negative. A transmembrane electric potential develops across the membrane. This disfavors stops K+ efflux to the outside and eventually stops it even as the concentration difference of K+ across the membrane still favors efflux.
If you were a positive ion stuck in the middle of a membrane, as illustrated in Figure \(\PageIndex{6}\), which way would you move?
There are now two thermodynamic driving forces for K+ movement from inside to outside:
- a ΔGconcentration which favors K+ efflux. At time t=0, ΔGconcentration << 0 and it becomes a bit less negative (less favored) with efflux.
- a ΔGmembrane pot which is zero to start and slowly becomes positive, increasingly disfavoring K+ efflux.
When these driving forces are equal and opposite, net K+ movement across the membrane stops and the system is in dynamic equilbrium.
Since we use electric potential to describe electrical phenomena (electron, ion movement), we often use the word chemical potential in this case to describe the movement of ions across a concentration gradient. Add them together and we call it the electrochemical potential.
\begin{equation}
\begin{array}{c}
\Delta \mathrm{G}_{\text {electrochemical }}=\Delta \mathrm{G}_{\text {chemical }}+\Delta \mathrm{G}_{\text {electrical }} \text { or } \\
\Delta \mu_{\text {electrochemical }}=\Delta \mu_{\text {chemical }}+\Delta \mu_{\text {electrical }}
\end{array}
\end{equation}
We can use this understanding to derive an equation for flux J of a charged solute across a membrane of a given potential. The equation is called the Goldman Equation and is shown below.
\begin{equation}
J=\frac{P \frac{Z F}{R T}\left(E_{1}-E_{2}\right) C_{1}\left(1-\frac{C_{2}}{C_{1}} e^{\frac{Z F}{R T}\left(E_{2}-E_{1}\right)}\right)}{1-e^{\frac{Z F}{R T}\left(E_{2}-E_{1}\right)}}
\end{equation}
where
- P is the permeability coefficient
- Z is the charge or valence on the ion
- F is the Faraday constant
- R is the ideal gas constant
- T is temperature
- E2-E1 and the reverse is the transmembrane potential
- C2-C1 are the concentrations of the ions across the membrane
Compare this to the Nernst equation which you learned in introductory chemistry courses.
\begin{equation}
E=E^{o}-\frac{R T}{n F} \ln Q
\end{equation}
that relates the reduction potential of an electrochemical reaction to the standard electrode potential, temperature, and concentration where E is the potential difference.
Now let's run a Vcell simulation for the diffusion of an anion across a semipermeable membrane. To do so we must first set the initial transmembrane potential to solve the Goldman equation numerically. At present, this type of simulation can not be embedded into this book. So instead, the concentration vs time graphs for two different simulations, one at an initial transmembrane potential (E2-E1) = - 0.001 (i.e. 0) and one at -60 mV (a typical cell resting potential), are presented in the Figure below. In each, the reaction is A-in↔ A-out [A-in]t=0 = 100.
| A-in↔ A-out [A-in]t=0 = 100; [A-in]t=0 = 0; P = 100; Vinitial = 0 (-0.001 V) | A-in↔ A-out [A-in]t=0 = 100; [A-in]t=0 = 0; P = 100; Vinitial = -60 mV |
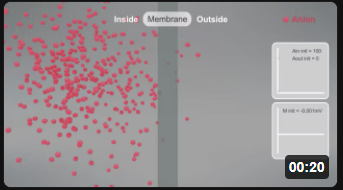
Here are animations that show the selective reversible movent of anions (A-, left panel, red) and cations (C+, right panel, cyan) as they move across a membrane from the inside to the outside. This is a very simplified simulation as it shows no counter ions on either side. Assume they exist as it would be impossible to have a "container" with just anions or cations. The initial transmembrane potential (t=0) is 0 (actually -0.001 to allow the calculations using Vcell).
| A-in ↔ A-out [A-in]t=0 = 100; [A-out]t=0 = 0; P = 100; Vinitial = 0 (-0.001 V) | C+in ↔ C+out [C+in]t=0 = 100; [C+out]t=0 = 0; P = 100; Vinitial = 0 (-0.001 V) |
 |
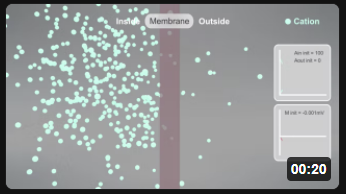 |
As anions move to the outside (left animation), the inside becomes less negative with respect to the outside, so the membrane potential V becomes more positive. This is indicated by the membrane changing to a blue color. Conversely, as cations move to the outside (right animation), the inside would become more negative with respect to the outside, so the membrane potential V becomes more negative. This is indicated by the membrane changing to a red color. (Animations by Shraddha Nayak and Hui Lui)
Facilitated Diffusion
Now let's return to the diffusion of a noncharged solute down a concentration gradient (i.e. favored) after binding to a membrane receptor. The answer to that question depends on the biological function of the macromolecule. We can simplify this process by adding one additional step as reflected in the equilibrium binding expression shown below:
\[\ce{M + L <=> ML <=> M + X} \nonumber \]
This expression indicates that the free ligand has changed in some fashion to x. In the next two chapters, we will consider two kinds of transformations:
- L is a ligand on the outside of a biological membrane (Lout) that binds to a membrane protein receptor, R. This undergoes a conformational change (as we studied in the binding of dioxygen to hemoglobin) which leads to the expulsion of the bound ligand to the inside of the membrane (Lin). This can be modeled with the simple equation:
\[\ce{R + L_{out} <=> RL <=> R + L_{in}}. \nonumber \] This process is called facilitated diffusion and represents a physical as opposed to chemical process since no covalent bonds are made or broken. This process proceeds down a concentration or chemical potential gradient (Δμ < 0) and hence is spontaneous (thermodynamically favored). If the ligand concentration is higher inside the cell, net diffusion moves it to the outside of the cell. Passive (non-facilitated) diffusion is kinetically slow in the absence of a receptor since membranes present formidable barriers to the passage of polar molecules. - L is a ligand (or substrate S) that binds to a protein enzyme, E. The bound substrate is chemically altered to produce a new product, P, which dissociates from the enzyme. This can be expressed most simply as:
E + S <==> ES <==> E + P .
Consider the mechanism illustrated in Figure \(\PageIndex{7}\).

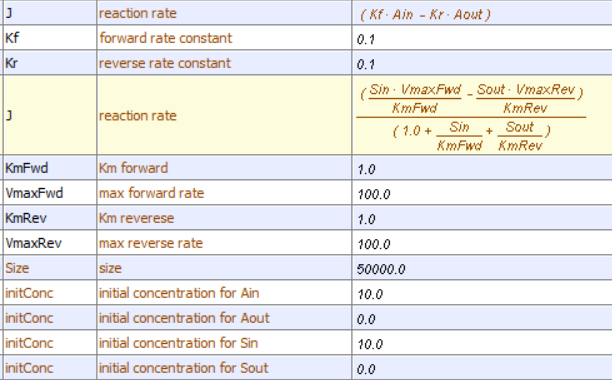
Let's assume that for this system the initial flux will be measured. We would like to derive equations that show J as a function of Aout (assuming that Ain is negligible over the time course of measuring the initial flux. Also, assume that the J facilitated is much greater than J passive. In contrast to passive diffusion, JA is not proportional to Aout but rather to [Abound].
Consider this example to help you understand that proportionality. Pretend that the receptor is a truck that can carry one particle across the membrane at a time (i.e. 1/1 stoichiometry). Also, assume that the particle can't get across without being carried by the truck. If there are no trucks in the membrane, no load can be delivered. If there are trucks in the membrane but no particles in them, no load will be delivered. As the number of particles available to be loaded into the truck increase, the truck will have an increased chance to be loaded (depending of course on the affinity of the particle for the truck). If the number of loaded trucks is doubled, the number of particles dumped to the other side will double. Therefore, by analogy,
JA is proportional to [RA], or
\begin{equation}
J_A=\operatorname{const}[\mathrm{RA}]=\mathrm{k}_3[\mathrm{RA}]
\end{equation}
How can we calculate RA when we know A and R? Let us assume that Atotal (A0) is much greater than R0, as is the likely biological case, and Ain = 0. We can calculate RA using the following equations, and the same procedure we used for the derivation of the binding equation
\begin{equation}
[\mathrm{ML}]=\frac{\left[\mathrm{M}_0\right][\mathrm{L}]}{\mathrm{K}_{\mathrm{D}}+[\mathrm{L}]}
\end{equation}
The equation for the dissociation constant KD
\begin{equation}
\mathrm{K}_{\mathrm{D}}=\frac{[\mathrm{A}]_{\mathrm{eq}}[\mathrm{R}]_{\mathrm{eq}}}{[\mathrm{RA}]_{\mathrm{eq}}}=\frac{(\mathrm{A})(\mathrm{R})}{\mathrm{RA}}
\end{equation}
The equation of mass balance of R
\begin{equation}
\mathrm{R}_0=\mathrm{R}+\mathrm{RA} \text { so } \mathrm{R}=\mathrm{R}_0-\mathrm{RA}
\end{equation}
Since we will assume that A0 is much greater than R0, we will not need the mass balance for A (which is Ao = A + RA).
Substitute x into x and rearrange to get:
\begin{equation}
\begin{gathered}
\mathrm{K}_{\mathrm{D}}(R A)=(A)(\mathrm{R})=(A)\left(\left(\mathrm{R}_0\right)-(A)(R A)\right. \\
\mathrm{K}_{\mathrm{D}}(R A)+(A)(R A)=(A)\left(\mathrm{R}_0\right) \\
\left(\mathrm{K}_{\mathrm{D}}+\mathrm{A}\right)(R A)=(A)\left(\left(\mathrm{R}_0\right)\right. \\
(R A)=\frac{\left(\mathrm{R}_0\right) A}{\mathrm{~K}_{\mathrm{D}}+\mathrm{A}}
\end{gathered}
\end{equation}
Substitute x into z gives the final equation,
\begin{equation}
\mathrm{J}_{\mathrm{A}}=\mathrm{k}_3[\mathrm{RA}]=\frac{\mathrm{k}_3\left(\mathrm{R}_0\right) A}{\mathrm{~K}_{\mathrm{D}}+\mathrm{A}}=\frac{\mathrm{J}_{\max } A}{\mathrm{~K}_{\mathrm{D}}+\mathrm{A}}
\end{equation}
It should be clear to you from this equation that:
- a plot of JA vs A is hyperbolic
- JA = 0 when A = 0.
- JA = Jmax when A is much greater than KD
- A = KD when JA = Jmax/2.
These are the same conditions we detailed for our understanding of the binding equation.
This derivation is based on the assumption that the relative concentrations of A, R, and AR can be determined by the KD for the interactions and the concentrations of each species during the early part of diffusion (i.e. under initial rate conditions). Remember under these conditions, Aout does not change much with time. Is this a valid assumption? Examine the mechanism shown in the above figure. Aout binds to R with a second order rate constant k1. RA has two fates. It can dissociate with a first-order rate constant k2 to Aout + R (to give the original species), or dissociate with a first-order rate constant of k3 to give Ain + R (as A moves across the membrane). If we assume that k2 >> k3 (i.e. that the complex falls apart much more quickly than A is carried in), then the relative ratios of A, R, and RA can be described by KD. Alternatively, you can think about it this way. If A binds to R, most of A will dissociate, and a small amount will be carried across the membrane. If this happened, then R is now free, and will quickly bind Aout and reequilibrate. This occurs since the most likely fate of bound A is to dissociate, not to be carried across the membrane, since k3 << k2.
Note that the JM values for facilitated diffusion are 1000 times the k values for passive diffusion
"Receptors" in Facilitated Diffusion
Two types of proteins are involved in facilitated diffusion, carriers and channels. Carrier proteins (also called permeases or transporters) such as the glucose transporter (GLUT1) move solute molecules across a membrane while channels/pores facilitate the diffusion of ions down a concentration gradient by providing a pore in the membrane. We won't describe in this section the more complicated processes of phagocytosis and endocytosis. These processes are illustrated in Figure \(\PageIndex{8}\).

In the case of permeases and transport proteins, ligands bind and induce a conformational change in the receptor as illustrated in the case of the glucose transport protein shown in Figure \(\PageIndex{9}\).

In channels and pores, a ligand can bind to the receptor (channel protein), which induces a conformational change in the receptor, a "ligand-gated" channel through the membrane. This process would lead to the diffusion of many ions across the membrane (down a concentration gradient) until the channel closes (which can be induced by ligand dissociation or other events).
The mathematics we derived for the carrier proteins does not apply to the channel proteins. In addition, there are other ways to "gate" open a channel protein, which we will discuss later. Also, some transporters can move solute molecules across a membrane against a concentration gradient. These proteins require an external energy source (like ATP or coupling to the favorable collapse of a second transmembrane gradient) to drive this thermodynamically unfavored process. This is called active transport and will be discussed in the next chapter section.
Both links above are from the Theoretical and Computational Biophysics group at the Beckman Institute, University of Illinois at Urbana-Champaign. These molecular dynamic simulations were made with VMD/NAMD/BioCoRE/JMV/other software support developed by the Group with NIH support.
Carrier proteins (permeases or transporters)
Now let's look at some examples of carrier proteins:
Glucose Transport Proteins
Glucose is a key metabolic fuel so its movement into cells is critical and hence highly regulated. There are multiple types of glucose transporters. GLUT 1, a plasma membrane protein, found in most cells, is responsible for constitutive or basal glucose uptake while GLUT 4 is involved in insulin-regulated uptake in skeletal and heart muscles and adipose cells, of glucose after meals. Its official name is solute carrier family 2 or, facilitated glucose transporter member 4. No structure is yet available for GLUT 4 but there is for GLUT1, which is highly expressed in cancer cells that have high energy demands.
Figure \(\PageIndex{10}\) shows an interactive iCn3D model of a glucose transporter, GLUT1 (5eqg), bound to an inhibitor, cytochalasin B (spacefill). The inhibitor binds in the inward-open state where glucose binds.

Mitochondrial ADP-ATP Carrier Protein
We will see in a few chapters that most of the ATP made in cells takes place in the mitochondrial matrix. It won't do cells much good if it stays in there since it is needed in the cytoplasm and elsewhere to drive unfavored processes. Likewise, when ATP is depleted in a cell, ADP is concomitantly high. What is needed is an inner mitochondrial membrane protein that can shuttle ATP out of the mitochondria and ADP in down concentration gradients. It would not make sense to need to power an uphill movement of ATP into the mitochondria from low to high concentration driven by ATP cleavage. Let's look at the structure of the bovine ADP-ATP carrier protein which resides in the inner membrane. Figure \(\PageIndex{11}\) shows an interactive iCn3D model of the bovine mitochondrial ADP-ATP carrier protein (1okc).
.png?revision=1&size=bestfit&width=320)
The transmembrane domain contains six alpha-helices which form a depression leading to the inner leaflet. The cyan spacefill amino acids on the bottom of the depression are RRRMM, which is a motif found in nucleotide carrier protein. A conformational transition must transiently open the depression into a channel. The spacefill molecule in CPK colors represents carboxyatractyloside, a diterpene glycoside that inhibits the carrier protein.
You might guess that free fatty acids, derived for example from lipids after the actions of lipases on triacylglycerol, would not need a carrier protein to move across the cell membrane since they are almost completely nonpolar. Hexanoic acid can indeed pass readily, but for solute diffusion across the membrane, size matters as well. A whole family of proteins, Fatty Acid Transport Proteins (FATPs) have evolved to help long-chain fatty acids across membranes. Human fatty acid transport proteins are transmembrane proteins. Its mechanism of action is unclear. No crystal structures of these are readily available. Many proteins in this class catalyze the formation of fatty acid-CoASH derivatives, which is an endergonic reaction powered by ATP. The mechanism of fatty acid movement across the membrane probably may involve simple diffusion coupled to processes driven by ATP. However, there is still controversy on the role of passive vs facilitated diffusion for fatty acids.
First, let's consider the problems facing a cell in moving fatty acids across two aqueous environments. Figure \(\PageIndex{12}\) shows a mass balance depiction of the reservoirs of fatty acid in the extracellular and intracellular environment.
Free fatty acids are very insoluble in aqueous solution so their concentrations on either side of the membrane are very low, in the low nanomolar range. Hence there is no great thermodynamic drive to move free fatty acids across the membrane. If you assume that fatty acids can reasonably transverse the membrane without a carrier protein, there would be no huge kinetic barriers to movement except their low concentrations.
On each side of the membrane, the free fatty acids are in an "equilibrium" with protein-bound amino acids. In the blood and interstitial fluids, albumin, which can bind multiple fatty acids, is in high concentration, so it can act as a buffer to keep free fatty acids in a useful concentration range. Likewise, in the cytoplasm, fatty acid binding proteins (FABPs), which typically bind just one fatty acid, are also relatively high in concentration and buffer the free fatty acids in the cytoplasm. One other note. Free fatty acids are single-chain amphiphiles which makes them detergents, which could easily lyse cell membranes, so their free concentrations must be kept very low compared to the critical micelle concentration.
Figure \(\PageIndex{13}\) shows an interactive iCn3D model of the human brain fatty acid-binding protein bound to docosahexaenoic acid (1fdq).
.png?revision=1&size=bestfit&width=180)
How do long-chain fatty acids cross the membrane? We will first examine the role of proteins. Let's look at a couple of players.
Fatty acid transport proteins (FATPs): There are six members of the human FATP family, which is also known as the Solute carrier family 27. FATP 1 (SLC27A-1) is found in plasma and endoplasmic reticulum membranes and based on sequence analysis it is a single-pass membrane protein. Its highest expression is in muscle and adipose cells. It possesses a C-terminal AMP binding domain and acyl-CoA synthase activity. The mouse protein has an N terminal transmembrane domain and predictions from the human sequence show there is likely just one transmembrane helix at the N terminus (amino acid 13-35). Given that, and the absence of a 3D structure, it would appear that this protein would not bind and transfer the bound lipid across the membrane through a conformational change in the transmembrane domain. FATP 4, located in the ER membrane, is predicted to have 2 transmembrane helices, which still would probably be inadequate to serve as a class translocase. It is expressed in the endoplasmic reticulum cell membrane.
Platelet Glycoprotein 4 (CD36): Another candidate is platelet glycoprotein 4, which is also called CD36, Glycoprotein IIIb, fatty acid translocase, or the thrombospondin receptor. The protein has many functions and binds many types of proteins (thrombospondin, fibronectin, collagen or amyloid-beta) and lipids (oxidized low-density lipoprotein (ox-LDL), anionic phospholipids, long-chain fatty acids, and bacterial diacylated lipopeptides). It is present in plasma and Golgi membranes. Sequence analysis shows that it passes through the membrane twice (amino acids 7-29 and 441-463) and it also is palmitoylated at both N- and C-terminal ends. A PDB structure (5LGD) for most of the protein except the putative N- and C-terminal helices are known. In the structure, it is bound to a malarial protein (shown in grey) and two palmitic acids (spacefill) bound in the nonmembrane domains. Again, from this description, it doesn't appear that the bound fatty acids are translocated via a conformational change in the receptor as described above for glucose and ADP/ATP.
Fatty Acid Binding Proteins (FABPs): These proteins might also take part in the process. In addition to the cytoplasmic form, there is also a plasma membrane-associated fatty acid-binding protein (FABPpm), also known as FABP-1. It's the same protein as mitochondrial aspartate aminotransferase (UniProtKB - P00505 (AATM_HUMAN). It has many possible functions.
Figure \(\PageIndex{14}\) shows a possible model for how fatty acids may transfer or be handed off from albumin to membrane-bound GP36 or FATP-1, possibly through an intermediary protein like FABPpm (for GP36).
Some proteins (albumin, FABP) deliver fatty acids to the membrane proteins (CD36, FATP-1), which deliver free fatty acids into the outer leaflet, where they flip to the inner leaflet, where they are picked up by membrane-associated cytoplasmic fatty acid binding proteins (FABP). Until structures are known for the transmembrane-bound proteins GP36 and FATP-1, whose full amino acid sequences don't suggest a classic carrier protein, this mechanism is a reasonable one. FATP-1 has acyl-CoA synthase activity so it is likely that the transferred fatty acid is converted to the acyl-CoASH before movement to the cytoplasm. Fatty acid transporters are also implicated in insulin resistance and type 2 diabetes.
The alternative model proposes that long-chain fatty acids, the preferential energy source for cardiac muscle, can cross the membrane by passive diffusion (red boxed area above) even if the activity of CD36 is inhibited. Diffusion depends on an alteration of the pKa of outer membrane adsorbed free fatty acids (around 7.5) compared to free fatty acids in solution (around 4.5). The protonated fatty acid adsorbed to the membrane would move into the outer leaflet where it would flip to the inner leaflet and be picked up by cytoplasmic and/or peripheral membrane proteins. This process would be associated with movement of H+ across the leaflet as well. This type of diffusion has been observed in protein-free lipid vesicles and cells. Likewise, long chain fatty amines (instead of carboxylic acids) can diffuse into vesicles and cells which would support this passive diffusion if fatty acid-binding proteins don't bind the amine forms.