11.3: Diffusion Across a Membrane - Channels
- Page ID
- 59156
Introduction
If you punched a hole or pore in the membrane, depending on its size, multiple types of chemical species could flow through it simultaneously. We'll talk about pores in the next section. Let's focus on channels, which have much smaller openings, which are gated open to allow ion flow through them. They are often called ionotropic receptors. Channels can be "gated" open by many mechanisms including ligand binding, change in membrane potential, lipid interactions, and mechanical stress. Opening a channel to ion flow allows quick passage of information (in this case an electrical signal) into the cell, leading to quick cellular responses. This is an ideal signaling mechanism for neural cells which demand quick responses.
We'll show examples of each type of gating mechanism. Before we do, it is helpful to know typical extracellular and intracellular ion concentrations in a mammalian neuron, for example (Table \(\PageIndex{1}\)).
| ion | extracellular = [ion]out (mM) | intracellular = [ion]in (mM) |
|---|---|---|
| Na+ | 145 mM | 5-10 mM |
| K+ | 5 mM | 140 mM |
| Cl- | 110 mM | 10 mM |
| Ca2+ (free) | 1.2 mM | 100 nM |
When ion channels are opened in neural cell membranes, the direction of favorable thermodynamic flow is down a concentration (chemical potential) gradient but the direction is also affected by the transmembrane potential. Typical resting potentials of neural cells are about -60 to -70 mV (negative inside). If a nonspecific cation channel is gated open, the kinetic barriers to diffusion are relieved and at that moment Na+ ions would flow in due to both the chemical and electrical potential, while K+ ions would flow out but with less driving forces since its efflux is hindered by the negative transmembrane potential. How are such large gradients of these ions formed? We'll answer that in the next section on active transport.
Pentameric ligand-gated ion channels (pLGICs)
These channels play a key role in neuronal signaling. They are ligand-gated channels. In neural systems, the ligands are neurotransmitters. All are comprised of five monomers, which together form the functional channel with the pore formed in the center of the pentameric structure. The subunits can be identical (homopentamer) or different (heteropentamer). All have "Cys-loop" motifs so they have been called Cys-loop receptors as well. Examples include the mammalian nicotinic acetylcholine, serotonin (5-HT), γ-aminobutyric (GABA), glycine, and glutamate receptors.
Figure \(\PageIndex{1}\) shows the generic structure of the pLGICs
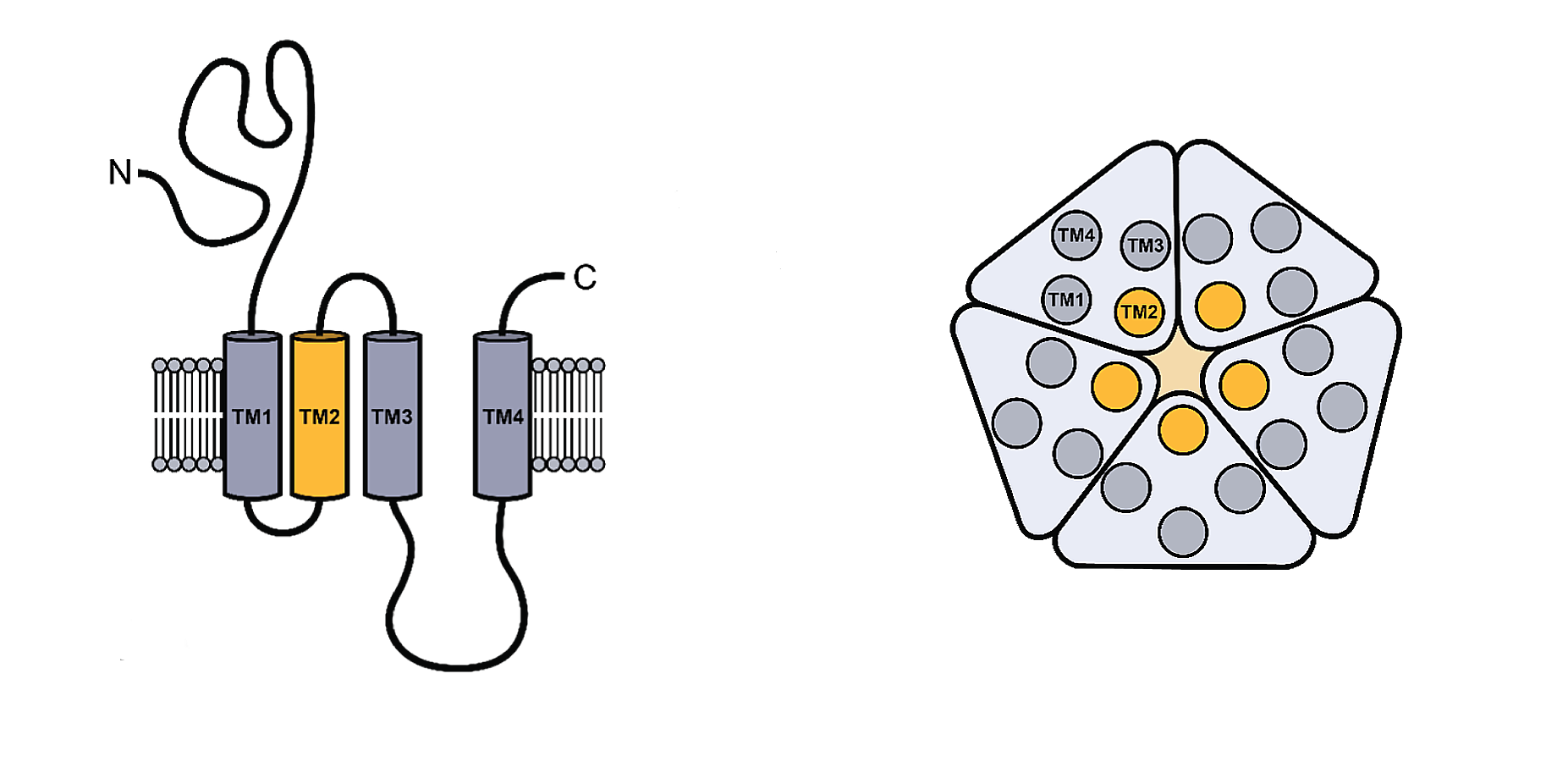
The monomeric structure is shown on the left. Each contains four transmembrane helices (TM1-4). A top-down view of the pentameric structure is shown to the right. The pore surface forms at the interface of the central TM2 helices. The ligand (neurotransmitter) binds to the extracellular domain with contributions from all the subunits. On ligand binding, TM2 and TM3 rearrange to allow the formation of a transient pore and passive diffusion of specific ions.
pLGICs are incredibly interesting and pharmacologically relevant. In general, they have two different types of binding sites.
Orthosteric sites bind ligands in the extracellular domains. When bound, a conformational change leads to the rearrangement of helices opening the pore. The natural ligand is also called the agonist as it promotes the function (either neuron excitation or inhibition) of the ion channel. The binding of the natural ligand/agonist opens up the channel to ion flow. This can lead to activation or excitation of the neural cell if positive cations flow into the cell, which depolarizes the cell as the transmembrane potential becomes more positive. Neurotransmitters that lead to this response are excitatory. Alternatively, the binding of inhibitor neurotransmitters in the orthosteric site can lead to inhibition of the neural cell activation if the channel is a ligand-gated anion channel. This hyperpolarizes (makes the transmembrane potential more negative), leading to inhibition of neural cell activation. Inhibitors or antagonists of channel function, whose structure typically resembles at least somewhat the structure of the endogenous ligand or agonist, also bind to the orthosteric site.
Allosteric sites are distal to the orthosteric site. Ligands that bind to allosteric sites also lead to conformational changes that either augment or diminish the effect of normal ligand/agonist binding by modulating ion flow through the pore.
pLGICs interact with analgesics and anesthetics which makes them even more interesting.
Figure \(\PageIndex{2}\) shows two excitatory pLGICs, the 5-hydroxytryptamine (5HT) (left) and nicotinic acetylcholine (right) receptors. The ligand binds in an orthosteric site in the extracellular domain (ECD), which is composed mostly of beta secondary structure. Allosteric sites are often found in the transmembrane domain.
Likewise, Figure \(\PageIndex{3}\) shows orthosteric binding sites for GABA and glycine, as well as the binding of modulators that can bind in the TMD or, in the case of benzodiazepines in the ECD as well.
The actual mechanisms of how anesthetics work are still unclear. These fascinating molecules can alter function in a variety of organisms including bacteria, yeast, worms, flies, and plants, as well as animals. Of course, their effect on consciousness appears to be found only in animals. Their selective "turning off" of a function (consciousness) of an entire organ (the brain) is stunning! One theory suggests that they exert their effects through bulk changes in the lipid bilayer, as the potency of anesthetics is generally related to their hydrophobicity. Most are nonpolar and have long been known to work on membranes, presumably altering ion flow through neural membrane ion channels. Typical inhalational and intravenous anesthetics are shown in Figure \(\PageIndex{3}\), along with their date of first use.
Figure \(\PageIndex{3}\): Structure of common inhalational and intravenous anesthetics. Adapted from Eur J Anaesthesiol. 2009 Oct; 26(10): 807–820. doi: 10.1097/EJA.0b013e32832d6b0f
A very robust correlation is found between the minimum alveolar concentration (MAC, in atmospheres) of inhalational anesthetics and their partition coefficient into olive oil (a measure of their hydrophobicity). This is illustrated in the Meyer-Overton plot shown in Figure \(\PageIndex{3}\).
Figure \(\PageIndex{3}\): The Meyer-Overton plot of minimum alveolar concentrations (in atmospheres) vs partition coefficient into olive oil for inhalation anesthetics. https://commons.wikimedia.org/wiki/F...orrelation.png
The MAC is the concentration of inhaled anesthetic within the alveoli at which 50% of people do not move in response to a surgical stimulus (i.e. it is much like an IC50 for receptor inhibition). What's so fascinating is the range of molecular species, including N2 and most Noble gases, that can act as anesthetics. Consider N2, a nonpolar and nonreactive molecule, which comprises 80% of the atmosphere. From the graph, it is evident that it takes high pressure for it to exert its anesthetic properties. That can occur when scuba diving using regular air in tanks. Divers can experience nitrogen narcosis (also called depth intoxication or rapture of the deep) when using just compressed air. Hence a mixture of 21% oxygen, 35% helium, and 44% nitrogen is often used. Nitric oxide is used by dentists to alter consciousness and pain perception but does not cause general anesthesia except in some who can be hypersensitive to its use.
Additional studies suggest protein:anesthetic interactions are important. For example, the activity of the water-soluble protein luciferase is affected by them. Some molecules (like dichlorohexafluorocyclobutane), expected to have anesthetic properties based on their hydrophobicity, don't. The (S) enantiomer of isoflurane is 50% more potent than the (R) enantiomer in rats, which is hard to explain based on nonspecific partitioning into a bilayer.
Most modern theories suggest that they more directly affect specific target proteins and their proximal interacting lipids in neuromembrane bilayers. The main targets of anesthetics appear to be pLGICs. Anesthetics reduce neuron excitability and firing. Hence you could hypothesize that they inhibit excitatory pLGICs (such as the 5HT and acetylcholine receptors) and/or activate inhibitory ones such as the GABA and glycine receptors. pLGICs are pharmacological targets of many general anesthetics. However, anesthetic inhibition of certain GABA channels and potentiation of nicotinic acetylcholine channels have also been observed.
Recent elegant studies have shown that the inhaled anesthetic chloroform and isoflurane affect K+ ion flow through the potassium channel subfamily K member 2, known also as the outward rectifying potassium channel protein TREK-1. The channel converts between a voltage-insensitive potassium leak channel and a phosphorylated voltage-dependent outward rectifying potassium channel. It doesn't affect the channel protein directly but indirectly through alteration in the local membrane which affects the location of phospholipase D2 (PLD2), a protein anchored to the membrane by covalent attachment of palmitic acid. PLD2 hydrolyzes phosphatidylcholine, with a positively charged choline head group, to choline and phosphatidic acid, with a negatively charged phosphate head group
The effect of these general anesthetics appears to be on lipid rafts in neural membranes. Lipid rafts are enriched in cholesterol and saturated lipids, especially sphingomyelins such as monosialotetrahexosylganglioside1 [GM1]. Rafts are especially important in the brain where cholesterol can reach up to 45% of plasma membrane lipids. Typical rafts are about 100 nm in diameter. In the presence of hydrophobic anesthetics, the rafts become larger and more dispersed, as the anesthetic partitions into them.
Membrane proteins also partition into rafts. One such protein is phospholipase D2 (PLD2), which is targeted to the inner leaflet rafts by post-translation palmitoylation. In the presence of general anesthetics, the PLD1 laterally translates away from the disrupted and enlarged lipid raft and binds to a disordered C-terminal region of the TREK-1 protein. This localizes the PLD2 and helps activate it to produce high local concentrations of phosphatidic acid with its negatively charged head group. That group interacts with a positive region of the TREK-1 protein, inducing a conformational change in the channel which opens it to K+ efflux. In effect, PLD2 activates TREK-1 through the local formation of phosphatidic acids.
The opening of the channel hyperpolarizes the cell membrane (making the inside more negative, and inhibiting neural activity (a hallmark of anesthesia). These concerted actions are shown in Figure \(\PageIndex{a}\) below.
Deletion of the TREK-1 gene decreases the effect of the anesthetics. If a catalytically inactive mutant of PLD2 (K758R) is overexpressed, all effects of chloroform were eliminated.
We will now explore two pLGIC, the eukaryotic nicotinic acetylcholine channel, and a prokaryotic analog, GLIC.
Nicotinic acetylcholine channel (6cnj)
One very interesting channel is the one involved in nicotine addiction. It binds nicotine (an exogenous alkaloid) and the normal endogenous neurotransmitter, acetylcholine. Both compete for the same orthosteric binding site. Since the binding of nicotine gates open the channel, nicotine acts as an agonist. The similarities in their structures are illustrated in Figure \(\PageIndex{4}\).
The membrane protein is a ligand (acetylcholine)-gated (open-close) positive ion (Na+ or K+) channel, involved in fast neural communication (such as at the neuromuscular junction). The quaternary structure of the pentameric receptor consists of two α4 and three β2 subunits - (α4)2(β2)3. This isoform is the most abundant in the human brain and the one involved in nicotine addiction.
The iCn3D model (6CNJ) below has two bound nicotines (spacefill) in the extracellular domain and one Na+ ion (spacefill) in the transmembrane domain containing the pore. The Na+ or K+ ions flow across the membrane down a concentration gradient in a thermodynamically favored process.
Figure \(\PageIndex{5}\) shows an interactive iCn3D model of the nicotinic acetylcholine channel with two bound nicotines (spacefill) in the extracellular domain and one Na+ ion (spacefill) in the transmembrane domain containing the pore (6CNJ). (long load time)
.png?revision=1&size=bestfit&width=260)
The Na+ or K+ ions flow across the membrane down a concentration gradient in a thermodynamically favored process.
The gold, blue, and brown β2 subunits are glycosylated on Asn 143 and are shown with a Man (β4) GlcNAc (β4) GlcNAc N-linked oligosaccharide. Nicotine is bound between two alpha-beta interfaces. One is shown between the green (alpha) and gold (beta) subunits and the other is between the magenta (alpha) and blue (beta) subunits.
GLIC: A prokaryotic pLGIC
This protein is a proton-gated cation channel with specificity for both Na+ and K+, which diffuse down their electrochemical gradients. In a sense, H+s in the extracellular side act as "ligands" as the channel is opened with increasing H+ concentration (decreasing pH) on the outside of prokaryotic cells. The protein is homologous to eukaryotic pLGICs. Structures of the protein from Gloeobacter violaceus bound to propofol, an anesthetic, are known. GLICs also interact with ethanol and barbiturates as well. Hence they serve as models to elucidate the binding and effects of anesthetics.
In contrast to eukaryotic pLGICs, the "ligand - H+" does not bind in the orthosteric site in the extracellular domain occupied by traditional ligands. Rather changes in protonation states of key proton acceptors and donors in the protein lead to conformational changes analogous to those found on binding ligands to orthosteric sites on classical pLGICs. The external pH associated with half-maximal inward current, pH50 is approximately 5.1 ± 0.2.
Evidence suggests that when pH is lowered from 7 to 4, Glu 35 (distant from the orthosteric site), with a pKa - 5.8, becomes protonated. It connects through other H+ acceptors and donors in the open form through a hydrogen bond network. These include two triads of amino acids found at the interface between the extracellular (ECD) and transmembrane (TMD) domains. R192-D122-D32 comprise a conserved "electrostatic triad". The second is Y197-Y119-K248. The network allows bridging of the effects starting with Glu 35 in the ECD into the transmembrane region where allosteric effectors usually interact with the protein.
Figure \(\PageIndex{6}\) shows an interactive iCn3D model of the open form of GLIC (3P50) with bound propofol (long load time)
.png?revision=1)
Orient the iCn3D model below with the extracellular domain (mostly beta structure) at the top and the transmembrane domain (alpha-helical) at the bottom. Key molecular players involved in the interactions described above, from the top down:
- Glu 35 (stick, color CPK)
- R192-D122-D32 electrostatic triad (sphere, CPK color)
- Y197-Y119-K248 triad (stick, color magenta)
- propofol (sphere, color CPK)
Propofol and another anesthetic, desflurane, bind at the same site localized in the upper part of the transmembrane domain of each of the five subunits.
The model below shows the mostly nonpolar (induced dipole-induced dipole) interactions between one bound propofol and side chains in the TMD. Also shown is an interaction between phosphatidylcholine and propofol.
Figure \(\PageIndex{7}\) shows an interactive iCn3D model showing the mostly nonpolar (induced dipole-induced dipole) interactions between one bound propofol and side chains in the TMD. Also shown is an interaction between phosphatidylcholine and propofol. (long load time)
.png?revision=1)
Voltage-Gated Ion Channels
In contrast to pentameric ligand-gated ion channels, which require 5 monomeric subunits to aggregate into a quaternary structure to form a pentameric pore, voltage-gated ion channels can form a channel from an aggregate of monomeric proteins, each containing a single 6 transmembrane helical unit, or from a longer polypeptide containing multiple repeating 6 transmembrane helical units.
Figure \(\PageIndex{8}\) shows a cartoon of a common voltage-gated K+ channel. The monomer (top), denoted as the α subunit, contains a transmembrane domain containing 6 helix segments. Four of these monomers aggregate to form the actual homo- or heterotetrameric channel (bottom).
The genes for the Kv channel family, which facilitate K+ diffusion across the membrane, encode α subunits of approximately 500 amino acids and a molecular weight of about 57,000. Four of these α subunits come together in the membrane to form the functional channel, a tetramer of α subunits, which together make one central pore. The α subunit can form homo- or heterotetramers since there are different α subunit encoding genes. In addition, the functional channel has smaller, regulatory β subunits as well.
A cartoon structure of a typical voltage-gated Na+ channel is shown in Figure \(\PageIndex{9}\). It is a single polypeptide (α) chain that contains 4 sequential repeats of the 6 transmembrane helical segments (I-IV). The functional channel (bottom) has just one polypeptide chain.
The Na+ channel has a molecular weight of around 229K and about 2000 amino acids (each 4x that of the K+ channel α subunit). It is glycosylated and subjected to multiple post-translational modifications. Usually, the protein in the central nervous system is a complex of the α subunit, and small additional regulatory β subunits, which modify the kinetics and voltage-dependency of the α subunit channel.
Segment (helix) 4 of each of the four repeat units illustrated above is the conserved "voltage" sensor. It contains multiple, charged amino acids whose disposition changes with changes in the transmembrane potential, allowing conformational changes in the protein and gating of ion flow. Each of the 4 repeating units above also contains an extracellular P-loop (colored purple in segment I in purple) connecting helix 5 and helix 6.
We will focus on K+ channels with some additional information on the Na+ channel below.
K+ Permeation through Kv1.2 Channel
Voltage-dependent potassium channels (Kv) have 4 subunits and can be homo- or heterotetramers. They allow the voltage-gated flow of potassium ions through the membrane. Several obvious questions should arise. How can they be selective for K+ ions? That is, how can they allow the larger K+ ion to passively flow through and not the smaller Na+ ions? Secondly, how can a change in the transmembrane potential cause the channel to open or close? That question boils down to how a change in transmembrane potential can change the conformation of proteins. We'll show several iCn3D models of this protein.
Figure \(\PageIndex{10}\) shows a simplified view of the rat Kv1.2 channel (3lut) from top and side views (without parts of the cytoplasmic domain), showing each of the 4 identical monomeric subunits in a different color. Each monomer has S1-S6 transmembrane segments.
The protein is found in the brain and central neuron plasma membranes and also in the cardiovascular system. K+ ions diffuse through the center from the extracellular to intracellular side down a concentration gradient but potentially against the transmembrane potential. The four monomers in the homotetramer form one central pore.
Figure \(\PageIndex{11}\) shows an interactive iCn3D model showing the rat Kv1.2 channel (3lut) described in Figure \(\PageIndex{10}\).
.png?revision=1&size=bestfit&height=135)
Figure \(\PageIndex{12}\) shows an interactive iCn3D model showing the S4 voltage sensor helix in each monomer of the Kv1.2 potassium channel (3lut) .
%25C2%25A0.png?revision=1)
Figure \(\PageIndex{13}\) shows a more detailed structure of the Kv1.2 potassium channel (3lut). The four monomers, which pack together to form the tetramer, are shown in light and dark grey to allow key residues highlighted in color to stand out. The details are explained below.
The left images show the channel from the side (top left view) and top (bottom left view). The right images show just one of the monomers with different side chains highlighted.
Figure \(\PageIndex{14}\) shows an interactive iCn3D model detailing key residues in the workings of the Kv1.2 potassium channel (3lut)
.png?revision=1)
K+ selectivity - All potassium ion channels, even if not voltage-gated, solve the selectivity dilemma in a similar way. All have in the narrowest part of the pore in the center of the channel this consensus sequence - Thr-Thr-Val-Gly-Try-Gly (TTVGYG) - which is found in the P-loop. These are shown in gold and brown colors in the figure above. The -OHs in the selectivity filter can interact with a dehydrated K ion but not with a dehydrated Na ion, which can not approach close enough to form significant interactions. Surrounding the filter are twelve aromatic amino acids which constrain the size of the pore opening. The interactions of the filter O's with the K ion make up for the energetically disfavored dehydration of the ion. The filter contains K+ ions which repel each other, assisting in the vectorial discharge of the ions through the membrane. These ions must form weak interactions with the selectivity filter. The actual pore is mostly hydrophobic, which facilitates ion flow through the membrane.
Figure \(\PageIndex{15}\): below shows a closeup of the selectivity filter. Four Thr 374s (second Thr in the selectivity filter sequence of TTVGYG) from the four different monomers in the channel are clearly shown interacting with the top K+ ion (gray sphere).
Figure \(\PageIndex{16}\) shows an interactive iCn3D model detailing key residues in the K+ selectivity filter of the Kv1.2 potassium channel (3lut). Hover over the residues to identify them.
%25C2%25A0.png?revision=1)
Different voltage-gated ion channels alter ion selectivity through changes in these amino acids in the P-loop, as illustrated in Table \(\PageIndex{2}\) below. As channels lose specificity of K+, they gain specificity for Na+ and Ca2+. Red highlights denote conserved residues and yellow residues that are chemically similar.
| sequence | specificity |
| TVGYG | strong K+ channels |
| CIGYG | weak K+, HCN channels |
| TVGDG | TRP channels |
| STFEG | ionotropic glutamate receptors |
| LCGEW | strong Ca2+ voltage-gated channels |
Table \(\PageIndex{2}\): P-loop specificity side chains in voltage-gated ion channels
Voltage gating -
Helix S4 in each monomer in the transmembrane domain of the complex is the voltage sensor. The sequence of this helix is LAILRVIRLVRVFRIFKLSRH. Note the arginines and lysine highlighted in blue. They repeat every 3 amino acids. The voltage-sensor domain must be shielded from the nonpolar acyl of the bilayer. Four conserved Arg residues on S4, part of the voltage-sensor domains, are shielded from the lipids and coupled to an amphiphilic helix running parallel to the plane of the membrane. The arginines move under the influences of forces arising from changes in the membrane's electric field initiated by ion movement through other ion channels in the membrane. Mechanical work is done by the electric field on the voltage sensor as the charged Arg residues are moved through the electric field. The movement is coupled through the amphiphilic helix to the pore which changes conformation. In turn, the S4 and coupled S5 helices of the voltage sensor do mechanical work on the pore by altering its conformation to open/close the pore, specifically at the activation gate of the pore. This seems quite similar to how iron movement into the heme plane in hemoglobin on oxygenation pulls the proximal His on the F8 helix which then transmits a conformation change to other helices in the subunit, leading to cooperative conformational changes in the tightly packed protein. About 12 charges move across the transmembrane potential field.
Channels, once open, must be inactivated. In the case of the voltage-gated potassium channel, inactivation occurs when the amino-terminal cytoplasmic domain binds to the potassium pore on the cytoplasmic side, in interaction likened to the binding of a "ball on a chain" (the cytoplasmic domain) to the pore opening. The chain acts to tether the ball domain so it may swing to bind to the pore opening. The ball domain contains both positively charged and hydrophobic regions. Where is the ball domain in the absence of inhibition? Recent studies (Oliver et al.) have shown that a positive domain can bind to proximal phosphatidyinositol 4,5-bisphosphate (PIP2) lipids on the inner leaflet of the membrane bilayer. When so bound, inactivation of the channel is prevented. As you will see in the next section, PIP2 can also be cleaved to form diacylglycerol and inositol 1,4,5-trisphosphate when cells are activated by external factors (hormones, growth factors, etc) in the process of signal transduction.
Figure \(\PageIndex{17}\) shows a molecular dynamics simulation showing K+ interaction with the channel lining and the "knock-on" mechanism showing how an incoming K+ ion can repel a K+ ion in the pore through the channel.
Figure \(\PageIndex{17}\): Molecular dynamics simulation of K+ movement through a channel
Recent Updates: June 2023 - Sodium Channels
Voltage-gated sodium channels (NaV)
The eukaryotic voltage-gated sodium channels (NaV) allow inward movement of Na+ ions which depolarizes a neuron and sets off an action potential in nerve and muscle cells. (For more information on neuron signaling, see Chapter 28.9). The NaV has an alpha subunit that forms the pore plus beta subunits that associate with it and modulate its activity. Nine eukaryotic isoforms exist. NaV has 4 domains, I-IV, each containing segments 1-6. Each of the S1-S4 segments forms a voltage-sensitive domain and each of the S5 and S6s form the pore. In contrast to eukaryotic NaVs which have a single chain, bacterial NaVs contain 4 identical subunits. Post-translation modification of the alpha subunit can regulate its activity.
As important as it is to initiate Na+ influx to trigger neuron firing, it is equally important to turn it off to control neural signaling. The inward Na+ current is stopped by a fast inactivation that occurs within a few milliseconds.
Many neurotoxins bind to the NaV and regulate its activity. Key examples are the α-scorpion and sea anemone toxins which both inhibit the fast inactivation of the NaV leading to prolonged or sequential action potentials. These toxins binds to the voltage sensor in domain IV which is key for the fast inactivation in the absence of the toxin.
The S4 helical segments in each domain are the key voltage sensors. Each of the S4 segments has 4-6 positively charged Arg and Lys side chains. On depolarization of the cell (when the inside becomes less negative and more positive), this helix move "up" from the cytoplasmic side (which is increasingly more positive) which opens voltage-gated channel. Specificity for the small Na+ ion (over the K+ and Ca2+ ions) is determined mainly by 4 amino acids, DEKA (Asp-400, Glu-755, Lys-1237, and Ala-1529) found in P loops of domain I-IV, respectively. This selectivity filter is conserved.
Figure \(\PageIndex{18}\) below shows a cartoon of the NaV with two associated, regulatory beta chains.
Figure \(\PageIndex{18}\): Cartoon of eukaryotic voltage-gated sodium channel (Nav) with two associated, regulatory beta chains. https://www.guidetopharmacology.org/...rd?familyId=82. CC BY-SA 4.0
Note the sites for posttranslational modification by phosphorylation and drug interactions. Cylinders represent probable α-helical segments S1-S6. Bold lines represent the polypeptide chains of the selectivity filter and tetrodotoxin binding site; The yellow S4 segments are the voltage sensors. The "h" in the blue circle is in the inactivation gate loop. Blue circles are sites implicated in forming the inactivation gate receptor. Sites of binding of α- and β-scorpion toxins (ScTX) and a site of interaction between α and β1 subunits are also shown. Tetrodotoxin is a specific blocker of the pore of sodium channels, whereas the α- and β-scorpion toxins block fast inactivation and enhance activation, respectively, and thereby generate persistent sodium current that causes depolarization block of nerve conduction.
Table \(\PageIndex{3}\) shows the different types of neurotoxin receptors sites found in NaVs
| Neurotoxin Receptor Site # | Toxin or Drug | Domains |
| 1 | Tetrodotoxin | IS2–S6, IIS2–S6 |
| Saxitoxin | IIIS2–S6, IVS2–S6 | |
| µ-Conotoxin | ||
| 2 | Veratridine | IS6, IVS6 |
| Batrachotoxin | ||
| Grayanotoxin | ||
| 3 | α-Scorpion toxins | IS5–IS6, IVS3–S4 |
| Sea anemone toxins | IVS5–S6 | |
| 4 | β-Scorpion toxins | IIS1–S2, IIS3–S4 |
| 5 | Brevetoxins | IS6, IVS5 |
| Ciguatoxins | ||
| 6 | δ-Conotoxins | IVS3–S4 |
| local anesthetic drug sites | Local anesthetic drugs | IS6, IIIS6, IVS6 |
| Antiarrhythmic drugs | ||
| Antiepileptic drugs |
Table \(\PageIndex{3}\): Neurotoxin receptor sites in NaVs. https://www.guidetopharmacology.org/...rd?familyId=82. CC BY-SA 4.0
A view of the effective pore in the bacterial Nav is shown below in Figure \(\PageIndex{19}\).
Figure \(\PageIndex{19}\): Structure of the bacterial sodium channel NavAb pore B. Architecture of the NavAb pore. Glu177 side-chains in the P loop are shown in purple. The pore volume is shown in grey. The P and P2 alpha helices that form the scaffold for the selectivity filter and outer vestibule are shown in green and red, respectively. https://www.guidetopharmacology.org/...rd?familyId=82. CC BY-SA 4.0
As mentioned above, the bacteria NaVs have 4 monomeric subunits. In contrast to the K+ channel, which requires the K+ ions to be dehydrated to make sufficient interactions with the pore and to pass through, the Na+ ions need to be hydrated. Figure \(\PageIndex{20}\) shows an interactive iCn3D model of the A and B chains of the bacterial NaV voltage-gated sodium channel pore and C-terminal domain (5BZB)
Figure \(\PageIndex{20}\): A and B chains of bacterial NavMs voltage-gated sodium channel pore and C-terminal domain (5BZB)
(Copyright; author via source). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...vRmDqmDHGsYLh8
One subunit is shown in a transparent cyan surface and the second one is shown in magenta. Three Na+ ions are shown (gray spheres). Eight water molecules are shown interacting with them in the pore. The other two subunits are not shown for clarity.
The voltage-gated sodium channel has three major conformational states:
- a basal closed state found at resting cell potentials in which the pore of Na+ is occluded by an activation gate
- an open state found when a depolarizing potential is reached in the cell
- an inactivated state formed within 10 ms of opening of the channel when the inactivation gate with a a Ile-Phe-Met (IFM) sequence motif, found in the intracellular linker between domain III and IV (near the cytoplasmic face of the receptor) closes off the pore to further Na+ entry.
The protein converts back to the closed state when the transmembrane potential is restored to its initial value (around -70 mV) and the positively charged S4 segments move back towards the cytoplasmic face.
A cartoon of the three-state model for the Na+ channels (as other voltgage-gates ion channels in general) is shown in Figure \(\PageIndex{21}\) below.
Figure \(\PageIndex{21}\): Three-state model for the voltage-gated ion channels. Hinard, Valerie & Britan, A & Rougier, Jean-Sébastien & Bairoch, Amos & Abriel, Hugues & Gaudet, Pascale. (2016). ICEPO: The ion channel electrophysiology ontology. Database : the journal of biological databases and curation. 2016. 10.1093/database/baw017. Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0/)
The YouTube video by Pete Meighan below shows an incredibly clear description of the three conformational states of the channel and the conversion from closed to open to inactivated states.
To understand these conformations states, we need to look a the structure of the protein in greater detail. Figure \(\PageIndex{22}\) below shows multiple representations of the voltage-gated sodium channel. The pore domain PD is formed from helix segments 4 and 5 on each of the IV domains of the protein. The voltage sensor domain is formed from the S1-S4 segments, of which segment S4, containing multiple positively-charged Arg and Lys, is key.
Figure \(\PageIndex{22}\): Structure features of the voltage-gated sodium channel. Dongol, Y.; C. Cardoso, F.; Lewis, R.J. Spider Knottin Pharmacology at Voltage-Gated Sodium Channels and Their Potential to Modulate Pain Pathways. Toxins 2019, 11, 626. https://doi.org/10.3390/toxins11110626. Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
Panel (A) shows a schematic representation of the α-subunit of voltage-gated sodium (NaV) channel. Four non-identical domains (DI–DIV) feature six neurotoxin receptor sites (Sites 1–6) and key residues contributing to the outer Na+ ion selectivity filter (EEDD) and inner selectivity filter (DEKA). The connecting S5–S6 linker is called P-loop (P) which together with S5 and S6 segments from each domain contributes to the formation of the Na+ ion selective channel pore. Sites 1-6 (colored purple, green, cyan, magenta, etc) are sites where inhibitors such as toxins bind.
Panel (B) shows the structure of the NaV1.7 channel (PDB 6J8G). Four voltage sensing domains (VSDs), DI (yellow), DII (blue), DIII (green), and DIV (orange), are shown with their corresponding pore-forming segments (S5 and S6) arranged to form the pore domain (PD) selective to Na+ ions. The P-loop that contributes to forming the inner selectivity filter is colored in red spheres (DEKA) and outer selectivity filter (EEDD) is colored in purple. The S6 segments of all the four domains contribute to form the intracellular region of the pore. Site 3 (cyan) and Site 4 (pink) are the major binding sites for spider knottins (neurotoxins). The β1 and β2 subunits which interact with DIII and DI, respectively, are highlighted in beige color.
Panel (C) shows a schematic of the three main conformational states of the protein which control gating of NaV channels. At polarized potentials, the DI–DIV S4 segments are drawn towards the intracellular side due to the positive gating charges to render the closed conformation (down state). Upon depolarization, the forces holding the down state are relieved and DI–DIII S4 segments are rapidly released extracellularly to open the S6 channel gate in the open conformation (up state). Note the movement of the S4 helix with its positive charged toward the extracellular side of the membrane. The DIV S4 moves up slowly compared to DI–DIII S4 and drives the fast inactivation, where the channel is occluded intracellularly by the Ile, Phe, and Met (IFM) motif. After cell repolarization, the channel returns to a closed (resting) state.
Figure \(\PageIndex{23}\) shows an interactive iCn3D model of a ternary complex of human Nav1.2 with the beta2 regulatory subunit and conotoxin IIIA (6J8E)
Figure \(\PageIndex{23}\): Human sodium channel Nav1.2-beta2-KIIIA ternary complex (6J8E)
(Copyright; author via source). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/icn3d/share.html?aYxomdUqZHqbMmE5A
Domains I-IV are shown in gray, yellow, green and cyan, respectively. The separate beta-2 regulatory subunit is shown in magenta. The positive side chains in each of the S4 segments of the four domains are shown as red sticks. The side chains of the inner 4 amino acids (DEKA) comprising the selectivity filter are shown in spacefill, CPK colors, and labeled. The brown peptide cartoon on the extracellular side (red sphere layer for outer leaflet) is the µ-conotoxin KIIIA. The spacefill molecule in the pore near the blue sphere layer representing the inner leaflet is the neurotoxin veratridine (VTD), which inhibits channel inactivation and lengthens the action potential with possibly fatal consequences. A single Na+ ion is shown at the top of the pore as an orange sphere labeled Na. The µ-conotoxin blocks the pore. The Ile1488-Phe1489-Met1490 (IFM) motif, found in the intracellular linker between domain III and IV (near the cytoplasmic face of the receptor, responsible for the fast inactivation, are shown in gray spheres and labeled with single-letter codes.
The selectivity filter DEKA is different from the selectivity filter in another sodium channel (NavAb) which has 4 glutamate. Asp and Ala line the wall of the filter region and Glu and Lys can attract and release, respectively, the Na+ ion. For fast inactivation, the IFM motif must interact with an"inactivation gate receptor" within the protein itself. Likely candidates for this are short intracelllar loops connecting all the S4 and S5 segments. This receptor appears to contain 3 amino acids, F1651, L1660 and N1662.
Figure \(\PageIndex{24}\) shows another interactive iCn3D model of a ternary complex of human Nav1.2 with the beta2 regulatory subunit and conotoxin IIIA (6J8E) highlighting just the DEKA selectivity filter, the IFM motif, and its receptor inactivation gate F1651, L1660 and N1662.
Figure \(\PageIndex{24}\): Human sodium channel Nav1.2-beta2-KIIIA ternary complex highlighting just the DEKA selectivity filter and the IFM and its receptor inactivation gate F1651, L1660 and N1662 (6J8E). (Copyright; author via source). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/icn3d/share.html?tq3kXbT44GeCCUcY7
They are all shown in spacefill and labeled. Orient the molecule with the cytoplasmic domain at the top. The leaflets of the bilayer are omitted for clarity but the cytoplasmic pore inhibitor is still shown in sticks.
Figure \(\PageIndex{25}\) below shows a closeup of the bound Na+ ion.
Figure \(\PageIndex{25}\): Sodium ion in the SF of the PDB ID 6J8E Nav1.2 cryo-EM structure. The pore blocker μ-conotoxin KIIIA is not shown. Alberini et al. J. Chem. Theory Comput. 2023, 19, 10, 2953–2972. April 28, 2023. https://doi.org/10.1021/acs.jctc.2c00990. Creative Commons.
Structures of the closed state, the open state, and the inactivated state of NaV1.5 are now known. Key regions are shown in Figure \(\PageIndex{26}\) below. The open state was the hardest to solve since it closes in milliseconds to form the inactive state as described above. Mutations in the Ile-Phe-Met (IFM) motif to QQQ prevented inactivation. This would ordinarily be deleterious to an organism but in the presence of a small molecule inhibitor, propafenone, it was possible to isolate this state.
Figure \(\PageIndex{26}\): Closed, open, and inactivated conformations of the activation gate and the locations of arrhythmia mutations. Daohua Jiang, Richard Banh, Tamer M. Gamal El-Din, Lige Tonggu, Michael J. Lenaeus, Régis Pomès, Ning Zheng, William A. Catterall. Open-state structure and pore gating mechanism of the cardiac sodium channel. Cell, Volume 184, Issue 20, 2021, 5151-5162.e11, ISSN 0092-8674,. https://doi.org/10.1016/j.cell.2021.08.021. Reprinted with permission from Elsevier. May not be sublicensed, assigned, or transferred to any other person without publisher's written permission.
Panel (A) shows the closed activation gate of NaV1.5 generated by MODELER based on the resting-state structure of NaVAb (PDB: 6P6W), sealed by a square of hydrophobic side chains of hydrophobic residues V413, L941, I1471, and I1773 (spacefill, black) that in the closed state completely seal off the cytoplasmic opening in the pore. These ring of amino acid side chains come together on conformational changes resulting from the engagement of the IFM motif with its internal receptor.
Panel (B) shows the open activation gate of NaV1.5/QQQ triple mutation. Red arrows indicate the directions of movement of S6 segments compared to the resting state.
Panel (C) shows the partially open but nonconductive activation gate of rNaV1.5C in the inactivated state. Red arrows indicate the directions of movement of the S6 segments compared to the open state.
Panels (D–F) show structures from (A) to (C) are shown in space-filling surface representation with hydrated Na+ placed in the central cavity behind the activation gate. Red and green spheres represent water and Na+, respectively. van der Waals distances measured across the orifice of the activation gate are 4.3 Å (DI-DIII) × 2.8 Å (DII-DIV) for the resting/closed state, 6.9 Å (DI-DIII) × 5.0 Å (DII-DIV) for the inactivated state, and 7.3 Å (DI-DIII) × 8.2 Å (DII-DIV) for the NaV1.5/QQQ open-state structure.
Panels (G–I) show structures from (A) to (C) with the locations of arrhythmia mutations causing LQT-3 overlaid as green spheres
The spacefill models in D-E clearly show that the cytoplasmic opening is "open" in the open state E (obviously), and occluded to increasing degrees in the inactive state (F) and closed state D.
Finally, figure \(\PageIndex{27}\) shows an interactive iCn3D model of the electrostatic surface potential of the rat Nav1.5 channel (6UZ3)
Figure \(\PageIndex{27}\): Electrostatic surface potential of the rat Nav1.5 channel (6UZ3)
(Copyright; author via source). Click the image for a popup or use this external link: https://structure.ncbi.nlm.nih.gov/i...UZdQeUUPtYGgR6
The red indicates negative potential and the blue positive potential. The white is neutral. Note that the bilayer representations are essentially neutral with respect to their effect on the overall surface potential. Tilt the model to view the top and bottom entrance to the pore and the overall negative charge density expected in the net attraction of the positive Na+ ions.
Lipid-Gated Ion Channels
Membrane receptors are in the lipid bilayer, so it should not be too surprising that specific lipids might bind and trigger conformational changes in the receptor, mediating a specific biological activity. The specific lipid might form during an upstream event, then bind to the receptor, triggering function in a process of signal transduction, which we will explore in the next chapter. Let's look at receptors gated by binding of the lipid phosphatidylinositol bisphosphate (PIP2). It is found in small concentrations in membranes and can be cleaved in by phospholipase C to form a small polar intracellular signaling molecule, IP3 (discussed in Chapter 12). PIP2 can also recruit proteins to the membrane and participate in signaling events that way. For this section, we will discuss how it binds to a K+ ion channel protein and open so K+ can flow into cells (the opposite direction of the normal efflux), which helps control transmembrane potential.
Kir2.2 -Inward rectifier potassium channel Kir2.2
The names of this channel can best be understood if you understand the meaning of the word rectify. The verb has several meanings but for us, the best definition is to correct. What does this channel correct? When is it functional? We'll explore the details more in the next chapter we first a better understanding of what happens to the actual Na+ and K+ ion concentrations outside and inside the cell during neural activation. How much do they change? We need this to understand the driving force for the Kir2.2 channels that move K+ into the cell, which is opposite the usual direction. From that sense, it is "rectifying" the K+ concentrations.
When a neural cell is activated or fires, the cell membrane potential goes from a resting potential of around -60 to -70 mV (inside negative ) to a more positive potential as Na+ ions enter the cell through voltage-gated Na+ channels (after an early neurotransmitter-gated ion channel is open after ligand binding) with the ions flowing down a chemical and electric potential gradient. At a certain membrane potential (about +30 mV), K+ channels open allowing an efflux of K+, also down both a chemical and electric potential gradient, returning the cell potential close to its equilibrium value potential of around -60 to -70 mV (inside negative). But how much do the actual K+ and Na+ ion concentrations change in this process? The somewhat counterintuitive answer is hardly any at all!
We need to understand how the membrane acts as a capacitor first. The charge Q on a surface of a plate or side of a membrane is proportional to the voltage across the plate or membrane. Figure \(\PageIndex{28}\) shows how a membrane with a transmembrane potential acts as a capacitor. The dielectric medium in the capacitor will determine how quickly the charges on the plate will dissipate. When the medium is an insulator, resistant to charge flow, the plates remained charged longer. The same is true for the membrane. The hydrophobic bilayers act as an insulator and resist the discharge of the membrane potential. The bilayer offers high resistance (low conductance) to charge flow. Only when channels are open and the ions become reasonably permeable to flow does the membrane potential change over short periods. The following derivation is adapted.
It makes sense that the stored charge (Q) on either side of the membrane is proportional to the membrane voltage. We can write the following simple equations:
\begin{equation}
\begin{array}{l}
Q \propto V \\
Q=\mathrm{C} V
\end{array}
\end{equation}
where C, the proportionality constant, is the capacitance with units of the Faraday (which you remember from introductory chemistry). Let's normalize this equation for an area of 1 cm2. The measured capacitance of lipid bilayers is about 10-6F/cm2. Let's assume a voltage change from -70 mV to + 30 mV for a total of 0.1 V. Hence
\begin{equation}
Q=\frac{10^{-6} \mathrm{~F}}{\mathrm{~cm}^{2}}(0.1 \mathrm{~V})=\frac{10^{-7} \mathrm{Coul}}{\mathrm{cm}^{2}}
\end{equation}
Let's change that into the number of elementary charges on the surface of the membrane per μm2 surface area.
\begin{equation}
\left(\frac{10^{-7} \mathrm{Coul}}{1 \mathrm{~cm}^{2}}\right) x\left(\frac{1 \text { ion }}{1.6 \times 10^{-19} \mathrm{Coul}}\right)=\frac{6.25 \times 10^{11} \text { ions }}{\mathrm{cm}^{2}} \times \frac{1 \mathrm{~cm}^{2}}{10^{8} \mu \mathrm{m}^{2}}=\frac{6,250 \text { ions }}{\mu \mathrm{m}^{2}}
\end{equation}
What does this mean for an ordinary eukaryotic cell? Let's model the cell as a sphere with a diameter of 10 μm.
Knowing the equations for the volume (V = (4/3)πr3) and surface area (4πr2), the volume of 10 μm cell is about 524 μm3 and the surface area is 314 μm2. The table below shows the resting ion concentrations in a cell and the actual number of ions in the 524 μm3 volume of the cell (column 3).
Using the calculated value of 6250 ions moved/μm2, the total number of K+ and accordingly Na+ ions that move across 314 μm2 of total cell membrane surface area is about 2 million. The results are shown in Table \(\PageIndex{3}\) below.
| 1. ion | 2. [ion]intracellular (mM) | 3. # ionsintracellular | 4. total ions moved during neuron response | 5. change in [ion]intracellular |
| sodium | 10 mM | 3.2 × 109 Na+ | ~ 2,000,000 in on depolarization | ~6.3 x 10-2 mM (~0.6% change) |
| potassium | 150 mM | 4.7 × 1010 K+ | ~ 2,000,000 out on repolarization | ~6.3 x 10-2 mM (~0.6% change) |
Table \(\PageIndex{3}\): How many ions move across a membrane
\begin{equation}
\frac{2 \times 10^{6} \mathrm{Na}^{+} x\left(\frac{1 \mathrm{~mol} \mathrm{Na}^{+}}{6.022 \times 10^{23} \mathrm{Na}^{+}}\right)}{524 \mu M^{3} \times\left(\frac{1 \mathrm{~L}}{10^{15} \mu M^{3}}\right)}=6.3 \times 10^{-6} \mathrm{M}=6.3 \times 10^{-3} \mathrm{mM}
\end{equation}
The actual change in intracellular Na+ ion concentration on excitation is only about 0.6% of the initial [Na+]intracellular on excitation and depolarization of the cell. We can also assume that the K+ ion changes to the same degree in repolarization. So when the Na+ and K+ channels open, the "flood gates" are not opened. Permeability does increases, but this leads to a tiny influx of Na+ ions, which is not sufficient to change the intracellular Na+ concentration. It is, however, enough to change the transmembrane potential! It's a misconception that there are significant changes in ion concentration across the membrane on depolarization and repolarization of the cell. The Goldman-Hodgkins-Katz equation (previous section), shows that the membrane potential is a function of both concentrations and permeability coefficients.
Now we can present the inward rectifying potassium channels, which facilitate the movement of K+ into the cell from the outside. This is in the opposite direction of the usual flow of the ions. Since the ions are moving towards higher levels of K+ inside the cell, it would appear this would be an example of either passive diffusion favored only by the electrical potential or a case of active transport. None of these is true. K+ ions diffuse from outside to inside the cell since outward diffusion is substantially blocked by molecules such as polyamines and Mg2+! We don't have to invoke active transport or a violation of the basic rules of thermodynamics. The channels thus display strong inward currents and weak outwards ones.
The channels allow large conduction of K+ ions if the membrane potential is more negative compared to the resting K+ ion equilibrium potential but less if more positive, so the net effect is to maintain the resting K+ potential.
There are several subfamilies of Kir channel. They are always potentially active (open) except those gated by G-proteins (see next chapter) or by ATP binding. (these are involved in metabolism). Kir activity is regulated by phospholipids and proteins. Now we will explore the Kir 2.2 channel, which is gated-open by PIP2, a membrane lipid, not by changes in the transmembrane potential. Yet by opening this channel and allowing the inward flow of K+ ions, PIP2 is regulating the transmembrane potential. It is the agonist for the Kir 2.2 channel.
Instead of having monomeric units with S1-S6 transmembrane helical segments with a voltage sensor (S4) and P loop and S5-S6 selectivity filter, it has just 2 transmembrane helices. Both the N- and C-termini are in the cytoplasm, connected by an extracellular loop (H5) which helps form the prototypical K+ selectivity filter with the consensus sequence T-X-G-Y(F)-G. Similar to the voltage-gated K+ channel, four of these aggregate to form homo- or heterotetramers in the membrane. Figure \(\PageIndex{29}\) illustrates these points.
The proteins have large intracellular domains (ICD). On binding of PIP2 to the region between the transmembrane and ICD, which produces a large conformational change, allowing K+influx. The model below shows the R186A mutant tetrameric Kir 2.2 channel (3SPG) with four bound PIP2 analogs containing two short fatty acids (octanol) esterified to the glycerol backbone. There appear to be two binding sites for lipids, a nonspecific site in the TMD and a specific one for PIP2 in the ICD.
Figure \(\PageIndex{30}\) shows an interactive iCn3D model of the inward rectifying R186A mutant tetrameric Kir 2.2 channel (3SPG) with four bound PIP2 analogs containing two short fatty acids (octanol) esterified to the glycerol backbone. Hover over the residues to identify them.
_.png?revision=1&size=bestfit&width=216&height=333)
Figure \(\PageIndex{31}\) shows an animation that shows the monomeric Kir protein morphing from the apo state (without PIP2, 3JYC) to the PIP2 bound state (3SPI).

Another PIP2-gated ion channel is the transient receptor protein (TRP) channel. These channels play a role in vascular tone. Smooth muscle cells have TRPC3 and TRPC6 channels, Na+ or Ca2+ channels that cause depolarization, leading to smooth muscle contraction and vasoconstriction.
Mechanosensitive channels
We saw in the previous chapter that some pores (not channels) are gated open not by voltage, or specific agonists such as neurotransmitters or even specific lipids like PIP2 but by more general changes in membrane bilayers properties (membrane tension, curvature, pressure). Likewise, specific channel proteins can be gated by changes in the physical properties of the bilayer. We will consider one mechanically-active channel, TRAAK.
TRAAK - Potassium channel subfamily K member 4
The protein is a K+ ion channel that is not sensitive to voltage changes but is open on the mechanical deformation of the bilayer. The channel can be opened by making the cytoplasm basic, raising the temperature. It is involved in pain sensation and pressure transduction. The TRAAK 4 opening is blocked by the presence of lipid from the inner leaflet which occludes the pore. If the lipid is removed by physical changes, transmembrane helix 4 rotates, which prevents the lipid from blocking the channel, which opens. Further changes in the coupled transmembrane helices 2 and 3 stabilize the opening.
Figure \(\PageIndex{32}\) shows an interactive iCn3D model of the TRAAK channel protein (4wff) in the closed state. Hover over the residues to identify them.
.png?revision=1&size=bestfit&width=393&height=331)
The K+ ions are aligned in the channel. Decane, a nonpolar molecule, is shown in spacefill and colored cyan. The decane is probably decanoic acid in which the carboxyl group was not defined in the structure due to high flexibility. This suggests that the "decanoic acid" is not tightly bound. It binds through the cytoplasmic side through an opening in the membrane protein. In the open state, transmembrane helix 4 rotates, blocking access to the cavity. Hence lipid binding gates the channel closed.




.png?revision=1&size=bestfit&height=300)
.png?revision=1)
.png?revision=1&size=bestfit&width=410)