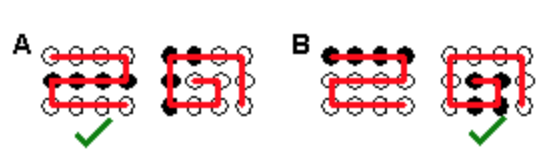Module 4.4: Tertiary Structure and Protein Stability
- Page ID
- 25243
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Understand dominant enthalpic forces that stabilize proteins.
- Understand conformational entropy.
- Understand the role of the hydrophobic effect in protein folding.
Comparison of the Folded and Denatured Forms of Proteins
Protein unfolding involves the conversion of the highly ordered native state (N), or folded (F), state to a unfolded (U), or denatured (D) state. During the unfolding process the primary structure (e.g. covalent bonds) of the protein does not change. The folded state usually has a single, well defined, and unique tertiary structure with a significant fraction of amino acids buried in the core of the protein, sequestered from the solvent. In the completely unfolded state, all amino acid sidechains will be exposed to the solvent. The denatured form of the protein is seldom biologically active while the folded or native state is usually the biologically active form of the protein.
The major differences between these two states is listed below:
| Native State | Denatured State |
|---|---|
| Compact | Larger volume |
| Single conformation | multiple conformations |
| Extensive intra-protein H-bonds | H-bonds to water |
| Many residues buried in the core | Residues exposed to solvent |
Features of the Folded State of Globular Proteins
The are a number of common characteristics of the folded state of most globular proteins. Use the following two activities to explore the contribution of secondary structure to tertiary structure and the distribution of amino acids in globular proteins.
learn by doing
1. Contribution of Secondary Structural Elements to Tertiary Structure
Answer the following questions based on the Jmol protein structure shown on the left. Use these buttons to:
- view both mainchain and sidechain atoms
- view only mainchain atoms
1. This protein contains
a. helical residues
b. sheet residues
c. both helical and sheet residues
- hint
-
highlight the helix in red and the sheet in green
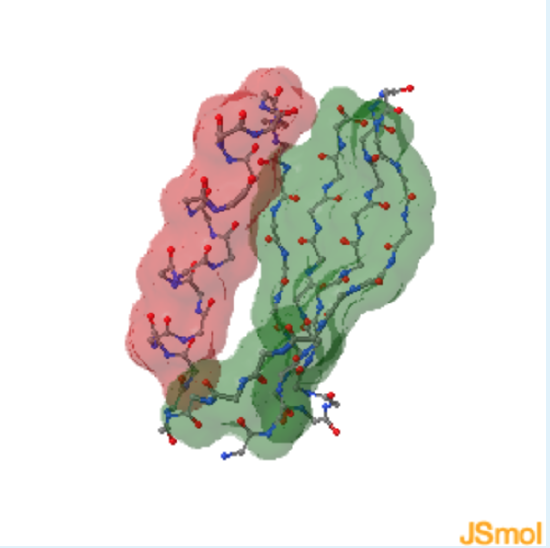
- Answer
-
c.
2. Amino Acid Distribution in Folded Globular Proteins
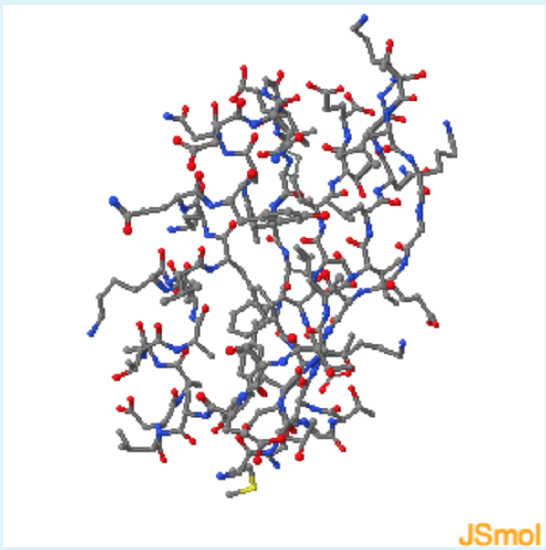
Use these checkboxes to inspect the aspects of this structure in order to answer the questions below:
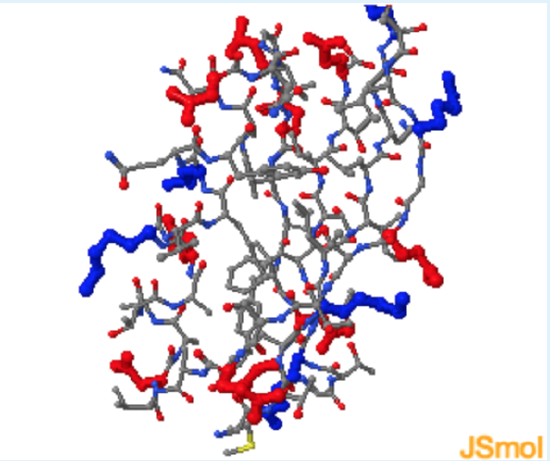
- Highlight charged res. (red=-, blue=+).
- Highlight polar residue (yellow).
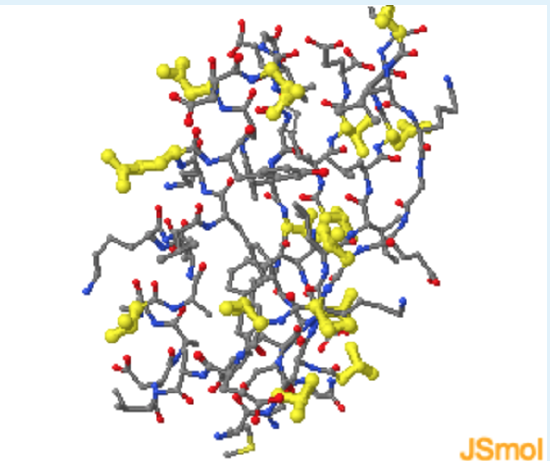
- Highlight hydrophobic residue (black)
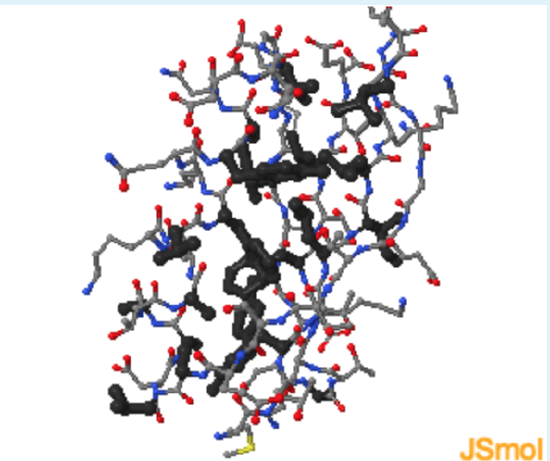
Use these checkboxes to inspect the aspects of this structure in order to answer the questions below:
Based on the protein G Jmol , which of the following is the best description for the distribution of residues in a folded globular protein?
Charged residues; Polar residues; Non-Polar residues:
a. exterior only
b. interior only
c. both exterior and interior
- hint
-
It is helpful to watch the molecule rotate to get a better sense of interior versus exterior.
- Answer
-
a (charged residues are indeed found on the surface.); a (polar residues are indeed found on the surface.); c (Non-polar residues are found on both the surface and the interior.)
Thermodynamic Factors that affect the Stability of the Native State
The properties of the folded state of a protein, a compact, highly hydrogen bonded structure with a non-polar core, can be understood by considering the energetic terms that lead to the stability of the folded state.
Proteins form a stable folded state if the standard energy difference,
\[\Delta G^{\circ}=G_U^{\circ}-G_N^{\circ}\]
between the two states is positive, indicated that the native state (N) is more stable (lower in Gibbs energy) than the unfolded (U) state. \(\Delta G\)o is the change in the energy of the system when one mole of reactant(s) are converted to one mole of product(s). The standard energy change can be related to the equilibrium position of the reaction:
\[\Delta G^{\circ}=-RT \ln K_{eq} \nonumber\]
or
\[K_eq=e^{-\Delta G/RT}\nonumber\]
A positive value for \(\Delta G\) will give an equilibrium constant that is less than one (\(e^{-x}\) < 1), another indication that the concentration of reactants (N-state) is higher than the product (U-state).
The relative stability of the folded versus the denatured depends on the environment of the protein. Environmental conditions such as high temperature, extremes of pH, or the presence of organic solvents, can cause the unfolded state to become lower in energy than the folded state. The effect of these environmental conditions on the stability of proteins can be understood by considering the factors that contribute to the stability of the native or denatured state.
Both the enthalpy and entropy contribute to the overall Gibbs energy of the system as follows:
\[\Delta G^{\circ} = \Delta H^{\circ} - T \Delta S^{\circ},\]
where \(\Delta H^{\circ}\) and \(\Delta S^{\circ}\) are the standard changes in enthalpy and entropy, respectively. The contribution of each of these terms to the stability of the folded state is discussed in the following sections.
Enthalpy (\(\Delta H\))
Enthalpy (\(\Delta H\)) is the amount of heat generated/consumed by the reaction when 1 mole of reactants are converted to one mole of products.
\[\Delta H^{\circ} = H^{\circ}_{Products} – H^{\circ}_{Reactants}\nonumber\]
The enthalpy is related to changes in molecular interactions (i.e. hydrogen bonds, van der Waals, etc.). In biochemistry, these interactions usually involve non-covalent changes. A positive enthalpy is unfavorable since it implies that bonds have been broken, (e.g. hydrogen bonds), because heat has been added to the system. Reactions that release heat (decrease in \(\Delta H\)o) are favorable, from an enthalphic point of view.
learn by doing
The \(\Delta H^{\circ}\) associated with hydrogen bonding
The \(\Delta H^{\circ}\) associated with hydrogen bonding is unfavorable for unfolding. Hydrogen bonds are more stable in the native form of the protein by about 1-2 kJ/mol. Most of the hydrogen bonding partners in the interior of the folded form of the protein form hydrogen bonds, usually by forming regular secondary structures. This occurs because the energetic cost of breaking a hydrogen bond to water (in the unfolded state) and not reforming that hydrogen bond in the folded state, is about 20 kJ/mol.
Protein G
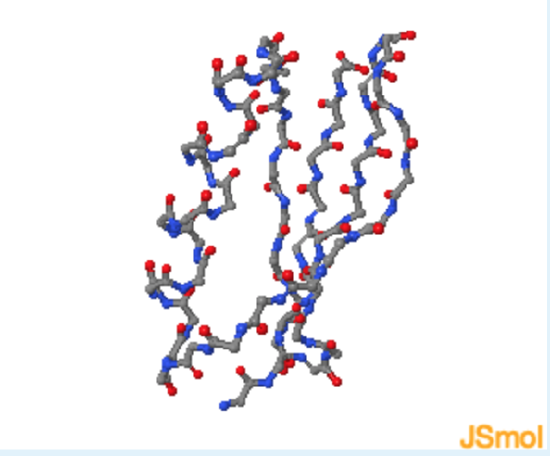
- Show mainchain H-bond
-
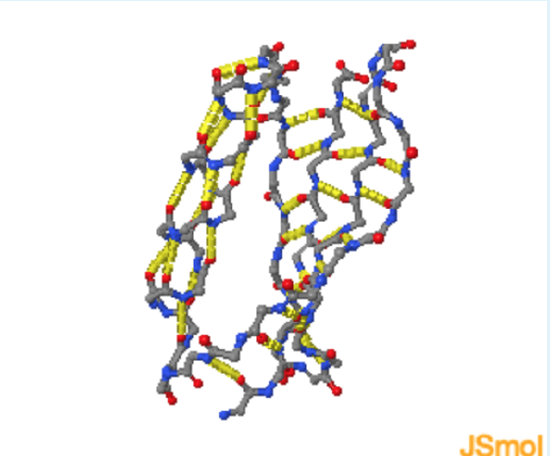
- Add sidechain H-bond
-
- Zoom in
-
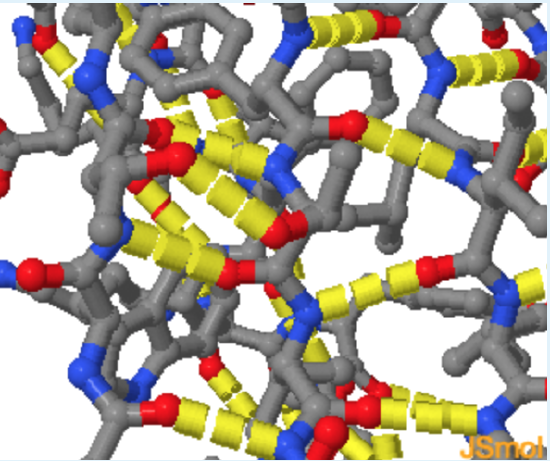
Energetics of Hydrogen Bonds
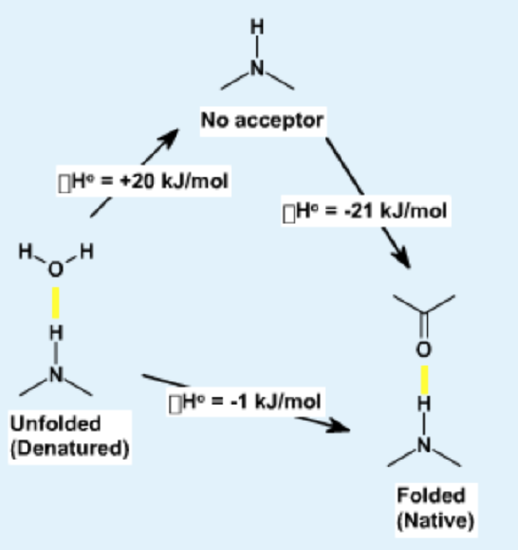
In the unfolded state (left) hydrogen bond donor and acceptors on the protein form hydrogen bonds with water. During folding, these hydrogen bonds are broken, requiring an input of energy of approximately +20 kJ/mol. The hydrogen bonds are reformed in the folded state, in this case between donors and acceptors in the protein. These hydrogen bonds are slightly more stable than those to water because of a more optimal geometry, leading to a net decrease in enthalpy.
The \(\Delta H^{\circ}\) associated with van der Waals
The \(\Delta H^{\circ}\) associated with van der Waals forces is unfavorable for unfolding. Van der Waals interactions are more stable in the native form of the protein because of the optimal surface contact between residues in the folded form.
Protein G

- Show vdw surface
-
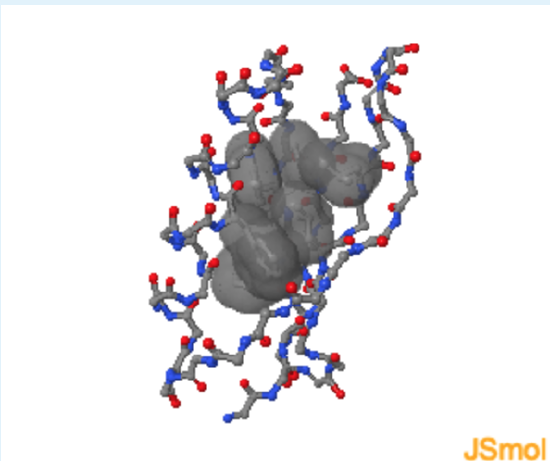
- Remove Leu 5 surface
-
Energetics of Hydrogen Bonds
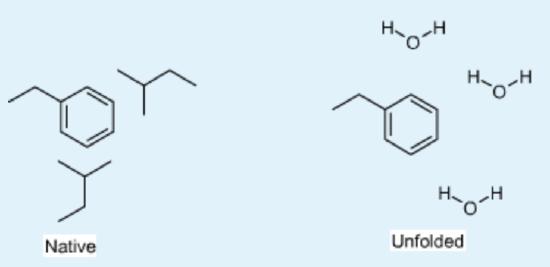
In the unfolded state (right) atoms in the Phe sidechain of a residue show weak van der Waals interactions with the solvent. After folding, the same Phe sidechain atoms are in optimal van der Waals contact with two Leu residues in the non-polar core.
Electrostatic forces: Although these forces can contribute to Δ Ho changes in many biochemical interactions, they are usually not important for protein folding because the charged residues remain on the surface and therefore interact with water equally well in both the native and the denatured state. The energetic cost of burying a single charge in the core of a protein is extremely high, largely due to desolvation of the ion during the folding process. Note that in some proteins charge-pairs are buried. These are stable because the loss of energy due to desolvation is regained by favorable electrostatic interactions in a low dielectric media.
\[E_{electrostatic}=\frac{1}{4\pi\epsilon_o}\frac{q_1q_2}{Dr}\nonumber\]
Entropy Changes in Protein Folding
\(\Delta S^{\circ}\) is the change in entropy when 1 mole of reactant(s) are converted to one mole of product(s).
\[\Delta S^{\circ} = S^{\circ}_{Products} – S^{\circ}_{Reactants}\nonumber\]
A positive entropy change is favorable since the disorder in the system is increased. A positive change in entropy leads to a decrease in \(\Delta G\)o since
\[\Delta G^{\circ} =\Delta H^{\circ} - T\Delta S^{\circ}. \nonumber\]
The entropy is related to the change in the number of possible configurations (\(W\)) of the system when the reaction occurs. The entropy can be calculated from Boltzmann’s equation:
\[S = R \ln W\nonumber\]
where \(W\) is the number of conformations, and \(R\) is the gas constant (8.31 joules/mol-deg).
Conformational entropy of proteins: When a protein unfolds the entropy of the molecule increases dramatically due to a change in the conformational freedom of the phi and psi angles of the mainchain, as well as disordering of the sidechain.
In the folded state (left) the mainchain and sidechain atoms of a Thr residue are fixed in a single conformation. In the unfolded state (right) the mainchain atoms can assume any of the three stable secondary structure conformations. Rotation about the C\(\alpha\)-C\beta\) bond generates three different conformations of the sidechain.
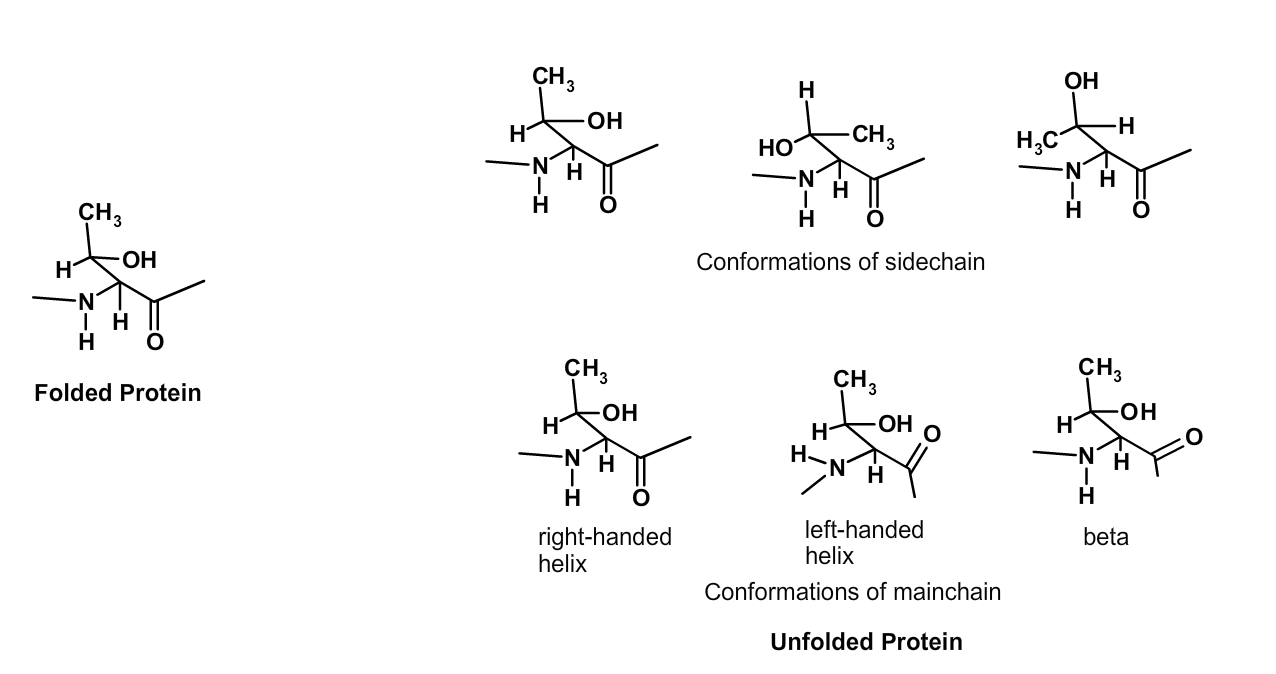
The change in the number of conformations that a residue can obtain in the unfolded state can be estimated as follows:
- There are three stable conformations of the mainchain atoms, corresponding to beta-strand, right-handed helix, and left-handed helix.
- Each rotatable bond in the sidechain can occupy three different conformations. In the case of the amino acid threonine, there are three possible side chain conformations.
- If we assume that the conformation of the mainchain atoms is independent from the sidechain atoms, then the overall number of conformations is the product of the two. In the case of threonine, W = 3 x 3 =9 conformations, at a minimum. As a rough estimate, we will assume that each reside can assume 20 different conformations in the unfolded state.
- If we assume that the conformation of one residue doesn't affect its neighbor, then the overall number of conformations for a protein that is n residues long is: \[W_1 \times W_2 \times W_3 \times ...\times W_n \nonumber.\] If we assume that each residue has ~20 conformations, the protein will have \(20^n\) different conformations.
The contribution of the enormous number of conformations to the stability of the unfolded state is enormous. For a 50 residue protein:
\[\begin{align*} \Delta S^{\circ} &=S_U−S_N\\[4pt] &=R \ln 20^{50} − R \ln 1\\[4pt] &=R 50 \ln 20\\[4pt] &=1220 \,J/mol−deg \\[5pt] \Delta G^{\circ} &=−T\Delta S^{\circ}\\[4pt] &=−300 \times 1220 J/mol \\[4pt] &=−365 KJ/mol\end{align*}\]
Hydrophobic effect - Entropy Changes of the Solvent: The hydrophobic effect is due to the entropy of the water in the system. When a non-polar side chain is exposed to water it orders, or decreases the entropy, of the water molecules. However, when the non-polar residue become buried in the non-polar center of the protein it releases all of the water which coated it. The released water can now freely diffuse in the solvent, resulting in an increase in entropy of the water. This effect is the principle reason why the cores of globular proteins are non-polar; considerable energy is released when the ordered water becomes disordered as the non-polar residues become buried in the core of the protein.
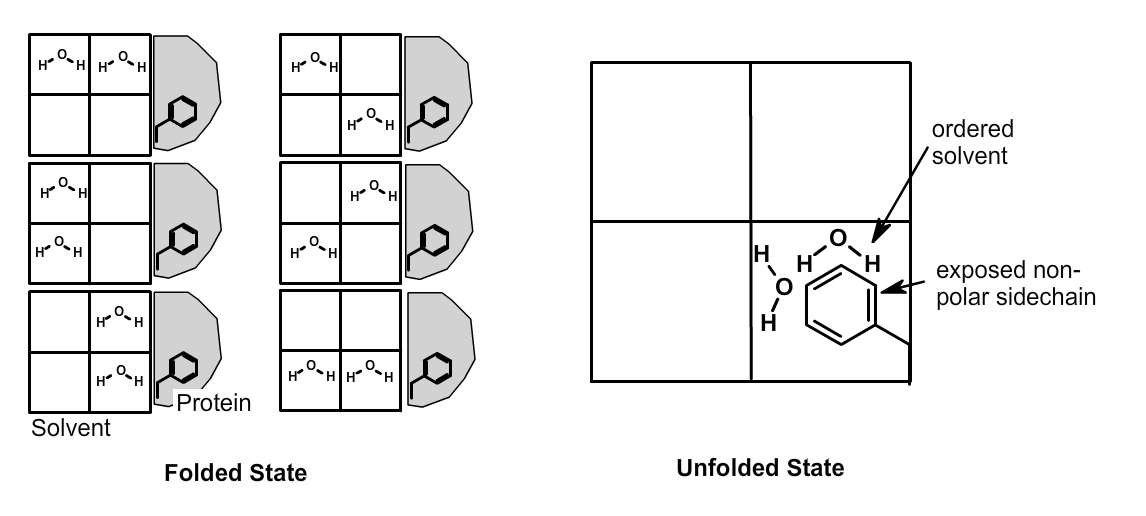
The left side of the figure shows a section of solvent, divided into four quadrants, and a folded protein with a buried Phe sidechain. Six possible distributions of the two solvent water molecules are possible when the protein is folded, i.e. \(W_{solvent}\)=6. In the unfolded state (right) the sidechain atoms of the solvated Phe residue order the two water molecules, i.e. \(W_{solvent}\)=1. During the unfolding event (left to right), the solvent becomes more ordered, which is unfavorable.
did i get this
The order of hydrophobic residues can have a large effect on the final structure of a protein. The left part of the diagram shows a 12 residue protein that contains five non-polar amino acids (black balls). It can fold into a large number of structures. Two possible ones are shown on the right, a jelly roll structure (A), or an "S" shaped structure (B). Based on your knowledge of the hydrophobic effect, which of these will be more stable?
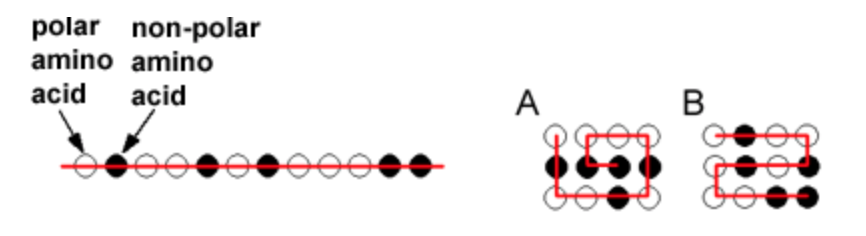
a. A
b. B
c. Both equally stable
- hint
-
The structure that buries more hydrophobic residues will be more stable.
- Answer
-
a. (only 3 hydrophobic residues are exposed in A, while four are exposed in B.)
Hydrophobicity of Amino Acid Residues: The hydrophobicity, or entropy change when a non-polar group is buried in a non-polar environment (e.g, during protein folding) depends on the non-polar surface area, as illustrated in the figure below.
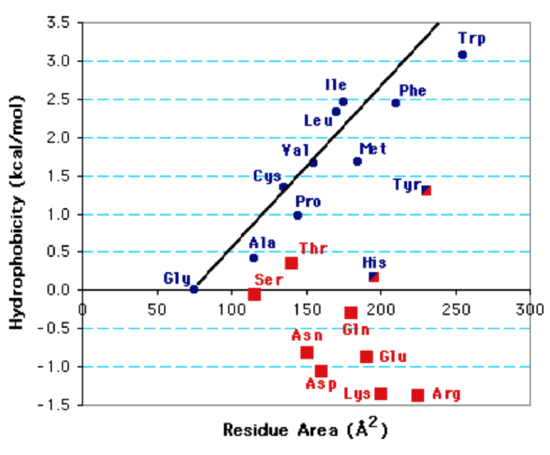
Hydrophobicity Plot: The surface area of the sidechain versus the energy required to transfer the sidechain atoms from a non-polar solvent to water (hydrophobicity) is plotted. Blue symbols represent non-polar sidechains, red symbols polar sidechains.
Overall Energetics of Protein Folding
Overall Energy Balance in Protein Folding. Protein stability is determined by the overall balance of forces that stabilize the native state and forces that destabilize it. The formation of hydrogen bonds and van der Waals interactions are favorable for folding. The hydrophobic effect also stabilizes the native state due to the non-polar nature of the core. The large conformational entropy stabilizes the denatured state. The role of each of these effects on the energy of a 50 residue protein are:
| Effect | Contribution to \(\Delta G\)o (Δ Ho, -T\(\Delta S^{\circ}\)) |
|---|---|
| Configurational entropy | - 365 KJ/mol |
| Hydrophobic effect | + 210 KJ/mol |
| van der Waals | +125 KJ/mol |
| H-bonds | +50 KJ/mol |
| Net Sum | +30 KJ/mol |
This table shows the contribution of entropy and enthalpy to the overall stability of a 50 residue protein. Entropy changes have been converted to free energy changes using \(\Delta G=-T\Delta S\). Positive values indicate that the native state is stabilized, i.e. energy is required to unfold the protein.
Summary of Structural Features & Thermodynamic Forces
There are two important features to note:
- The net stability of a protein is quite marginal.
- All three features, the hydrophobic effect, van der Waals, and H-bonds are required to overcome the very favorable change in conformational entropy when a protein unfolds. This delicate balance is illustrated in the following diagram.
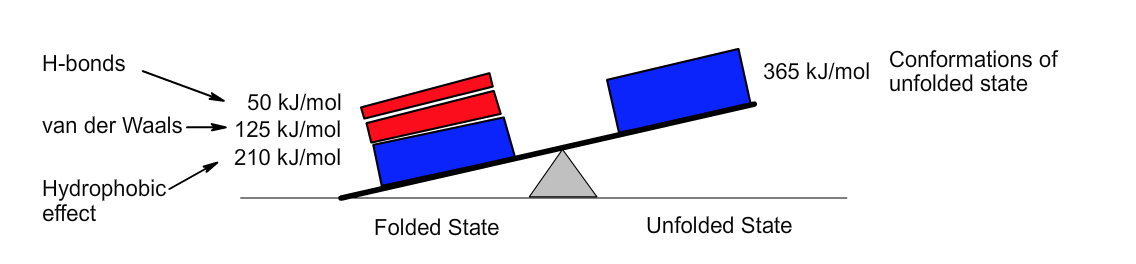
Enthalpic (red) contributions from H-bonds and van der Waals interactions, as well as entropy gains (blue) from the hydrophobic effect stabilize the native state. The increase in conformational entropy (blue) during unfolding stabilizes the unfolded state.
The following features of a folded globular protein are a consequence of the thermodynamics forces that stabilize the folded form of the protein, listed in order of significance, from left to right. Conformational entropy has been left off of this chart, remember it is very destabilizing for the folded state.
| Feature of Tertiary Structure | Hydrophobic Effect | van der Waals Interactions | H-bonds |
|---|---|---|---|
| Non-polar residues in core. | + | ||
| Well packed core. | + | ||
| Hydrogen bonded secondary structures | + |
learn by doing
Interplay between 2o structure and 3o structure.
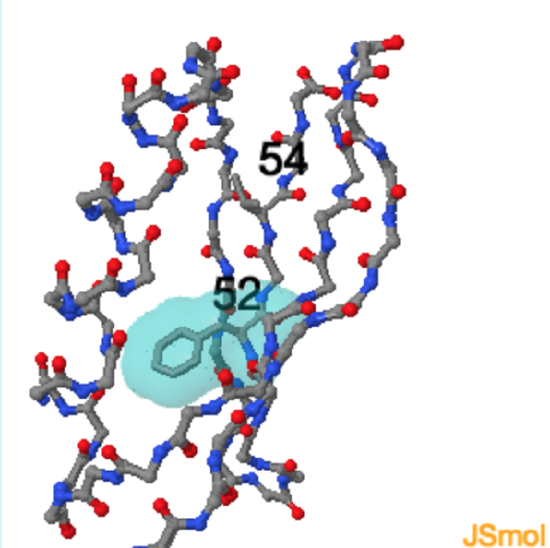
Use the Jmol protein structure to answer the following questions
Protein G
Alpha-helices and beta-sheets are equally stable from the perspective of the mainchain atoms, why is one favored over another?
- hint
-
How does the sidechain orientation differ for the two structures?
- Answer
-
The periodicity of buried non-polar residues in the sequence will determine the secondary structure. An alpha-helix will form if every 3.4 residues are non-polar, as this structure will place all non-polars on the same face of the helix.
to visualize this periodicity on the helix. A beta-strand will form if every second residue is non-polar, as this structure will place all non-polars on the same face of the sheet. to see this periodicity on one of the central beta-strands.
Review Quiz
did i get this
1. The unfolding of regular secondary structure causes
a. little increase in the entropy of protein.
b. large decrease in the entropy of the protein.
c. no change in the entropy of the protein.
d. large increase in the entropy of the protein.
e. little decrease in the entropy of the protein.
- hint
-
Does the protein chain become more disordered when the protein unfolds? What is the relationship between disorder and entropy?
- Answer
-
d. (The number of possible conformations of each residue in the unfolded form is considerably higher than in the folded form, leading to large changes in entropy.)
2. Which of the following 'forces' is the most favorable for protein folding?
a. Conformational Entropy.
b. Hydrophobic Interactions.
c. Van der Waals Interactions.
d. Hydrogen Bonds
e. Electrostatic interactions
- hint
-
Which force seems to tip the balance towards the folded state?
- Answer
-
b. (The release of water that occurs when non-polar residues are buried in the protein causes a large favorable (positive) change in entropy.)
3. wo proteins (A,B) that have the same composition (four non-polar residues) but different sequences fold into an arrangement of 4x3 atoms (right diagram).
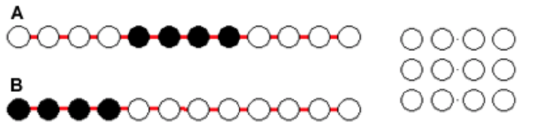
In their most stable state protein A will fold into an _____; while protein B will fold into a ______
a. S-shape
b. Jellyroll shape
- hint
-
A: Pick the structure that buries more hydrophobic residues.
B: Since the sequences are different, the structures are likely different.
- Answer
-
a; b