Module 4.3: Secondary Structure

Last updated
Save as PDF

Page ID: 24754

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Understand consequences of orbital overlap on the configuration of the peptide bond.
Understand why trans peptide bonds are more stable.
Understand geometrical properties of linear polymers.
Understand the role of hydrogen bonds in the stability of secondary structures.
Predict the secondary structure of a residue from the Ramachandran plot

Conformational Geometry of Peptides and Proteins:

Before discussing secondary structure, it is important to appreciate the conformational plasticity of proteins. Each residue in a polypeptide has three bonds connecting mainchain atoms that are potentially free to rotate. The conformation of the atoms involved in these bonds describes the secondary structure of the protein. The rotation angle about a bond is referred to as a torsional angle. A torsional angle defines the relative orientation of four atoms in space and it is the angle between two planes. The torsional angle between the N and C\(\alpha\) bond is shown below.

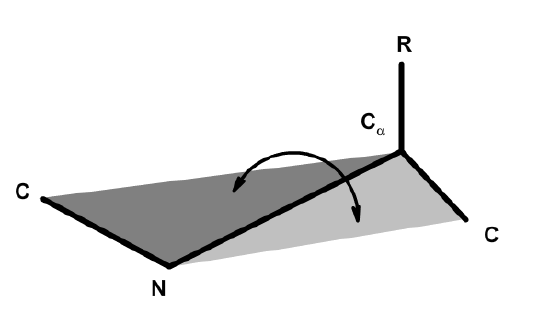
Screen Shot 2019-07-18 at 11.18.56 PM.png

The torsional angle about the N-C\(\alpha\) bond is defined by the angle between the two intersecting planes.

Conformation of the \(C_{i-1}\)- N (Peptide bond). The four atoms that make up this bond are planar due to the hybridization properties of the carbonyl carbon and the nitrogen (both \(sp^2\)). In addition, free rotation about the bond is not possible since the \(p_z\) orbitals of oxygen, carbon, and nitrogen form a delocalized system. Rotation about the peptide bond would break the interaction between the \(p_z\) orbital of the nitrogen and carbon atoms, and is therefore unfavorable. The peptide bond is said to be a "partial double bond".

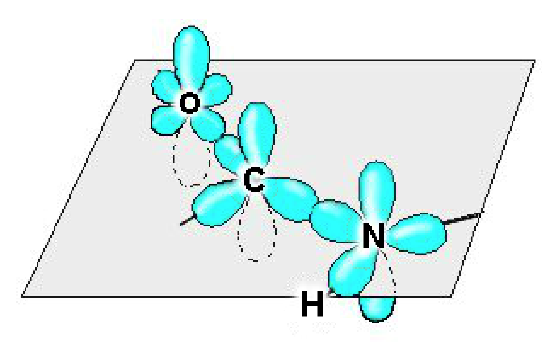
Screen Shot 2019-07-18 at 11.43.15 PM.png

The atomic orbitals of the mainchain atoms are shown. The carbonyl carbon uses an \(sp^2\) hybrid orbital to bond to the carbonyl oxygen and the nitrogen. Consequently, the oxygen, carbon, and nitrogen all lie in the same plane. Since the nitrogen is also uses \(sp^2\) hybrid orbitals, the amide hydrogen is also on the same plane. The second bond between the carbonyl carbon and oxygen is formed by overlap of the \(p_z\) orbitals. The nitrogen \(p_z\) orbital is also in a favorable position to overlap with the carbon \(p_z\) orbital. Consequently, the electrons in all three \(p_z\) orbitals form a delocalized system resulting in a partial double bond between the carbonyl carbon and the nitrogen.

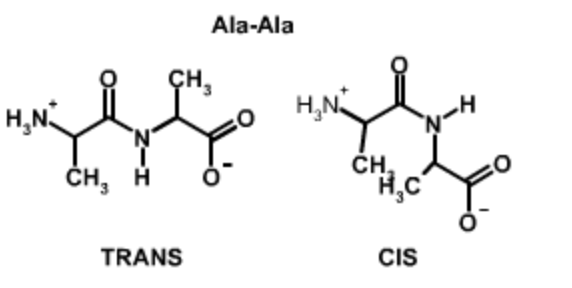
Cis and Trans Peptide Bonds: Two possible orientations of the peptide bond that maintain a favorable \(p_z\)interaction between the carbon and nitrogen are possible. They are related by a 180\(^{\circ}\) flip of the peptide bond, generating the trans form and the cis form. For all peptide bonds, the trans form is more stable than the cis form. The higher energy of the cis form is due, in part, to overlap between the \(\alpha\)-protons on adjacent residues (non-proline) or between \(\alpha\) and \(\delta\) protons in the case of proline. Use the buttons on the Jmol images below to highlight these overlaps.

Ala-Ala Trans and Cis Peptide Bonds

Screen Shot 2019-07-19 at 4.41.05 PM.png

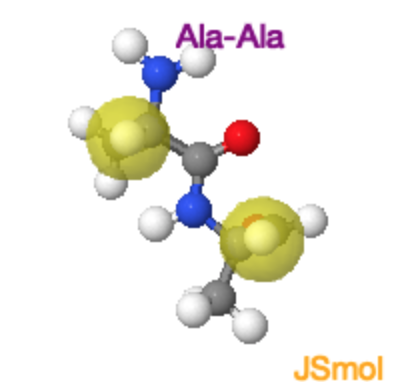
In the case of linkages between non-proline residues, the unfavorable overlap of the mainchain (and sidechain) atoms makes the cis form less stable by about 15 kJ/mol, giving a ratio of trans to cis of 1000:1. The molecular crowding of the \(\alpha\)-hydrogens in the cis form is evident in the Jmol image on the far right.

Ala-Ala Trans

Screen Shot 2019-07-19 at 4.41.15 PM.png

Screen Shot 2019-07-19 at 4.41.23 PM.png

Ala-Ala Cis

Screen Shot 2019-07-19 at 4.41.30 PM.png

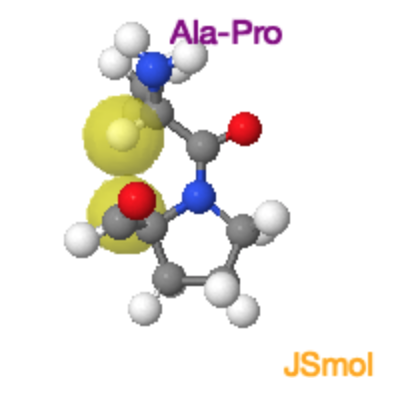
Screen Shot 2019-07-19 at 4.42.19 PM.png

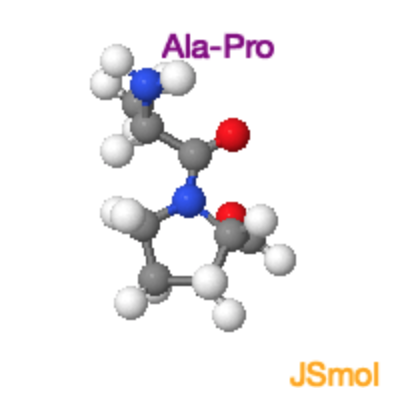
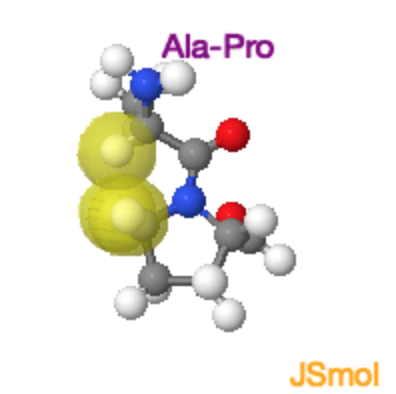
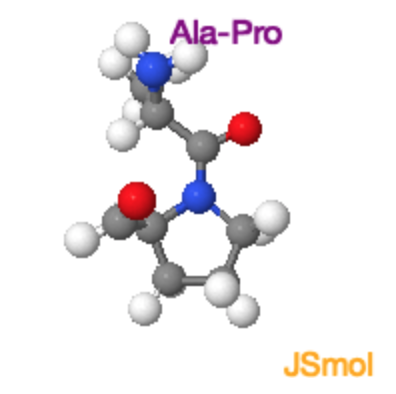
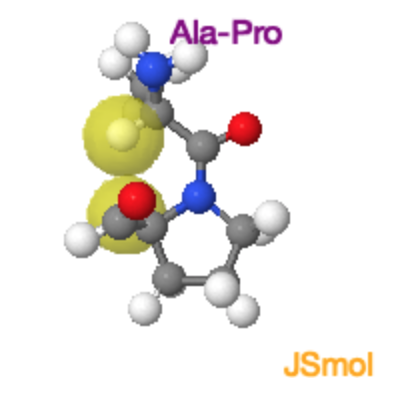
Ala-Pro Trans and Cis Peptide Bonds

Screen Shot 2019-07-19 at 4.41.56 PM.png

Both the trans and cis form of the peptide bond result in overlap of atoms, raising the energy of the trans such that it is only ~4 kJ/mol lower than the cis form. In the trans form the molecular crowding involves the \(\alpha\)-hydrogen of the preceding residue and the δ-hydrogens on the proline. In the cis form it is the two \(\alpha\)-hydrogens.

Ala-Pro Trans

Screen Shot 2019-07-19 at 4.42.06 PM.png

Screen Shot 2019-07-19 at 4.42.10 PM.png

Ala-Pro Cis

Screen Shot 2019-07-19 at 4.42.15 PM.png

Screen Shot 2019-07-19 at 4.42.19 PM.png

N - C\(\alpha\) & C\(\alpha\) - C Bonds: The torsional angles associated with each of these bonds are defined as:

\(\Phi\) (Phi), the bond between N and C\(\alpha\)

\(\Psi\) (Psi), the bond between C\(\alpha\) and C.

There is free rotation about both of these bonds. Not all torsional angles are equally likely. There are three torsional angles that are more stable than others. They are related to each other by a 120\(^{\circ}\) rotation about the bond. The three stable positions are more easily seen with a simpler molecule, such as 1-chloro-1-fluoroethane. Note that the three stable conformations minimize the interaction between the atoms on each carbon by maximizing their distance from each other. These conformations are also stabilized by favorable interactions between the molecular orbitals in the molecule.

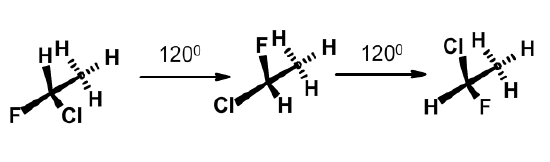
Screen Shot 2019-07-20 at 12.59.19 PM.png

In the case of amino acid residues in a protein, the presence of the bulky atoms on the sidechain restricts the possible phi and psi angles of a residue to 3 pairs of values that are relatively low in energy:

Three possible phi psi angles of a residue

\(\Phi\)=-60\(^{\circ}\), and \(\Psi\)=-45\(^{\circ}\)

\(\Phi\)=+60\(^{\circ}\), and \(\Psi\)=+45\(^{\circ}\)

\(\Phi\)=-120\(^{\circ}\), and \(\Psi\)=125\(^{\circ}\)

Secondary Structures

Proteins consist of a linear chain of amino acids, with each amino acid representing a build block. The shape of each block depends on the \(\Phi\) and \(\Psi\) angle of each residue. In regular secondary structures these angles are the same for each residue, and thus the shape of each building block, or amino acid, is the same.

If a series of identically shaped objects are laid end-to-end they will form some type of geometrical structure. In two dimensions there are two possibilities, either a straight chain or some type of circle (which may or may not be closed). A straight chain occurs if the is no curvature in the block, while a circle will result if there is any degree of curvature. The radius of the circle is related to the degree of curvature.

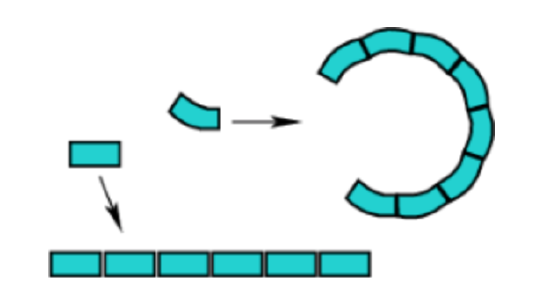
Screen Shot 2019-07-20 at 1.00.15 PM.png

In the case of three dimensional building blocks that have some degree of curvature on both faces, the two dimensional circular structure becomes a helix. If the building block is a perfect rectangular prism, then the structure will remain linear.

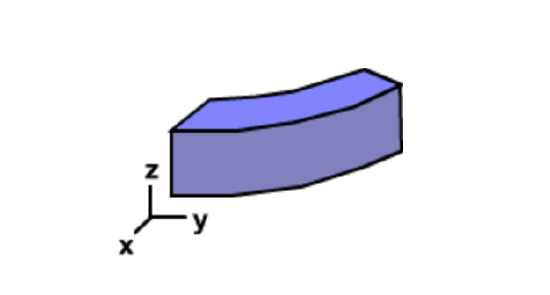
Screen Shot 2019-07-20 at 1.00.20 PM.png

Given the possible values of \(\Phi\) and \(\Psi\) angles, many different shapes of the amino acid building block are possible and therefore many different three dimensional structures are possible. Only two are commonly observed in proteins, the right-handed alpha helix and beta-structures. A left-handed alpha helix is also stable, but relatively rare . These conformations are stable because they:

Maximize mainchain hydrogen bonding
Maximize van der Waals interactions of mainchain atoms.
Minimizing steric clashes of mainchain and sidechain atoms

In all cases these secondary structures of proteins have characteristic values of the \(\Psi\) and \(\Phi\) torsional angles that are the same for each residue within a particular secondary structure. In all cases each peptide bond is rigid and planar in the trans conformation.

Alpha helix (\(\Phi\)=-60\(^{\circ}\), and\(\Psi\)=-45\(^{\circ}\))

learn by doing

Dimensions, geometry, & H-bonds:
- 3.6 residues/turn
- pitch = 5.4 A/turn
- rise/residue = 1.5 A
H-bonds || to helix axis.
Sidechains point outwards
Right handed form is more stable

\(\alpha\)-Helix

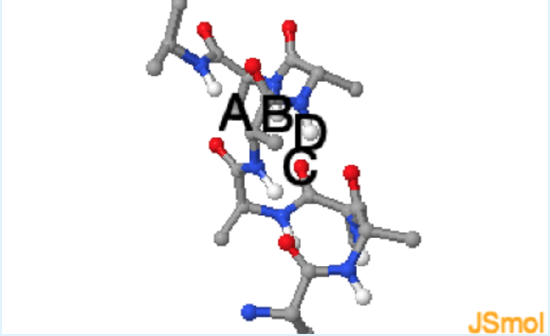
Screen Shot 2019-07-20 at 1.02.19 PM.png

Use the above Jmol to answer these questions.

1. In the Jmol image of the alpha-helix, which of the following pairs of atoms participate in a hydrogen bond?

a. A and B

b. A and C

c. B and C

d. D and C

hint: Which of the labeled atoms can be hydrogen bond donors and which can be acceptors? See donors (grey). See acceptors (orange).
Answer: c.

2. In the alpha-helix, the sidechains are found in the center of the helix, just as you would find in DNA.

a. True

b. False

hint

to color the beta-carbon of each residue cyan and look down the helix axis.

Screen Shot 2019-07-20 at 1.08.01 PM.png

Answer: b.

Beta Structures (\(\Phi\)=-120\(^{\circ}\), and \(\Psi\)=125\(^{\circ}\))

learn by doing

These particular phi and psi torsional angles generate a building block that is almost a perfect rectangular prism. Consequently, beta structures consist of straight, fully extended, strands of linked amino acids which are called beta-strands.. Due to the extended nature of the polypeptide it is not possible to form mainchain hydrogen bonds between adjacent residues. Consequently H-bonds are between adjacent strands and perpendicular to the direction of the strand. Two or more beta-strands make a beta-sheet.

\(\beta\)-Sheet

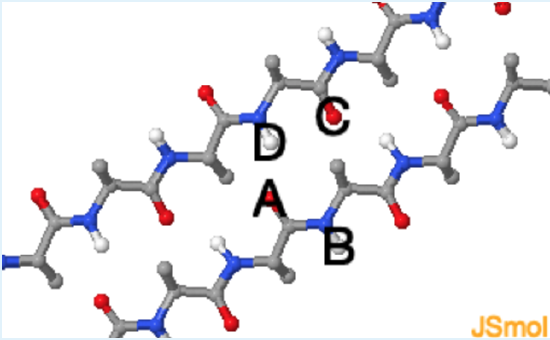
Screen Shot 2019-07-20 at 2.01.35 PM.png

The amino acid sidechains are also directed outward from the strand and alternate between pointing upwards and downwards with respect to the plane of the sheet.

Use this Jmol structure to answer the questions.

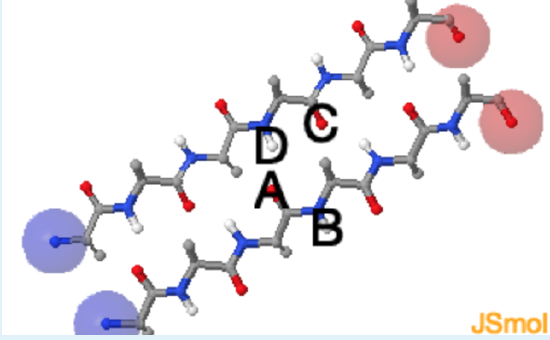
1. In the Jmol image of the beta sheet, which of the following pairs of atoms participate in a hydrogen bond?

a. A and B

b. B and C

c. A and D

d. D and C

hint: Which of the labeled atoms can be hydrogen bond donors and which can be acceptors? See donors (grey). See acceptors (orange).
Answer: c. (a. Although both atoms are of the correct type, the electropositive proton is not close to the electronegative acceptor; b. Although both atoms are of the correct type, the electropositive proton is not close to the electronegative acceptor; Although both atoms are of the correct type, the geometry is incorrect - hydrogen bonds are linear.)

2. Is the beta-sheet parallel or anti-parallel?

a. parallel

b. anti-parallel

hint

to highlight the amino-terminus and the carboxy-terminus of each strand.

Screen Shot 2019-07-20 at 2.06.02 PM.png

Answer

a. (both strands run in the same direction.)

3. In a beta-sheet, the sidechains are found in the plane of the sheet.

a. True

b. False

hint

to color the beta-carbon of each residue cyan.

Screen Shot 2019-07-20 at 2.07.37 PM.png

Answer

b. (They project from the sheet.)

In a beta-sheet there are two possibilities for the relative orientation of the individual strands. The strands can run in the same direction, generating a parallel beta-sheet, or they can run in opposite directions, generating an anti-parallel beta sheet. In both types of sheet, the beta-strands are parallel to each other.

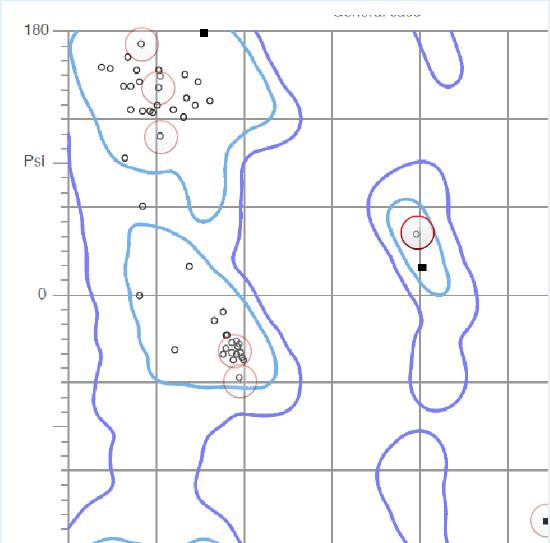
Ramachandran Plots

The phi and psi angles for each residue in a protein are neatly summarized in a Ramachandran plot. The horizontal and vertical axis represent the phi and psi angles of a peptide residue. A single point in the plot represents the phi and psi values of one residue. The contour lines surround regions of low energy and correspond to β-strand, \(\alpha_R\) helix, or \(\alpha_L\) helix secondary structures. High energy regions result from unfavorable van der Waals interactions between sidechain atoms.

learn by doing

Click on the highlighted regions of the plot to show the residues in the structure. Complete the exercise to identify which regions of the plot correspond to which secondary structure.

Screen Shot 2019-07-20 at 2.34.50 PM.png

Screen Shot 2019-07-20 at 3.37.11 PM.png

Ramachandran Plot

Screen Shot 2019-07-20 at 3.38.56 PM.png

1. Based on the blue contour lines, which area of this Ramachandran plot corresponds to high (unfavorable) energy?

a. 1

b. 2

c. 3

d. 4

hint: The symbols mark the phi and psi angles of each residue in the protein. Remember that proteins fold to assume a low energy state.
Answer: d. (Any area within the blue contour lines is low in energy.)

2. The secondary structure of region 1 corresponds to ___, region 2 corresponds to _______ , while region 3 corresponds of________.

Screen Shot 2019-07-20 at 3.45.52 PM.png

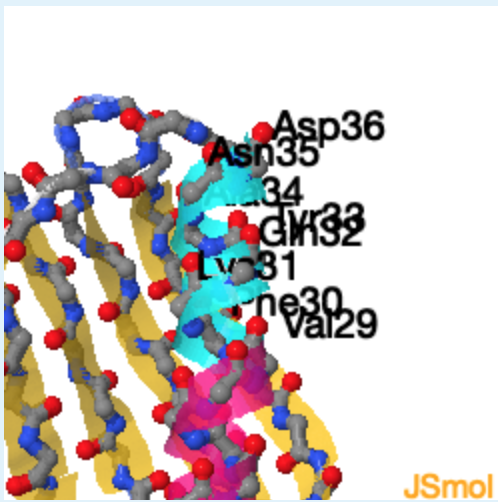
Screen Shot 2019-07-20 at 3.46.06 PM.png

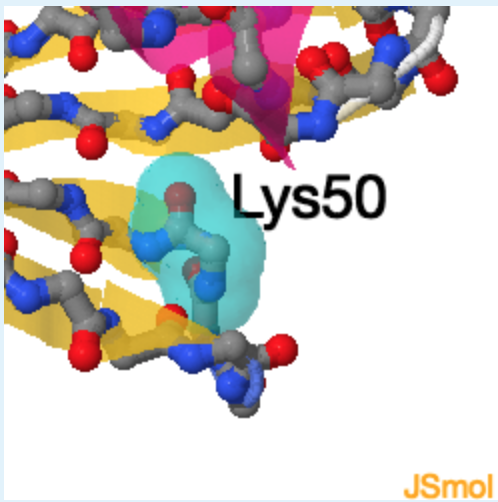
Screen Shot 2019-07-20 at 3.46.13 PM.png

a. beta-strand

b. left-handed helix

c. right-handed helix

d. unstructured

hint: check on the circled symbols in the Ramachandran plot on the lecture page to view the secondary structure in the Jmol image.
Answer: a, c, b

3. The residue indicated by 4 is found in a high energy area because it is a

a. Alanine

b. Glycine

c. Proline

d. Cysteine

e. Phenylalanine

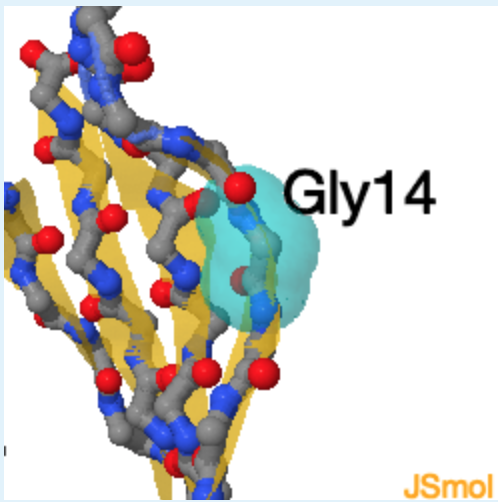
Screen Shot 2019-07-20 at 3.46.18 PM.png

hint: Click on the circled symbol in the Ramachandran plot on the lecture page to identify the residue in the Jmol image.
Answer: b. (this residue does not have a beta carbon, which allows it to assume phi and psi angles that would be high in energy for any other residue.)

Non-regular secondary structures

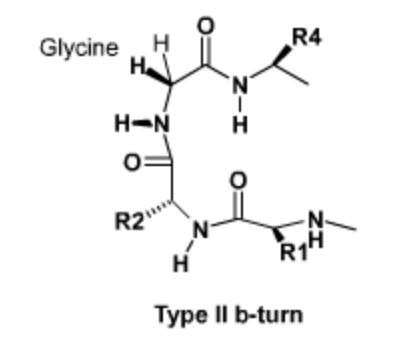
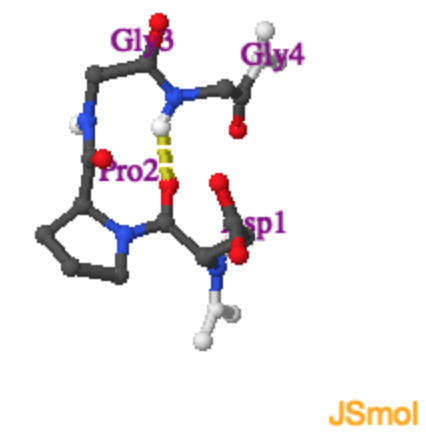
Sharp turns in proteins, particularly at the ends of beta-strands and beta-hairpins, have a characteristic geometry and sequence. As with other forms of secondary structure, these turns are stabilized by hydrogen bonding and favorable van der waals interactions. These turns often contain Glycine at position 3 (R3), because of its unique conformational properties. Use the Jmol activity to the right to determine the hydrogen bonding pattern in a type II turn.

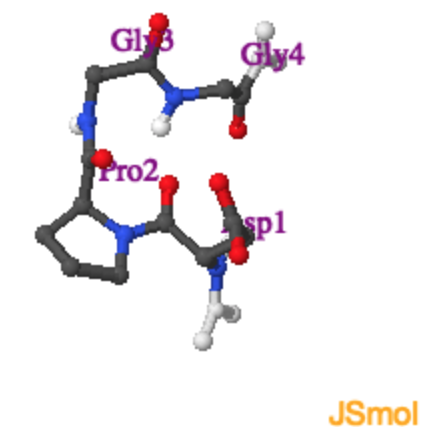
Type II Turn.

Screen Shot 2019-07-20 at 3.56.56 PM.png

Tight turns are found at the end of beta-strands. The Jmol on the right shows a type II turn with the sequence \(Asp-Pro-Gly-Gly\).

Type II Turn.

Screen Shot 2019-07-20 at 3.57.42 PM.png

Screen Shot 2019-07-20 at 3.57.49 PM.png

With hydrogen bond

Review Quiz

did i get this

1. The peptide bond in proteins is

a. planar, but rotates to three preferred torsional angles.

b. nonpolar, but rotates to three preferred torsional angles.

c. nonpolar, and fixed in a trans conformation.

d. planar, and usually found in a trans conformation.

e. not cleaved by hydrolysis.

hint: The peptide bond has partial double bond character - is there free rotation about double bonds?
Answer: d. (the atoms in the peptide bond are polar, and the bond is found in only two stable torsional angles, cis and trans. Since water is released during peptide bond formation, the reverse reaction - the addition of water (hydrolysis) can occur.)

2. Hydrogen bonds in α-helices are

a. more numerous than Van der Waals interactions.

b. not present at Phe residues.

c. analogous to the steps in a spiral staircase.

d. roughly parallel to the helix axis.

e. about 5A in length.

hint: It may be helpful to imagin the hydrogen bonding pattern in a helix.
Answer: d. (a, Nothing is more numerous in proteins than van der Waals interactions! b, All residues can form H-bonds. c, H-bonds are not found within the spiral of the helix. e, H-bonds are about 3A in length.)

3. In the alpha-helix, the sidechains are found in the center of the helix, just as you would find in DNA.

a. True

b. False

hint: The answer to this question can be found by working through the Jmol exercise on this page.
Answer: b. (this residue does not have a beta carbon, which allows it to assume phi and psi angles that would be high in energy for any other residue.)

4. If the \(\Phi\) and \(\Psi\) angles of each peptide unit in a protein are known, the following will also be determined.

a. complete secondary structure.

b. complete tertiary structure.

c. complete quaternary structure.

d. thermodynamic stability.

e. Both the first and the second choices are correct.

hint: Do the phi and psi angles refer to torsional angles on the mainchain or sidechains?
Answer: a. (Only the secondary structure is determined, i.e. the conformation of the mainchain or backbone.b, These angles only give information regarding the mainchain. Tertiary structure includes the positions of all of the side chains. c, Side chains play an important role in the quarternary structure. d, )