W2017_Lecture_03_reading
- Page ID
- 7257
Functional Groups
A functional group is a specific group of atoms within a molecule that is responsible for a characteristic of that molecule. Many biologically active molecules contain one or more functional groups. In Bis2a we will review the major functional groups found in biological molecules. These include: Hydroxyl, Methyl, Carboxyl, Carbonyl, Amino and Phosphate.

The functional groups shown here are found in many different biological molecules. "R" represents any other atom or extension of the molecule.
Attribution: Marc T. Facciotti (own work adapted from previous image of unknown source)
A functional group may participate in a variety of chemical reactions. Some of the important functional groups in biological molecules are shown above; they include: hydroxyl, methyl, carbonyl, carboxyl, amino, phosphate, and sulfhydryl. These groups play an important role in the formation of molecules like DNA, proteins, carbohydrates, and lipids. Functional groups can sometimes be classified as having polar or non-polar properties depending on their atomic composition and organization. The term polar describes something that has a property that is not symmetric about it - it can have different poles (more or less of something at different places). In the case of bonds and molecules, the property we care about is usually the distribution of electrons and therefore electric charge between the atoms. A nonpolar bond or molecule electrons and charge will be relatively evenly distributed. In a polar bond or molecule, electrons will tend to be more concentrated in some areas than others. An example of a nonpolar group is the methane molecule (see discussion in Bond Types Chapter for more detail). Among the polar functional groups is the carboxyl group found in amino acids, some amino acid side chains, and the fatty acids that form triglycerides and phospholipids.
Non-Polar Functional Groups
Methyl R-CH3
The methyl group is the only non-polar functional group in our class list above. The methyl group consists of a carbon atom bound to 3 hydrogen atoms. In this class we will treat these C-H bonds as effectively nonpolar covalent bonds (more on this in the Bond Types chapter). This means that methyl groups are unable to form hydrogen bonds and will not interact with polar compounds such as water.
The methyl groups highlighted above are found in a variety of biologically relevant compounds. In some cases, the compound can have a methyl group but still be a polar compound overall due to the presence of other functional groups with polar properties (see Polar Functional Groups discussed below).
As we learn more about other functional groups, we will add to the list of non-polar functional groups. Stay alert!
Polar Functional Groups
Hydroxyl R-OH
A hydroxyl (alcohol group) is an –OH group covalently bonded to a carbon atom. The oxygen atom is much more electronegative than either the hydrogen or the carbon, which will cause the electrons in the covalent bonds to spend more time around the oxygen than around the C or H. Therefore, the O-H and O-C bonds in the hydroxyl group will be polar covalent bonds. The figure below depict the partial charges δ+ and δ- associated with hydroxyl group.
The hydroxyl functional groups can form hydrogen bonds, shown as a dotted line. The hydrogen bond will form between the δ- of the oxygen atom and a δ+ of the hydrogen atom. Dipoles shown in blue arrows.
Attribution: Marc T. Facciotti (original work)
Hydroxyl groups are very common in biological molecules. Hydroxyl groups appear on carbohydrates (A), on some amino acids (B), and on nucleic acids (C). Can you find any hydroxyl groups in the phospholipid in (D)?
Hydroxyl groups appear on carbohydrates (A glucose), on some amino acids (B Serine), and on nucleotides (C Adenosine triphosphate). D is a phospholipid.
Carboxyl R-COOH
Carboxylic acid is a combination of a carbonyl group and a hydroxyl group attached to the same carbon, resulting in new characteristics. The carboxyl group can ionize, which means it can act as an acid and release the hydrogen atom from the hydroxyl group as a free proton (H+). This results in a delocalized negative charge on the remaining oxygen atoms. Carboxyl groups can switch back and forth between protonated (R-COOH) and deprotonated (R-COO-) states depending on the pH of the solution.
The carboxyl group is very versatile. In its protonated state, it can form hydrogen bonds with other polar compounds. In its deprotonated sates, it can for ionic bonds with other positively charged compounds. This will have several biological consequences that will be explored more when we discuss enzymes.
Can you identify all the carboxyl groups on the macromolecules shown above?
Amino R-NH3
The amino group consists of a nitrogen atom attached by single bonds to hydrogen atoms. An organic compound that contains an amino group is called an amine. Like oxygen, nitrogen is also more electronegative than both carbon and hydrogen which results in the amino group displaying some polar character.
Amino groups can also act as bases, which means that the nitrogen atom can bond to a fourth hydrogen atom as shown in the image below. Once this occurs, the nitrogen atom gains a positive charge and can now participate in ionic bonds.
The amine functional group can exist in a deprotonated or protonated state. When protonated the nitrogen atom is bound to three hydrogen atoms and has a positive charge. The deprotonated form of this group is neutral.
Attribution: Created Erin Easlon (Own work)
Phosphate R-PO4-
A phosphate group is an phosphorus atom covalently bound to 4 oxygen atoms and contains one P=O bond and three P-O− bonds. The oxygen atoms are more electronegative than the phosphorous atom resulting in polar covalent bonds. Therefore these oxygen atoms are able to form hydrogen bonds with nearby hydrogen atoms that also have a δ+(hydrogen atoms bound to another electronegative atom). Phosphate groups also contain a negative charge and can participate in ionic bonds.
Phosphate groups are common in nucleic acids and on phospholipids (the term "phospho" referring to the phosphate group on the lipid). Below are images of a nucleotide monphosphate(A) and a phosphoserine (B).
Water
Water is a unique substance whose special properties are intimately tied to the processes of life. Life originally evolved in a watery environment, and most of an organism’s cellular chemistry and metabolism occur inside the water-solvated contents of the cell. Water solvates or "wets" the cell and the molecules in it, plays a key role as reactant or product in innumerable number of biochemical reactions, and mediates the interactions between molecules in and out of the cell. Many of water’s important properties derive from the molecule's polar nature which can be tracked down to the polar molecules whose dipole originates from its polar covalent bonds between hydrogen and oxygen.
In Bis2a, the ubiquitous role of water in nearly all biological processes is easy to overlook by getting caught up in the details of specific processes, proteins, the roles of nucleic acids, and in your excitement for molecular machines (it'll happen). It turns out, however, that water plays key roles in all of those processes and we will need to continuously stay aware of the role that water is playing if we are to develop a more functional understanding. Be on the lookout and also pay attention when your instructor points this out.
In a liquid state, individual water molecule interact with one another through a network of dynamic hydrogen bonds that are being constantly forming and breaking. Water also interacts with other molecules that have charged functional groups and/or functional groups with hydrogen bond donors or acceptors. A substance with sufficient polar or charged character may dissolve or be highly miscible in water is referred to as being hydrophilic (hydro- = “water”; -philic = “loving”). By contrast, molecules with more non-polar character such as oils and fats do not interact well with water and separate from it rather than dissolve in it, as we see in salad dressings containing oil and vinegar (an acidic water solution). These nonpolar compounds are called hydrophobic (hydro- = “water”; -phobic = “fearing”). We will consider the some of the energetic components of these types of reactions in other another chapter.
In a liquid state water forms a dynamic network of hydrogen bonds between individual molecules. Shown are one donor-acceptor pair.
Attribution: Marc T. Facciotti (original work)
Water's Solvent Properties
Since water is a polar molecule with slightly positive and slightly negative charges, ions and polar molecules can readily dissolve in it. Therefore, water is referred to as a solvent, a substance capable of dissolving other polar molecules and ionic compounds. The charges associated with these molecules will form hydrogen bonds with water, surrounding the particle with water molecules. This is referred to as a sphere of hydration, or a hydration shell and serves to keep the particles separated or dispersed in the water.
When ionic compounds are added to water, the individual ions interact with the polar regions of the water molecules and the ionic bonds are likely disrupted in the process called dissociation. Dissociation occurs when atoms or groups of atoms break off from molecules and form ions. Consider table salt (NaCl, or sodium chloride). Dry a block of NaCl is held together by ionic bonds and it is difficult to dissociate. When NaCl crystals are added to water, however, the molecules of NaCl dissociate into Na+ and Cl– ions, and spheres of hydration form around the ions. The positively charged sodium ion is surrounded by the partially negative charge of the water molecule’s oxygen. The negatively charged chloride ion is surrounded by the partially positive charge of the hydrogen on the water molecule. One may imagine a model in which the ionic bonds in the crystal are "traded" for many smaller scale ionic bonds with the polar groups on water molecules.
When table salt (NaCl) is mixed in water, spheres of hydration are formed around the ions. This figure depicts a sodium ion (dark blue sphere) and a chloride ion (light blue sphere) solvated in a "sea" of water. Note how the dipoles of the water molecules surrounding the ions are aligned such that complementary charges/partial charges are associating with one another (i.e. the partial positive charges on the water molecules align with the negative chloride ion whereas the partial negative charges on the oxygen of water align with the positively charged sodium ion.
Attribution: Ting Wang - UC Davis (original work modified by Marc T. Facciotti)
Note: Possible discussion
Consider the model of water dissolving a salt crystal presented above. Describe in your own words how this model can be used to explain what is happening at the molecular level when enough salt is added to a volume of water that the salt no longer dissolves (the solution reaches saturation). Work together to craft a common picture.
Chemical equilibrium - Part 1: Forward and Reverse Reactions
The concept of chemical equilibrium is critical to following several of the discussions that we have in Bis2a and indeed throughout biology and the sciences. It is difficult to completely describe the concept of chemical equilibrium without reference to the energy of a system but for the sake of simplicity let’s try to anyway and reserve the discussion of energy for another chapter. Let us, rather, begin developing our understanding of equilibrium by considering the reversible reaction below:

Hypothetical reaction #1: A hypothetical reaction involving compounds A, B and D. If we read this from left-to-right we would say that A and B come together to form a larger compound D. Reading the reaction from right-to-left we would say that compound D breaks down into smaller compounds A and B.
We first need to define what is meant by a “reversible reaction”. This term “reversible” simply means that a reaction can proceed in both directions. That is, the things on the left side of the equation can react together to become the things on the right of the reaction AND the things on the right of the equation can also react together to become the things on the left side of the equation. Reactions in which the likelihood of the reaction happening in one of the two directions is vanishingly small - and thus only proceed in one direction small - are called irreversible reactions.
To start our discussion of equilibrium we begin by considering a reaction that we posit is readily reversible. In this case, it is the reaction depicted above: the imaginary formation of compound D from compounds A and B. Since it is a reversible reaction we could also call it the decomposition of D into A and B. Let us, however, imagine an experiment in which we watch the reaction proceed from a starting point where only A and B are present.
Example #1: Left-balanced reaction
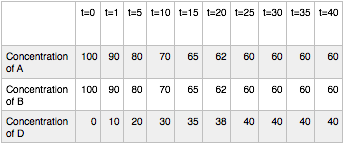
Hypothetical Reaction #1: time course
At time t = 0 (before the reaction starts) the reaction has 100 concentration units of compounds A and B and zero units of compound D. We now allow the reaction to proceed and observe the concentration of the three compounds over time (t=1, 5, 10, 15, 20, 25, 30, 35, and 40 time units). Notice that as A and B react D forms. In fact, one can see D forming from t=0 all the way to t=25. After that time, however, the concentrations of A, B and D stop changing. Once the reaction reaches the point where the concentrations of the components stop changing we say that the reaction has reached equilibrium. Notice that the concentrations of A, B and D are not equal at equilibrium. In fact, the reaction seems left balanced so that there is more A and B than D.
Note
****Common student misconception warning****
Many students fall victim to the misconception that the concentrations of a reaction’s reactants and products must be equal at equilibrium. Given that the term equilibrium sounds a lot like the word “equal” this is not surprising. But as the experiment above tries to illustrate, this is NOT correct!
Example #2: Right-balanced reaction
We can examine a second hypothetical reaction, the synthesis of compound J from the compounds E and F.

Hypothetical reaction #2: A hypothetical reaction involving compounds E, F and J. If we read this from left-to-right we would say that E and F come together to form a larger compound J. Reading the reaction from right-to-left we would say that compound J breaks down into smaller compounds E and F.
The structure of the hypothetical reaction #2 looks identical to the that of hypothetical reaction #1 that we considered above - two things come together to make one bigger thing. We just need to assume, in this case, that E, F and J have different properties from A, B and D. Let’s imagine a similar experiment to the one described above and examine this data:
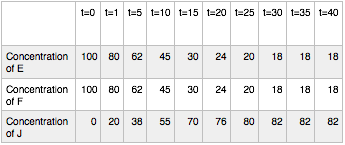
Hypothetical Reaction #2: time course
In this case, the reaction also reaches equilibrium. This time, however, equilibrium occurs at around t=30. After that point the concentrations of E, F and J do not change. Note again, that the concentrations of E, F and J are not equal at equilibrium. By contrast to hypothetical reaction #1 (the ABD reaction), this time the concentration of J, the thing on the right side of the arrows, is at a higher concentration than E and F. We say that this for this reaction, equilibrium lies to the right.
Four more points need to be made at this juncture.
- Point 1: Whether equilibrium for a reaction lies to the left or the right will be a function of the properties of the components of the reaction and the environmental conditions that the reaction is taking place in (e.g. temperature, pressure, etc.).
- Point 2: We can also talk about equilibrium using concepts of energy and we will do this soon - just not yet.
- Point 3: While hypothetical reactions #1 and #2 appear to reach a point where the reaction has “stopped” you should imagine that reactions are still happening even after equilibrium has been reached. At equilibrium the “forward” and “reverse” reactions are just happening at the same rate. That is, in example #2, at equilibrium J is forming from E and F at the same rate that it is breaking down into E and F. This explains how the concentrations of the compounds aren’t changing despite the fact that the reactions are still happening.
- Point 4: From this description of equilibrium we can define something we call the equilibrium constant. Typically the constant is represented by an uppercase K and may be written Keq. In terms of concentrations Keq is written as the mathematical product of the reaction product concentrations (stuff on the right) divided by the mathematical product of the reactant concentrations (stuff on the left). For example, Keq1 = [D]/[A][B] and Keq2 = [J]/[E][F]. The square brackets "[]" indicate “concentration of” whatever is inside the bracket.