21.2: Appendix B - Scientific Notation and Dilutions

Last updated
Save as PDF

Page ID: 122928

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

I. SCIENTIFIC NOTATION

When doing scientific calculations or writing, scientific notation is commonly used. In scientific notation, one digit (a number between 1 and 9) only is found to the left of the decimal point. The following examples are written in scientific notation:

3.17 x 10 ³
5.2 x 10 ^-2

Note that exponents (the powers of 10) are used in these conversions.

Multiples of 10 are expressed in positive exponents:

10 ⁰ = 1
10 ¹ = 10
10 ² = 100 = 10 x 10
10 ³ = 1000 = 10 x 10 x 10
10 ⁴ = 10,000 = 10 x 10 x 10 x 10
10 ⁵ = 100,000 = 10 x 10 x 10 x 10 x 10
10 ⁶ = 1,000,000 = 10 x 10 x 10 x 10 x 10 x 10

Fractions of 10 are expressed as negative exponents:

10 ^-1 = 0.1
10 ^-2 = 0.01 = 0.1 x 0.1
10 ^-3 = 0.001 = 0.1 x 0.1 x 0.1
10 ^-4 = 0.0001 = 0.1 x 0.1 x 0.1 x 0.1
10 ^-5 = 0.00001 = 0.1 x 0.1 x 0.1 x 0.1 x 0.1
10 ^-6 = 0.000001 = 0.1 x 0.1 x 0.1 x 0.1 x 0.1 x 0.1

A. Procedure for converting numbers that are multiples of 10 to scientific notation

1. Convert 365 to scientific notation.

a. Move the decimal point so that there is only one digit between 1 and 9 to the left of the point (from 365.0 to 3.65).

b. 3.65 is a smaller number than the original. To equal the original you would have to multiply 3.65 by 100. As shown above, 100 is represented by 10 ² . Therefore, the proper scientific notation of 365 would be 3.65 x 10 ² .

c. A simple way to look at these conversions is that you add a positive power of 10 for each place the original decimal is moved to the left. Since the decimal was moved two places to the left to get 3.65, the exponent would be 10 ² , thus 3.65 x 10 ² .

2. Convert 6,500,000 to scientific notation.

a. Move the decimal point so there is only one digit to the left of the point (6,500,000 becomes 6.5).

b. To equal the original number, you would have to multiply 6.5 by 1,000,000 or 10 ⁶ . (Since you moved the decimal point 6 places to the left, the exponent would be 10 ⁶ .)

c. Therefore, the proper scientific notation of 6,500,000 would be 6.5 x 10 ⁶ .

B. Procedure for converting numbers that are fractions of 10 to scientific notation.

1. Convert 0.0175 to scientific notation.

a. Move the decimal so there is one digit between 1 and 9 to the left of the decimal point (0.0175 becomes 1.75).

b. To equal the original number, you would have to multiply 1.75 by 0.01 or 10 ^-2 . Therefore, the proper scientific notation for 0.0175 would be 1.75 x 10 ^-2 .

c. A simpler way to look at these conversions is that you add a negative power of 10 for each place you move the decimal to the right. Since the decimal point was moved 2 places to the right, the exponent becomes 10 ^-2 , thus 1.75 x 10 ^-2 .

2. Convert 0.000345 to scientific notation.

a. Move the decimal point so only one digit (between 1 and 9) appears to the left of the decimal (0.000345 becomes 3.45).

b. To equal the original number, you would have to multiply 3.45 by 0.0001 or 10 ^-4 . (Since you moved the decimal point 4 places to the right, the exponent becomes 10 ^-4 .)

c. Therefore, the proper scientific notation of 0.000345 is 3.45 x 10 ^-4 .

C. Other examples

12,420,000 = 1.242 x 10 ⁷
21,300 = 2.13 x 10 ⁴
0.0047 = 4.7 x 10 ^-3
0.000006 = 6.0 x 10 ^-6

II. Dilutions: Examples

A. 1 ml of bacteria is mixed with 1 ml of sterile saline. The total ml in the tube would be 2 ml, of which 1 ml is bacteria. This is a 1:2 dilution (also written 1/2, meaning 1/2 as many bacteria per ml as the original ml).

B. 1 ml of bacteria is mixed with 3 ml of sterile saline. The total ml in the tube would be 4 ml, of which 1 ml is bacteria. This is then a 1:4 dilution (also written 1/4, meaning 1/4 as many bacteria per ml as the original ml).

C. 1 ml of bacteria is mixed with 9 ml of sterile saline. The total ml in the tube would be 10 ml, of which 1 ml is bacteria. This is then a 1:10 dilution (also written 1/10 or 10 ^-1 , meaning 1/10 or 10 ^-1 as many bacteria per ml as the original ml).

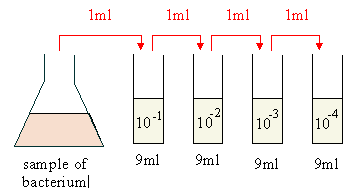
D. For dilutions greater than 1:10, usually serial dilutions (dilutions of dilutions) are made. The following represents a serial ten-fold dilution ( a series of 1:10 dilutions):

The dilution in tube #1 would be 1/10 or 10 ^-1 .
The dilution in tube #2 would be 1/100 or 10 ^-2 (1/10 of 1/10).
The dilution in tube #3 would be 1/1000 or 10 ^-3 (1/10 of 1/100).
The dilution in tube #4 would be 1/10,000 or 10 ^-4 (1/10 of 1/1000).

The dilution factor is the inverse of the dilution. (Inverse means you flip the two numbers of the fraction; with scientific notation you use the positive exponent.)

For a dilution of 1/2, the dilution factor would be 2/1 or 2.
For a dilution of 1/4, the dilution factor would be 4/1 or 4.
For a dilution of 1/10 or 10 ^-1 , the dilution factor would be 10/1 or 10 or 10 ¹ .
For a dilution of 1/1,000,000 or 10 ^-6 , the dilution factor would be 1,000,000/1 or 1,000,000 or 10 ⁶ .

n other words, the dilution factor tells you what whole number you have to multiply the dilution by to get back to the original 1 ml.