So far we have studied molecular aggregates (micelles and bilayers) and macromolecular structure (mostly proteins). Next we studied binding interactions which are the first steps in the expression of biological activity of a macromolecule. For some proteins, reversible binding is their sole function (consider the binding of dioxygen to myoglobin and hemoglobin). For many others, it is not. For those, what can happen next?
The answer to that question clearly depends on the biological function of the macromolecule. We can simplify this process by adding one additional step as reflected in the equilibrium binding expression shown below:
This expression indicates that the free ligand has changed in some fashion to x. In the next two chapters, we will consider two kinds of transformations:
This chapter will discuss diffusion processes. First, diffusion equations will be derived for cases not involving a binding receptor. The equation will show the rate of diffusion of a solute across a membrane from a region of high concentration to a region of low concentration (Δμ < 0) is a linear function of [ΔL] across the membrane. Next we will derive equations for receptor-mediated diffusion across a membrane - facilitated diffusion. We will deal with the situation when the solute must be transported up a concentration gradient (which requires ATP as an exogenous source of energy), a process called active transport, later in this web book.
PASSIVE DIFFUSION THROUGH A MEMBRANE - CASE 1: no receptor
 Java Applet: Before you study the derivation for simple passive diffusion, view the applet file below. First select clear to remove all molecules. Add 100 molecules to left. Move speed slider to left just until in indicates slow. Run the simulation. Count the number that move to the right hand side in 20 seconds. Refresh browser and repeat with 200 and then 300 on the left (unfortunately this slows down the molecules on the left so quantitation is impossible). Graph that number of molecules that moved to the right chamber (y axis) versus the the initial number on the left hand side (100, 200, and 300, respectively, x axis).
Java Applet: Before you study the derivation for simple passive diffusion, view the applet file below. First select clear to remove all molecules. Add 100 molecules to left. Move speed slider to left just until in indicates slow. Run the simulation. Count the number that move to the right hand side in 20 seconds. Refresh browser and repeat with 200 and then 300 on the left (unfortunately this slows down the molecules on the left so quantitation is impossible). Graph that number of molecules that moved to the right chamber (y axis) versus the the initial number on the left hand side (100, 200, and 300, respectively, x axis).
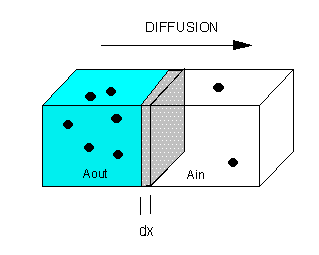
The flux of molecule A (JA) across a membrane of thickness dx, is proportional to the concentration gradient across the membrane, dA/dx., which is expressed as Fick's First Law of Diffusion:
\[ J_A \propto \dfrac{dA}{dx} \]
or
\[ J_A= - D \dfrac{dA}{dx} \]
where D is the diffusion coefficient. The negative sign is necessary since concentration increases in the opposite direction of net flux. For these derivations, we will assume the JA is the initial flux. That is, the flux is measured for a short enough time that the relative concentrations of A on both sides of the membrane does not change significantly. It should be clear that eventually the net flux levels off to zero, when the concentrations of A on both sides of the membrane are equal (i.e. the chemical potential of A on both sides is identical).
This can also be expressed as JA = -L dμA/dx , which bridges kinetic and thermodynamic aspects of diffusion.
For JA = - D dA/dx, dimensional analysis shows that
J = moles/area/sec = mol/cm2.s = - (cm2/s) mol/cm3/cm. Hence the units of D are cm2/s.
Rearranging Fick's Law gives the following:
\[J_A= - D \dfrac{dA}{dx} \]
\[ J_A dx = - D dA \]
Integrate both sides with x varying between 0 and x (the thickness of the membrane), and A from Aout to Ain.
JA x = -D [Ain - Aout] = D [Aout - Ain] or
JA = (D/x) [Aout - Ain] or
JA = P [Aout - Ain]
where P is the permeability coefficient, which has units of cm2/s/cm or cm/s. (We discussed permeability coefficients for different solutes traversing model bilayers when we discussed lipids.)
A plot of JA vs (Aout - Ain) is linear, with a slope of D/x



