Consider the following mechanism:
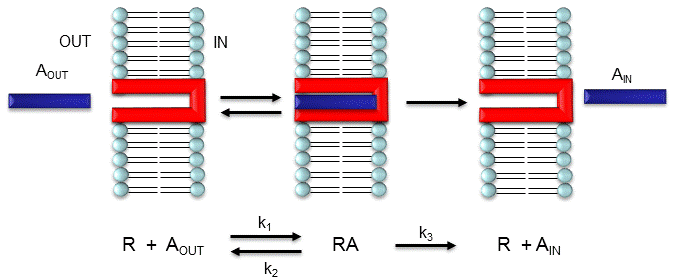
Let's assume that for this system the initial flux will be measured. We would like to derive equations which show \(J\) as a function of \(A_{out}\) (assuming that \(A_{in}\) is negligible over the time course of measuring the initial flux. Also assume that the \(J\) facilitated is much greater than \(J\) passive. In contrast to passive diffusion, JA is not proportional to \(A_{out}\) but rather to \([A_{bound}]\).
Consider this example to help you understand that proportionality. Pretend that the receptor is a truck which can carry one particle across the membrane at a time (i.e. 1/1 stoichiometry). Also assume that the particle can't get across without being carried by the truck. If there are no trucks in the membrane, no load can be delivered. If there are trucks in the membrane but no particles in them, no load will be delivered. As the number of particles available to be loaded into the truck increase, the truck will have an increased chance to be loaded (depending of course on the affinity of the particle for the truck). If the number of loaded trucks is doubled, the number of particles dumped to the other side will double. Therefore, by analogy, \(JA\) is proportional to \([RA]\):
\[\begin{align} JA &\propto [RA] \nonumber \\[5pt] &= k_3 [RA] \nonumber \end{align} \label{1}\]
How can we calculate \(RA\) when we know \(A\) and \(R\)? Let us assume that \(A_{total}\) (\(A_0\)) is much greater than \(R_0\), as is the likely biological case, and \(A_{in} = 0\). We can calculate \(RA\) using the following equations, and the same procedure we used for the derivation of the binding equation:
\[ ML = \dfrac{ M_oL}{K_d + L}\]
Dissociation constant:
\[ K_d = \dfrac{ [A]_{eq}[R]_{eq} }{[AR]_{eq}} = \dfrac{[A][R]}{[RA]} \label{2}\]
\(K_d\) has units of molarity.
Mass Balance of R:
\[R_o = R + RA \label{3A}\]
so
\[R = R_o -RA \label{3}\]
Since we will assume that \(A_o\) is much greater than \(R_0\), we will not need the mass balance for \(A\) (which is \(A_o = A + RA\))
Substitute Equation \ref{3} into \ref{2}:
\[ (RA)K_d = (Ro)A - (RRA)A \]
\[ (RA)K_d + (RA)A = (Ro)A \]
\[RA = (Ro)\dfrac{A}{K_d + A} \label{4}\]
Substitute \ref{4} into Equation \ref{1} gives the final equation,
\[JA = const [RA] = k_3 [RA] = k_3 (R_o) \dfrac{A}{K_d + A}. \label{5}\]
It should be clear to you from this equations that:
- a plot of \(JA\) vs. \(A\) is hyperbolic
- \(JA = 0\) when \(A = 0\).
- \(JA = J_{max}\) when \(A\) is much greater than \(K_d\)
- \(A = K_d\) when \(JA = J_{max}/2\).
 Wolfram Mathematica CDF Player - Jo vs A (free plugin required)
Wolfram Mathematica CDF Player - Jo vs A (free plugin required)
These are the same conditions we detailed for our understanding of the binding equation
\[ ML = \dfrac{ M_oL}{K_d + L}\]
RAPID EQUILIBRIUM ASSUMPTION
This derivation is based on the assumption that the relative concentrations of \(A\), \(R\), and \(AR\) can be determined by the \(K_d\) for the interactions and the concentrations of each species during the early part of diffusion (i.e. under initial rate conditions). Remember under these conditions, \(A_{out}\) does not change much with time. Is this a valid assumption? Examine the mechanism shown in the above figure. \(A_{out}\) binds to \(R\) with a second order rate constant \(k_1\). RA has two fates. It can dissociate with a first order rate constant \(k_2\) to Aout + R (to give the original species), or dissociate with a first order rate constant of k3 to give \(A_{in}\) + \(R\) (as A moves across the membrane). If we assume that \(k_2 \gg k_3\) (i.e. that the complex falls apart much more quickly than A is carried in), then the relative ratios of \(A\), \(R\), and \(RA\) can be described by \(K_d\). Alternatively, you can think about it this way. If \(A\) binds to \(R\), most of \(A\) will dissociate, and a small amount will be carried across the membrane. If this happened, then \(R\) is now free, and will quickly bind \(A_{out}\) and reequilibrate. This occurs since the most likely fate of bound A is to dissociate, not to be carried across the membrane, since \(k_3 \ll k_2\).
Diffusion of Ions and Molecules Across Membranes
As we saw previously, the permeability coefficients of synthetic membranes (liposomes) to solutes is related to the size and polarity of the solute.
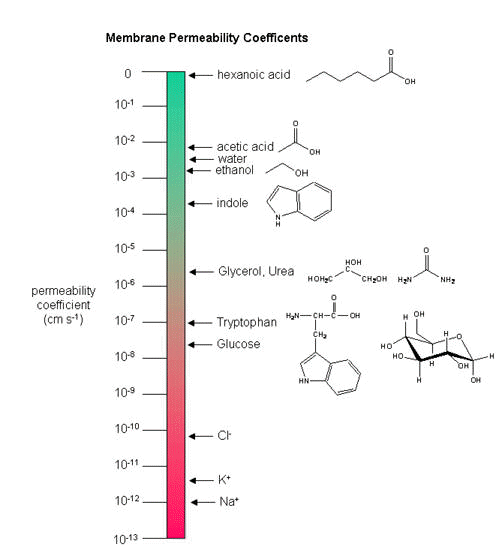
Figure: permeability coefficients
Smaller, higher charge density ions (like \(\ce{Na^{+}}\)) have a lower permeability coefficient than do larger, lower charge density ions (like \(\ce{K^{+}}\)). What about natural membranes? Look at the chart below.
Table 1: Permeability coefficient (cm/s) of natural and synthetic membranes to D-Glucose and D-mannitol at 25oC.
| Membrane Preparation |
D-Glucose |
D-Mannitol |
| Synthetic Lipid Bilayer |
\(2.4 \times 10^{-10}\) |
\(4.4 \times 10^{-11}\) |
| Calculated Passive Diffusion |
\(4 \times 10^{-9}\) |
\(3 \times 10^{-9}\) |
| Intact Human Erythrocyte (red blood cell) |
\(2.0 \times 10-4\) |
\(5 \times 10^{-9}\) |
Why do the permeability coefficients differ for D-Glc and D-Mannitol across the red blood cell membrane?
 Animation of Facilitated Diffusion
Animation of Facilitated Diffusion Animation of Diffusion and Active Transport from the HHMI
Animation of Diffusion and Active Transport from the HHMI
Contributors and Attributions




 Wolfram Mathematica CDF Player - Jo vs A (
Wolfram Mathematica CDF Player - Jo vs A (