5.6: Passive Transport - Diffusion
- Page ID
- 13086
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe diffusion and the factors that affect how materials move across the cell membrane.
Diffusion
Diffusion is a passive process of transport. A single substance tends to move from an area of high concentration to an area of low concentration until the concentration is equal across a space. You are familiar with diffusion of substances through the air. For example, think about someone opening a bottle of ammonia in a room filled with people. The ammonia gas is at its highest concentration in the bottle; its lowest concentration is at the edges of the room. The ammonia vapor will diffuse, or spread away, from the bottle; gradually, more and more people will smell the ammonia as it spreads. Materials move within the cell ‘s cytosol by diffusion, and certain materials move through the plasma membrane by diffusion. Diffusion expends no energy. On the contrary, concentration gradients are a form of potential energy, dissipated as the gradient is eliminated.
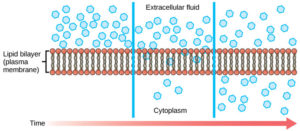
Each separate substance in a medium, such as the extracellular fluid, has its own concentration gradient independent of the concentration gradients of other materials. In addition, each substance will diffuse according to that gradient. Within a system, there will be different rates of diffusion of the different substances in the medium.
Factors That Affect Diffusion
Molecules move constantly in a random manner at a rate that depends on their mass, their environment, and the amount of thermal energy they possess, which in turn is a function of temperature. This movement accounts for the diffusion of molecules through whatever medium in which they are localized. A substance will tend to move into any space available to it until it is evenly distributed throughout it. After a substance has diffused completely through a space removing its concentration gradient, molecules will still move around in the space, but there will be no net movement of the number of molecules from one area to another. This lack of a concentration gradient in which there is no net movement of a substance is known as dynamic equilibrium. While diffusion will go forward in the presence of a concentration gradient of a substance, several factors affect the rate of diffusion:
- Extent of the concentration gradient: The greater the difference in concentration, the more rapid the diffusion. The closer the distribution of the material gets to equilibrium, the slower the rate of diffusion becomes.
- Mass of the molecules diffusing: Heavier molecules move more slowly; therefore, they diffuse more slowly. The reverse is true for lighter molecules.
- Temperature: Higher temperatures increase the energy and therefore the movement of the molecules, increasing the rate of diffusion. Lower temperatures decrease the energy of the molecules, thus decreasing the rate of diffusion.
- Solvent density: As the density of a solvent increases, the rate of diffusion decreases. The molecules slow down because they have a more difficult time getting through the denser medium. If the medium is less dense, diffusion increases. Because cells primarily use diffusion to move materials within the cytoplasm, any increase in the cytoplasm’s density will inhibit the movement of the materials. An example of this is a person experiencing dehydration. As the body’s cells lose water, the rate of diffusion decreases in the cytoplasm, and the cells’ functions deteriorate. Neurons tend to be very sensitive to this effect. Dehydration frequently leads to unconsciousness and possibly coma because of the decrease in diffusion rate within the cells.
- Solubility: As discussed earlier, nonpolar or lipid-soluble materials pass through plasma membranes more easily than polar materials, allowing a faster rate of diffusion.
- Surface area and thickness of the plasma membrane: Increased surface area increases the rate of diffusion, whereas a thicker membrane reduces it.
- Distance travelled: The greater the distance that a substance must travel, the slower the rate of diffusion. This places an upper limitation on cell size. A large, spherical cell will die because nutrients or waste cannot reach or leave the center of the cell. Therefore, cells must either be small in size, as in the case of many prokaryotes, or be flattened, as with many single-celled eukaryotes.
A variation of diffusion is the process of filtration. In filtration, material moves according to its concentration gradient through a membrane; sometimes the rate of diffusion is enhanced by pressure, causing the substances to filter more rapidly. This occurs in the kidney where blood pressure forces large amounts of water and accompanying dissolved substances, or solutes, out of the blood and into the renal tubules. The rate of diffusion in this instance is almost totally dependent on pressure. One of the effects of high blood pressure is the appearance of protein in the urine, which is “squeezed through” by the abnormally high pressure.
Key Points
- Substances diffuse according to their concentration gradient; within a system, different substances in the medium will each diffuse at different rates according to their individual gradients.
- After a substance has diffused completely through a space, removing its concentration gradient, molecules will still move around in the space, but there will be no net movement of the number of molecules from one area to another, a state known as dynamic equilibrium.
- Several factors affect the rate of diffusion of a solute including the mass of the solute, the temperature of the environment, the solvent density, and the distance traveled.
Key Terms
- diffusion: The passive movement of a solute across a permeable membrane
- concentration gradient: A concentration gradient is present when a membrane separates two different concentrations of molecules.


