6.1: Dihybrid Crosses
- Page ID
- 4087
Mendel’s Second Law
Before Mendel, it had not yet been established that heritable traits were controlled by discrete factors. Therefor an important question was therefore whether distinct traits were controlled by discrete factors that were inherited independently of each other? To answer this, Mendel took two apparently unrelated traits, such as seed shape and seed color, and studied their inheritance together in one individual. He studied two variants of each trait: seed color was either green or yellow, and seed shape was either round or wrinkled. (He studied seven traits in all.) When either of these traits was studied individually, the phenotypes segregated in the classical 3:1 ratio among the progeny of a monohybrid cross (Figure \(\PageIndex{2}\)), with ¾ of the seeds green and ¼ yellow in one cross, and ¾ round and ¼ wrinkled in the other cross. Would this be true when both were in the same individual?

To analyze the segregation of both traits at the same time in the same individual, he crossed a pure breeding line of green, wrinkled peas with a pure breeding line of yellow, round peas to produce F1 progeny that were all green and round, and which were also dihybrids; they carried two alleles at each of two loci (Figure \(\PageIndex{3}\)).
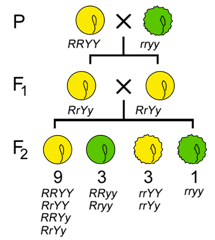
If the inheritance of seed color was truly independent of seed shape, then when the F1 dihybrids were crossed to each other, a 3:1 ratio of one trait should be observed within each phenotypic class of the other trait (Figure \(\PageIndex{3}\)). Using the product law, we would therefore predict that if ¾ of the progeny were green, and ¾ of the progeny were round, then ¾ × ¾ = 9/16 of the progeny would be both round and green (Table \(\PageIndex{1}\)). Likewise, ¾ × ¼ = 3/16 of the progeny would be both round and yellow, and so on. By applying the product rule to all of these combinations of phenotypes, we can predict a 9:3:3:1 phenotypic ratio among the progeny of a dihybrid cross, if certain conditions are met, including the independent segregation of the alleles at each locus. Indeed, 9:3:3:1 is very close to the ratio Mendel observed in his studies of dihybrid crosses, leading him to state his Second Law, the Law of Independent Assortment, which we now express as follows: two loci assort independently of each other during gamete formation.
Two loci assort independently of each other during gamete formation.
|
Frequency of phenotypic crosses within separate monohybrid crosses: seed shape: ¾ round ¼ wrinkled seed color: ¾ yellow ¼ green Frequency of phenotypic crosses within a dihybrid cross: ¾ round × ¾ yellow = 9/16 round & yellow ¾ round × ¼ green = 3/16 round & green ¼ wrinkled × ¾ yellow = 3/16 wrinkled & yellow ¼ wrinkled × ¼ green = 1/16 wrinkled & green |
The 9:3:3:1 phenotypic ratio that we calculated using the product rule can also be obtained using Punnett Square (Figure \(\PageIndex{4}\)). First, we list the genotypes of the possible gametes along each axis of the Punnett Square. In a diploid with two heterozygous genes of interest, there are up to four combinations of alleles in the gametes of each parent. The gametes from the respective rows and column are then combined in the each cell of the array. When working with two loci, genotypes are written with the symbols for both alleles of one locus, followed by both alleles of the next locus (e.g. AaBb, not ABab). Note that the order in which the loci are written does not imply anything about the actual position of the loci on the chromosomes.
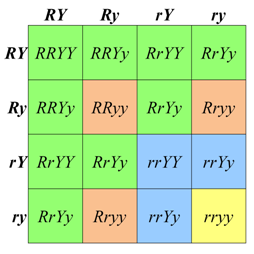
To calculate the expected phenotypic ratios, we assign a phenotype to each of the 16 genotypes in the Punnett Square, based on our knowledge of the alleles and their dominance relationships. In the case of Mendel’s seeds, any genotype with at least one R allele and one Y allele will be round and yellow; these genotypes are shown in the nine, green-shaded cells in Figure \(\PageIndex{4}\). We can represent all of four of the different genotypes shown in these cells with the notation (R_Y_), where the blank line (__), means “any allele”. The three offspring that have at least one R allele and are homozygous recessive for y (i.e. R_yy) will have a round, green phenotype. Conversely the three progeny that are homozygous recessive r, but have at least one Y allele (rrY_) will have wrinkled, yellow seeds. Finally, the rarest phenotypic class of wrinkled, yellow seeds is produced by the doubly homozygous recessive genotype, rryy, which is expected to occur in only one of the sixteen possible offspring represented in the square.
Assumptions of the 9:3:3:1 ratio
Both the product rule and the Punnett Square approaches showed that a 9:3:3:1 phenotypic ratio is expected among the progeny of a dihybrid cross such as Mendel’s RrYy × RrYy. In making these calculations, we assumed that:
- both loci assort independently;
- one allele at each locus is completely dominant; and
- each of four possible phenotypes can be distinguished unambiguously, with no interactions between the two genes that would alter the phenotypes.
Deviations from the 9:3:3:1 phenotypic ratio may indicate that one or more of the above conditions has not been met. Modified ratios in the progeny of a dihybrid cross can therefore reveal useful information about the genes involved.
Linkage is one of the most important reasons for distortion of the ratios expected from independent assortment. Linked genes are located close together on the same chromosome. This close proximity alters the frequency of allele combinations in the gametes. We will return to the concept of linkage in Chapter 7. Deviations from 9:3:3:1 ratios can also be due to interactions between genes. These interactions will be discussed in the remainder of this chapter. For simplicity, we will focus on examples that involve easily scored phenotypes, such as pigmentation. Nevertheless, keep in mind that the analysis of segregation ratios of any markers can provide insight into a wide range of biological processes they represent.


