Skip to main content
Biology LibreTexts

1.6: The law of independent assortment

  1. Last updated
  2. Save as PDF
  • Page ID
    73823

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Introduction

    The law of segregation lets us predict how a single feature associated with a single gene is inherited. In some cases, though, we might want to predict the inheritance of two characteristics associated with two different genes. How can we do this?

    [Refresher on the law of segregation]

    The law of segregation states that each gamete (sperm or egg cell) made by an organism will get just one of the two gene copies present in a parent organism, and that the gene copies are randomly allocated to the gametes. For instance, if an organism has a genotype of Aa, half of its gametes will contain an A allele, and the other half will contain an a allele.

    You can use the link at the start of the paragraph to learn more about the law of segregation.

    To make an accurate prediction, we need to know whether the two genes are inherited independently or not. That is, we need to know whether they "ignore" one another when they're sorted into gametes, or whether they "stick together" and get inherited as a unit.

    When Gregor Mendel asked this question, he found that different genes were inherited independently of one another, following what's called the law of independent assortment. In this article, we'll take a closer look at the law of independent assortment and how it is used to make predictions. We'll also see when and why the law of independent assortment does (or doesn't!) hold true.

    Note: If you are not yet familiar with how individual genes are inherited, you may want to check out the article on the law of segregation or the introduction to heredity video before you dive into this article.

    What is the law of independent assortment?

    Mendel's law of independent assortment states that the alleles of two (or more) different genes get sorted into gametes independently of one another. In other words, the allele a gamete receives for one gene does not influence the allele received for another gene.

    Example: Pea color and pea shape genes

    Let's look at a concrete example of the law of independent assortment. Imagine that we cross two pure-breeding pea plants: one with yellow, round seeds (YYRR) and one with green, wrinkled seeds (yyrr). Because each parent is homozygous, the law of segregation tells us that the gametes made by the wrinkled, green plant all are ry, and the gametes made by the round, yellow plant are all RY. That gives us F1 offspring that are all RrYy.

    The allele specifying yellow seed color is dominant to the allele specifying green seed color, and the allele specifying round shape is dominant to the allele specifying wrinkled shape, as shown by the capital and lower-case letters. This means that the F1 plants are all yellow and round. Because they are heterozygous for two genes, the F1 plants are called dihybrids (di- = two, -hybrid = heterozygous).

    A cross between two dihybrids (or, equivalently, self-fertilization of a dihybrid) is known as a dihybrid cross. When Mendel did this cross and looked at the offspring, he found that there were four different categories of pea seeds: yellow and round, yellow and wrinkled, green and round, and green and wrinkled. These phenotypic categories (categories defined by observable traits) appeared in a ratio of approximately 9:3:3:1.

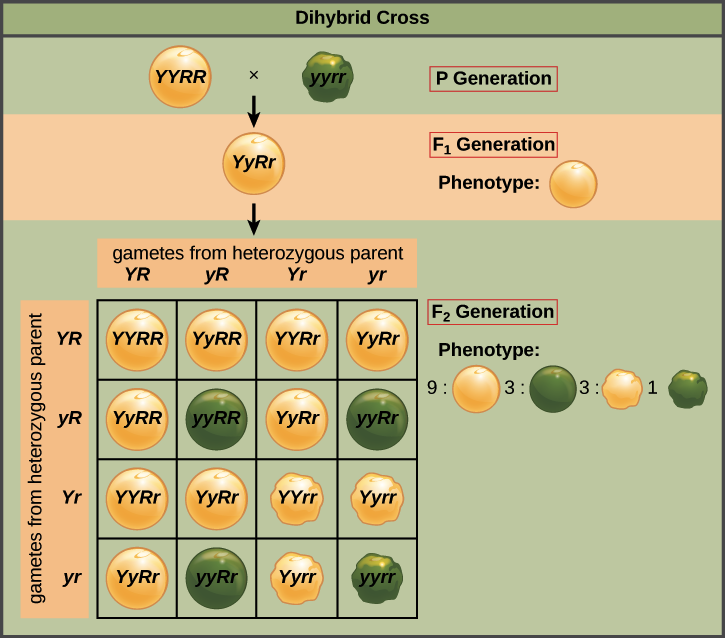
    Illustration of the hypothesis that the seed color and seed shape genes assort independently. In this diagram, the Y and R alleles of the yellow, round parent and the y and r alleles of the green, wrinkled parent are not inherited as units. Instead, the alleles of the two genes are inherited as independent units. P generation: A yellow, round plant (YYRR) is crossed with a green, wrinkled plant (yyrr). Each parental generation can produce only one type of gamete, YR or yr. F1 generation: The F1 dihybrid seeds are yellow and round, with a genotype of YyRr. The F1 plants can produce four different types of gametes: YR, Yr, yR, and yr. We can predict the genotypes of the F2 plants by placing these gametes along the top and side axes of a 4X4 Punnett square and filling in the boxes to represent fertilization events. F2 generation: Completion of the Punnett square predicts four different phenotypic classes of offspring, yellow/round, yellow/wrinkled, green/round, and green/wrinkled, in a ratio of 9:3:3:1. This is the prediction of the model in which the seed shape and seed color genes assort independently. Punnett square:||YR|Yr|yR|yr-|-|-|-|-|-YR||YYRR|YYRr|YyRR|YyRrYr||YYRr|_YYrr_|YyRr|_Yyrr_yR||YyRR|YyRr|**yyRR**|**yyRr**yr||YyRr|_Yyrr_|**yyRr**|***yyrr***Plain text = yellow, round phenotype_Italic text_ = yellow, wrinkled phenotype**Bold text** = green, round phenotype***Bold, italic text*** = green, wrinkled phenotype
    Image credit: "Laws of inheritance: Figure 2," by OpenStax College, Biology, CC BY 4.0.

    This ratio was the key clue that led Mendel to the law of independent assortment. That's because a 9:3:3:1 ratio is exactly what we'd expect to see if the F1 plant made four types of gametes (sperm and eggs) with equal frequency: YR, Yr, yR, and yr. In other words, this is the result we'd predict if each gamete randomly got a Y or y allele, and, in a separate process, also randomly got an R or r allele (making four equally probable combinations).

    We can confirm the link between the four types of gametes and the 9:3:3:1 ratio using the Punnett square above. To make the square, we first put the four equally probable gamete types along each axis. Then, we join gametes on the axes in the boxes of the chart, representing fertilization events. The 16 equal-probability fertilization events that can occur among the gametes are shown in the 16 boxes. The offspring genotypes in the boxes correspond to a 9:3:3:1 ratio of phenotypes, just as Mendel observed.

    [More about two-gene Punnett squares]

    We can draw a Punnett square for a two-gene scenario by following the same basic rules as for a monohybrid cross, placing the gametes along the axes and combining them in the squares to represent fertilization events. However, since there are now more gamete types, there must also be more squares in the table: 4 possible types of maternal gametes x 4 possible types of paternal gametes = 16 squares total.

    As with a single-gene Punnett square, we place all the possible types of gametes along the axes, then combine them in the squares where the columns and rows intersect to represent fertilization events (the formation of zygotes, or offspring).

    To learn how you can use the rules of probability to predict the outcome of a dihybrid cross, see the probabilities in genetics article.

    Independent assortment vs. linkage

    The section above gives us Mendel's law of independent assortment in a nutshell, and lets us see how the law of independent assortment leads to a 9:3:3:1 ratio. But what was the alternative possibility? That is, what would happen if two genes didn't follow independent assortment?

    In the extreme case, the genes for seed color and seed shape might have always been inherited as a pair. That is, the yellow and round alleles might always have stayed together, and so might the green and wrinkled alleles.

    To see how this could work, imagine that the color and shape genes are physically stuck together and cannot be separated, as represented by the boxes around the alleles in the diagram below. For instance, this could happen if the two genes were located very, very close together on a chromosome (an idea we'll explore further at the end of the article).

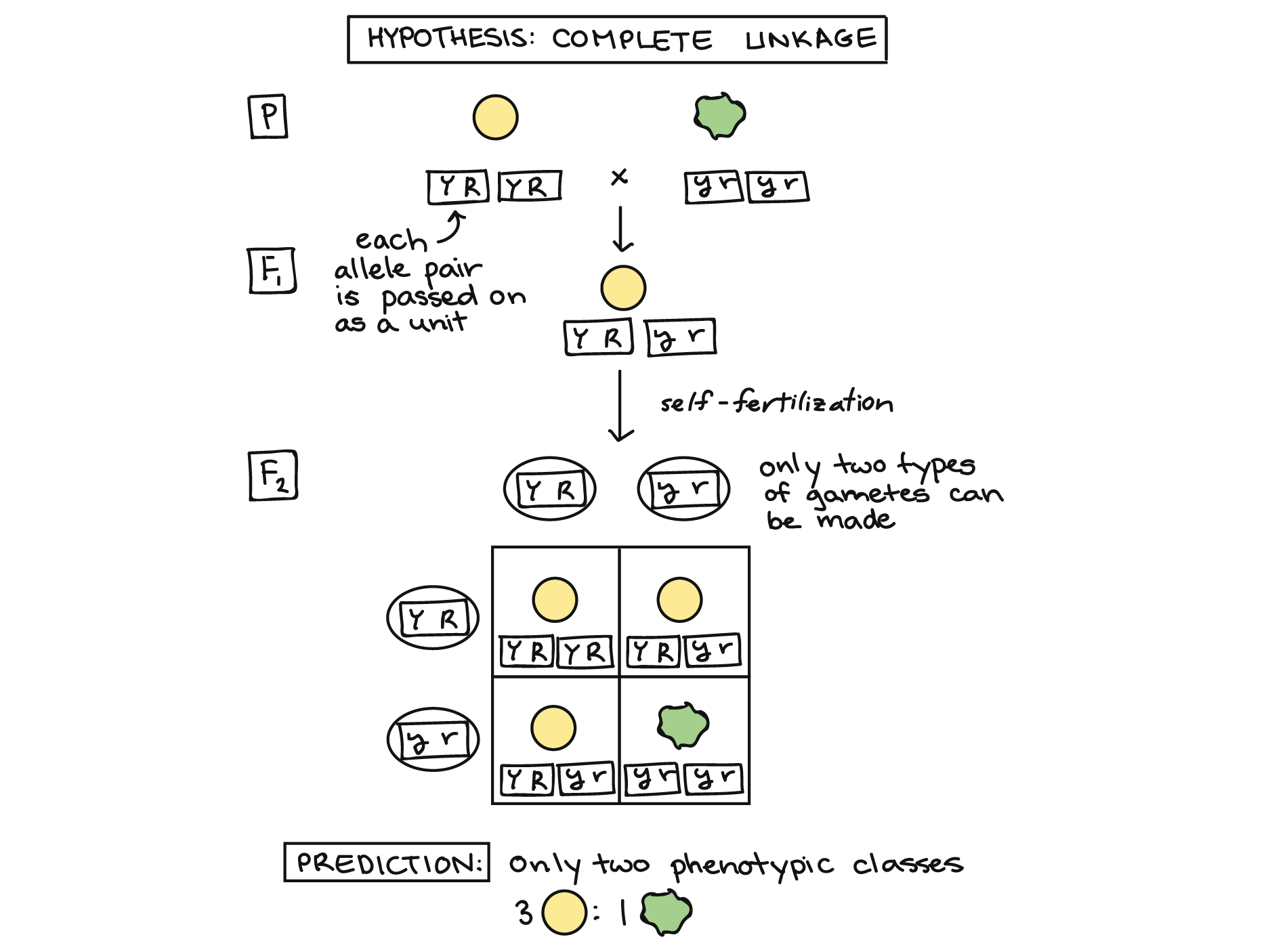
    Illustration of the hypothesis that the seed shape and seed color genes display complete linkage. In this diagram, the Y and R alleles are represented as a unit (Y-R), as are the y and r alleles (y-r). P generation: a (Y-R)(Y-R) yellow, round parent is crossed with a (y-r)(y-r) green, wrinkled parent. Each parent produces just one type of gamete, containing either a (Y-R) unit or a (y-r) unit. F1 generation: the F1 dihybrid is heterozygous for both genes and has a yellow, round phenotype. The allele pairs remain as indivisible units in the F1 dihybrid: (Y-R)(y-r). When the F1 dihybrid self-fertilizes, it can produce two types of gametes: a gamete containing a (Y-R) unit and a gamete containing a (y-r) unit. These two types of gametes will each be produced 50% of the time, and we can predict the genotypes of the F2 offspring by listing the two gamete types along the axes of a 2X2 Punnett square and then filling in the boxes to simulate fertilization events. F2 generation: When the Punnett square is completed, we get three different genotypes in a 1:2:1 ratio: (Y-R)(Y-R), (Y-R)(y-r), and (y-r)(y-r). These genotypes correspond to a 3:1 ratio of yellow, round:green, wrinkled seeds. This is the prediction of the model in which the seed shape and seed color genes are completely linked. (Note: this model is not actually correct for these two genes. This is just one of the two hypotheses that Mendel was testing).

    Rather than giving a color allele and, separately, giving a shape allele to each gamete, the F1 dihybrid plant would simply give one “combo unit” to each gamete: a YR allele pair or a yr allele pair.

    We can use a Punnett square to predict the results of self-fertilization in this case, as shown above. If the seed color and seed shape genes were in fact always inherited as a unit, or completely linked, a dihybrid cross should produce just two types of offspring, yellow/round and green/wrinkled, in a 3:1 ratio. Mendel's actual results were quite different from this (the 9:3:3:1 ratio we saw earlier), telling him that the genes assorted independently.

    The reason for independent assortment

    To see why independent assortment happens, we need to fast-forward half a century and discover that genes are physically located on chromosomes. To be exact, the two copies of a gene carried by an organism (such as a Y and a y allele) are located at the same spot on the two chromosomes of a homologous pair. Homologous chromosomes are similar but non-identical, and an organism gets one member of the pair from each of its two parents.

    The physical basis for the law of independent assortment lies in meiosis I of gamete formation, when homologous pairs line up in random orientations at the middle of the cell as they prepare to separate. We can get gametes with different combos of "mom" and "dad" homologues (and thus, the alleles on those homologues) because the orientation of each pair is random.

    To see what this means, compare chromosome arrangement 1 (top) and chromosome arrangement 2 (bottom) at the stage of metaphase I in the diagram below. In one case, the red "mom" chromosomes go together, while in the other, they split up and mix with the blue "dad" chromosomes. If meiosis happens many times, as it does in a pea plant, we will get both arrangements—and thus RY, Ry, rY, and ry classes of gametes—with equal frequency.

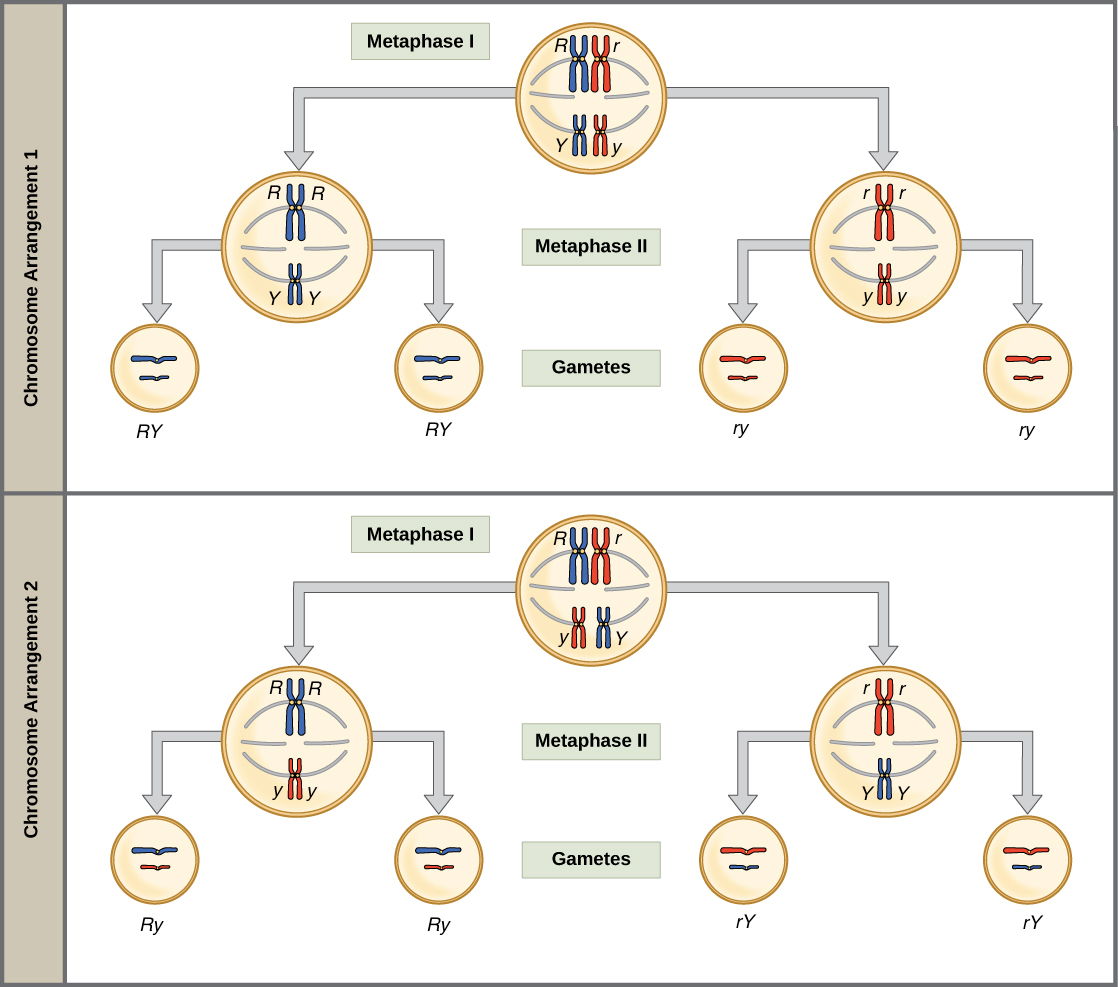
    Homologous pairs of chromosomes line up at the metaphase plate during metaphase I of meiosis. The homologous chromosomes, with their different versions of each gene, are randomly segregated into daughter nuclei, resulting in a variety of possible genetic arrangements.
    Image modified from "The laws of inheritance: Figure 5," by OpenStax College, Concepts of Biology, CC BY 4.0

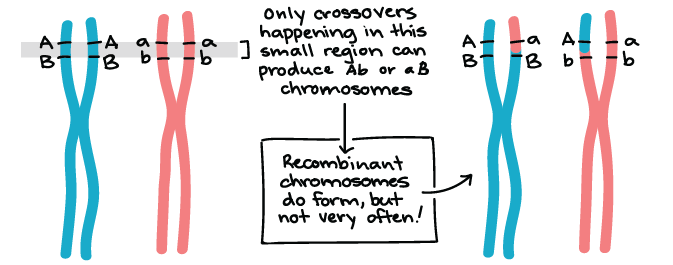
    Genes that are on different chromosomes (like the Y and R genes) assort independently. The seed color and seed shape genes are on chromosomes 1 and 7 of the pea genome, respectively, in real life1. Genes that are far apart on the same chromosome also assort independently thanks to the crossing over, or exchange of homologous chromosome bits, that occurs early in meiosis I.

    [See a picture]

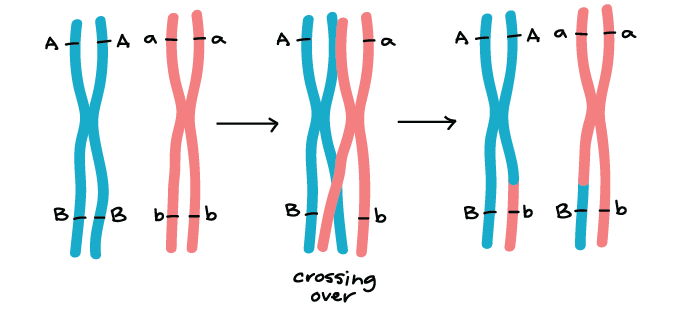
    Illustration of crossing over

    There are, however, gene pairs that do not assort independently. When genes are close together on a chromosome, the alleles on the same chromosome tend to be inherited as a unit more frequently than not. Such genes do not display independent assortment and are said to be linked. We'll take a closer look at genetic linkage in other articles and videos.

    [See a picture]

    Illustration of genes close together on a chromosome. Recombinant chromosomes do form, but not very often.

    Check your understanding

    Query \(\PageIndex{1}\)

    [Hint]

    Since all of the F1 dogs are black and straight-furred, we know that black fur color and straight fur texture are dominant over yellow fur color and curly fur texture. If we call the color gene B/b and the texture gene C/c, and use capital letters for the dominant form of each gene and lowercase letters for the recessive form, we can assign the two parental dogs genotypes of BBcc (black and curly) and bbCC (yellow and straight-furred). When the parental dogs are crossed, they produce black, straight-furred F1 dogs that are dihybrids: BbCc.

    A cross between two F1 dihybrid dogs results in the Punnett square shown below. The F1 dogs can make four different types of gametes, which are represented along the two axes of the Punnett square. The squares of the table represent fertilization events in which the gametes on the axes combine. Since all of the gamete types are equally likely to be produced (because the genes assort independently, i.e., do not influence each other's inheritance), all the squares in the table represent equal-probability events, ones that occur 1/16 of the time.

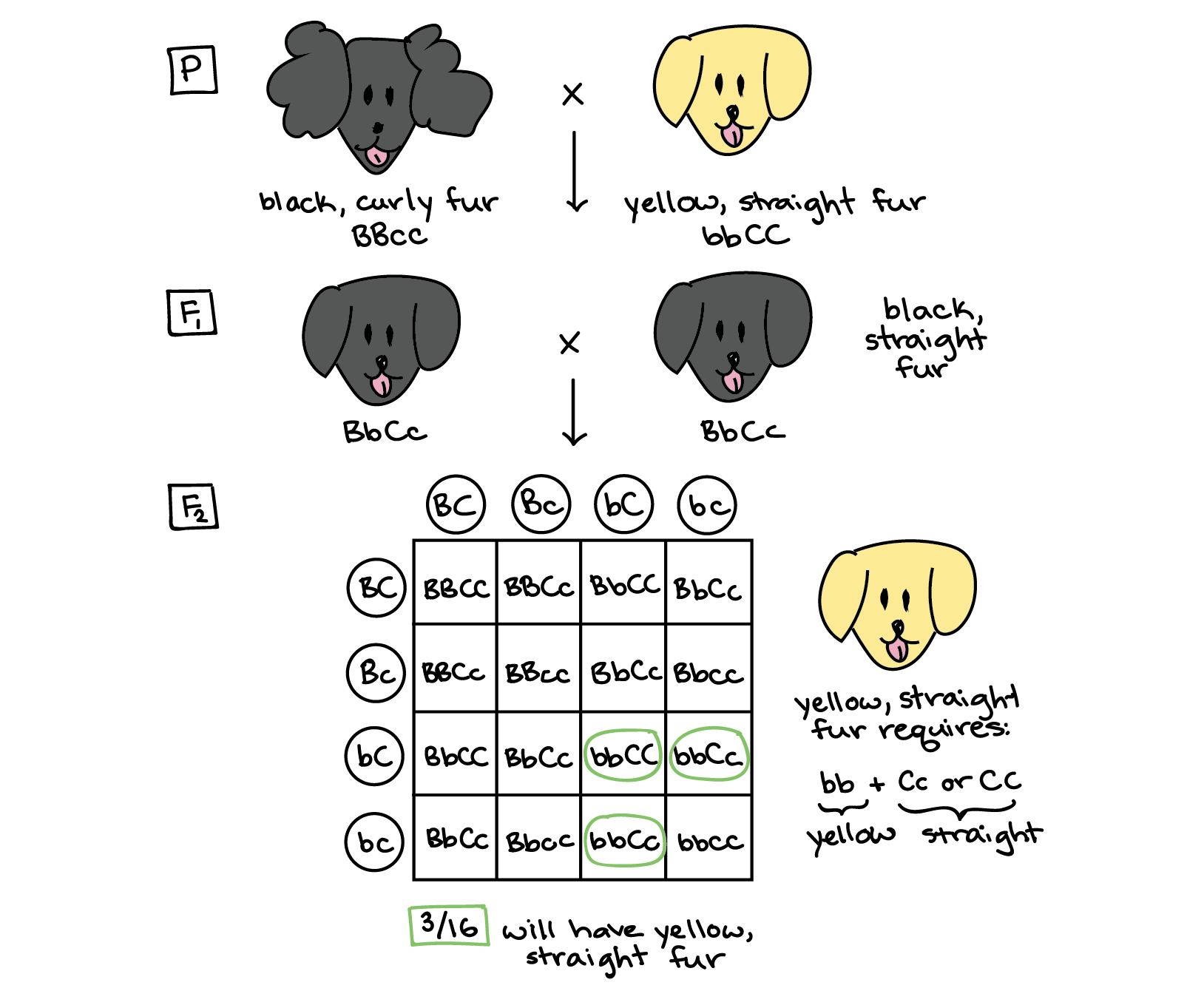
    Annotated diagram illustrating the solution to the dog fur problem. P generation: Black, curly-furred parent is of genotype BBcc. Yellow, straight-furred parent is of genotype bbCC. F1 generation: All F1 dogs are of genotype BbCc. The F1 dogs are interbred to produce an F2 generation. F2 generation: Punnett square:||BC|Bc|bC|bc-|-|-|-|-|-BC||BBCC|BBCc|BbCC|BbCcBc||BBCc|BBcc|BbCc|BbccbC||BbCC|BbCc|**bbCC**|**bbCc**bc||BbCc|Bbcc|**bbCc**|bbcc Puppies of bbCC or bbCc genotypes will be yellow and have straight fur. 3 out of the 16 boxes of the Punnett square correspond to these genotypes.

    Now, we need to find the squares that correspond to the outcome we are interested in: a puppy with yellow, straight fur. To have yellow, straight fur, the puppy must get two recessive alleles for fur color (bb genotype) and at least one dominant allele for fur texture (Cc or CC genotype). If we go through the table and circle the genotypes that match these requirements, we'll find that 3 out of the 16 boxes correspond to yellow, straight-furred puppies. Thus, we would expect 3/16 of the F2 puppies to have yellow, straight fur.

    Answer: 3/16.

    Contributors and Attributions

    • Khan Academy (CC BY-NC-SA 3.0; All Khan Academy content is available for free at www.khanacademy.org)

    [Attribution and references]

    Attribution:

    This article is a modified derivative of:

    The modified article is licensed under a CC BY-NC-SA 4.0 license.

    Works cited:

    1. Reid, J. B., and Ross, J. J. (2011). Mendel's genes: Towards a full molecular characterization. Genetics 189(1), 3-10. http://dx.doi.org/10.1534/genetics.111.132118. Retrieved from www.ncbi.nlm.nih.gov/pmc/articles/PMC3176118/.

    References:

    Dihybrid. (2015). In The free dictionary. Retrieved from http://www.thefreedictionary.com/dihybrid.

    Kimball, J. W. (2014, April 21). Genetic linkage and genetic maps. In Kimball's biology pages. Retrieved from https://www.biology-pages.info/L/Linkage.html

    Purves, W. K., Sadava, D. E., Orians, G. H., and Heller, H.C. (2004). Genetics: Mendel and beyond. In Life: The science of biology (7th ed., pp. 187-212). Sunderland, MA: Sinauer Associates.

    Raven, P. H., Johnson, G. B., Mason, K. A., Losos, J. B., and Singer, S. R. (2014). Patterns of inheritance. In Biology (10th ed., AP ed., pp. 221-238). New York, NY: McGraw-Hill.

    Reece, J. B., Urry, L. A., Cain, M. L., Wasserman, S. A., Minorsky, P. V., and Jackson, R. B. (2011). Mendel and the gene idea. In Campbell Biology (10th ed., pp. 267-291). San Francisco, CA: Pearson.

    Reid, J. B., and Ross, J. J. (2011). Mendel's genes: Towards a full molecular characterization. Genetics 189(1), 3-10. http://dx.doi.org/10.1534/genetics.111.132118. Retrieved from www.ncbi.nlm.nih.gov/pmc/articles/PMC3176118/.

    The Adapa Project. (2014, August 13). What are the laws of segregation and independent assortment and why are they so important? In BioBook. Retrieved from https://adapaproject.org/bbk_temp/tiki-index.php?page=Leaf%3A+What+are+the+laws+of+segregation+and+independent+assortment+and+why+are+they+so+important%3F.

    1.6: The law of independent assortment is shared under a CC BY-NC-SA 3.0 license and was authored, remixed, and/or curated by LibreTexts.