17.1: Chapter Introduction

In Equation 8.1, mutualism occurs when the interaction terms, \(s_{1,2}\) and \(s_{2,1}\), are both positive. This is the defining feature of mutualism. The self-engagement terms, \(s_{1,1}\) and \(s_{2,2}\), may be positive or negative, and the intrinsic growth terms, \(r_1\) and \(r_2\), may also be positive or negative.

If both growth terms \(r_i\) are positive, then either species can survive on its own, without the presence of the other. This is called “facultative mutualism.” An example is the mutualism between oxpecker and warthog (Figure 9.2 left). Oxpeckers have other sources for food, and warthogs may suffer but likely not die from larger parasite loads.

If the \(r_i\) are both negative, then neither species can survive on its own without the presence of the other. This is called “obligate mutualism.” An example is lichen, composed of an algae and a fungus. If the fungus alone is placed on a rock, it will die. Although it can eat rock—or, more accurately, can dissolve nutrients from rock—it cannot produce carbon compounds from rock. And if the algae alone is placed on a rock, it will die. Although it can produce carbon compounds from the air through photosynthesis, it cannot eat rock. But the two together become a perfect partnership, each covering the other’s weaknesses.

Figure \(\PageIndex{1}\). Photosynthesis is the basis of many mutualisms. Euglena is a protist–chloroplast combination that can fix carbon dioxide from the water, changing the nature of the protist, and can move distances following nutrients, supporting the chloroplast. Chloroplasts appear to be much-modified cyanobacteria, rendered wholly dependent on their partners by eons of evolution (left, through a microscope). Lichens are fungal–algal combinations in which the algal component can fix carbon and the fungal component can dissolve nutrients from rock (middle, shoulder height). Coral are anthozoa—marine animals with stinging tentacles to capture food—that are often reef-building and associated with marine algae. A significant fraction of the world’s carbon is sequestered in coral reefs (right, from space).

When \(r_1\) is positive and \(r_2\) is negative, or vice versa, it is a partially obligate mutualism. One species depends on a second, but the second can get along without the first. This is a mathematical possibility, and some cases such as chloroplast– euglena may be examples (Figure \(\PageIndex{1}\) left), where the chloroplast cannot live without the protist, but the protist can.

Besides obligate versus facultative mutualism, there is another major distinction. This is between “restrained” and “unrestrained” mutualism. This distinction is not typically made in textbooks because it is related to the difference between logistic and orthologistic population growth, which typically is not covered.

When self-limiting effects of terms \(s_{1,1}\) and \(s_{2,2}\) are stronger than the interspecies enhancement terms \(s_{1,2}\) and \(s_{2,1}\), the mutualistic pair has a carrying capacity that can be computed from the properties of the individual species. They reach their joint carrying capacity along a path that looks like logistic growth, and is identical in form to that of two competing species that coexist and reach a joint carrying capacity. However, when the self-limiting effects of \(s_{1,1}\) and \(s_{2,2}\) are weaker than the inter-species enhancement terms \(s_{1,2}\) and \(s_{2,1}\), the carrying capacity of the pair of species cannot be computed from the value of those parameters, and they increase ever more rapidly until some other limitation is hit.

Think about lichen again. The carrying capacity of each species is essentially zero when they are living separately on the surface of a rock. Together, however, they can cover the rock, and their joint carrying capacity on Earth is related to the total area of rocks on Earth—plus other suitable habitat such as the bark of trees, the exterior surface of an automobile junked and neglected for decades, and myriad other surfaces otherwise uninhabitable. The area of rocks in the world, and other suitable surfaces, certainly is not part of the r_i and s_i,j parameters! This is quite unlike the situation for competition and predation, in which the joint carrying capacity is encoded in the parameters. Why this should be is revealed by some diagrams and corresponding mathematics.

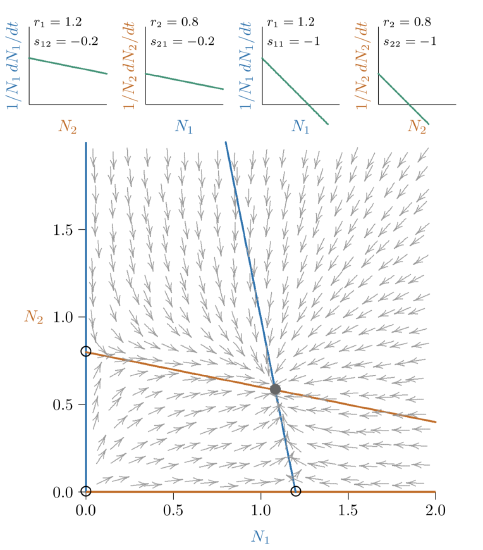
Figure \(\PageIndex{2}\). Phase space for competition weaker than that of Figure 10.11. The joint equilibrium (black-filled circle) is closer along the axes to the individual carrying capacities (open circles).

Figure \(\PageIndex{3}\). Phase space for mild mutualism, causing the opposite effect of that shown in Figure \(\PageIndex{2}\). The joint equilibrium is larger than the individual carrying capacities.

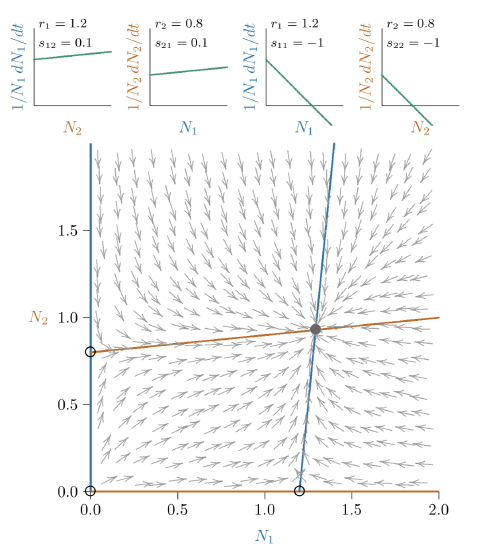
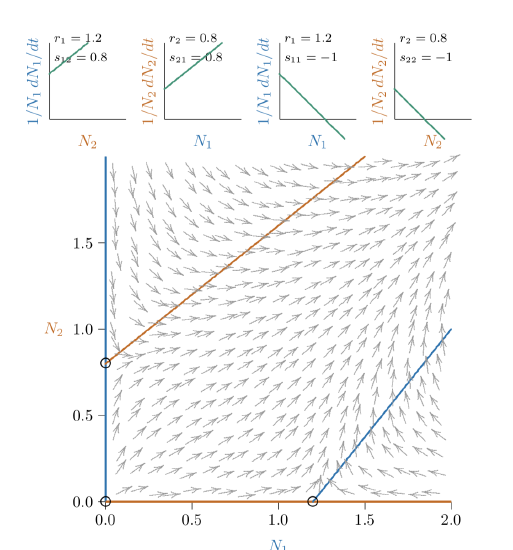
Figure \(\PageIndex{4}\) Phase space for stronger mutualism, but still restrained, because a joint equilibrium still exists (though far off the chart at the intersection of the red and blue isoclines).

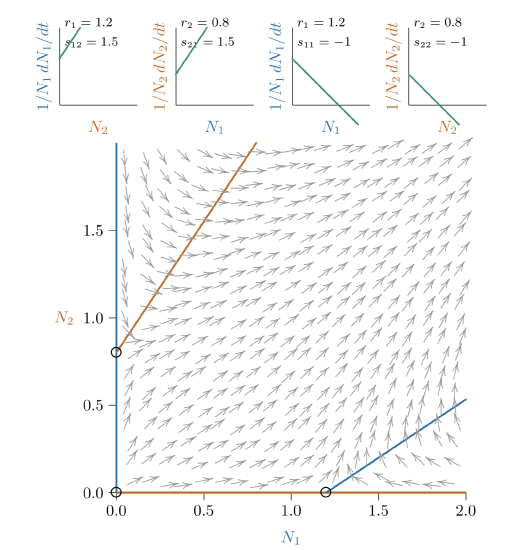
Figure \(\PageIndex{5}\). With slightly stronger mutualism still, the joint equilibrium vanishes—cannot be determined from the parameters— and the mutualistic relationship becomes “unrestrained.”

Figure \(\PageIndex{6}\). As mutualistic species become more dependent upon each other, their individual carrying capacities become smaller (open circles here are closer to the origin).

Figure \(\PageIndex{7}\). Finally, in obligate mutualisms, individual carrying capacities vanish and an Allee point arises (open circle). Extinction becomes a present danger (closed circle).