9.5: Hidden Markov Chains
- Page ID
- 40970
A toy Hidden Markov Model is a generative approach to model this behavior. Each emission of the HMM is one DNA base/letter. The hidden states of the model are intergenic, exon, intron. Improving upon this model would involve including hidden states DonorG and DonorT. The DonorG and DonorT states utilize the information that exons are delineated by GT at the end of the sequence before the start of an intron. (See Figure 9.4 for inclusion of DonorG and DonorT into the model)
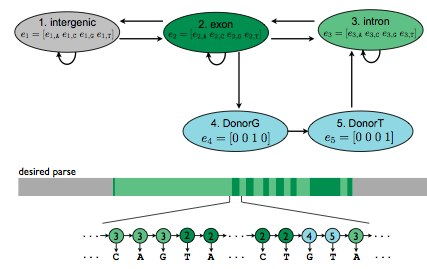
Figure 9.4: Hidden Markov Model Utilizing GT Donor Assumption
The e in each state represents emission probabilities and the arrows indicate the transition probabilities.
Aside from the initial assumptions, additional evidence such as evolutionary conservation and experi- mental mRNA data can help create an HMM to better model the behavior. (See Figure 9.5)

Figure 9.5: Multiple lines of evidence for gene identification
Combining all the lines of evidence discussed above, we can create an HMM with composite emissions in that each emitted value is a “tuple” of collected values. (See Figure 9.6)
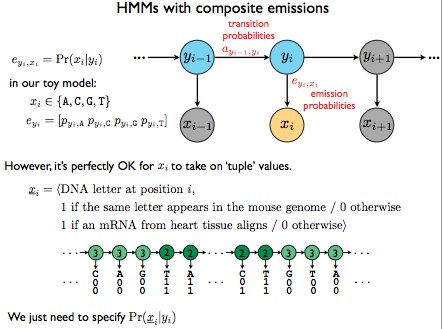
Figure 9.6: HMMs with composite emissions
A few assumptions of this composite model are that each new emission “feature” is independent of the rest. However, this creates the problem that with each new feature, the tuple increases in length, and the number of states of the HMM increases exponentially, leading to a combinatorial explosion, which thus means poor scaling. (Examples of more complex HMMs that can result in poor scaling can be found in Figure 9.7)
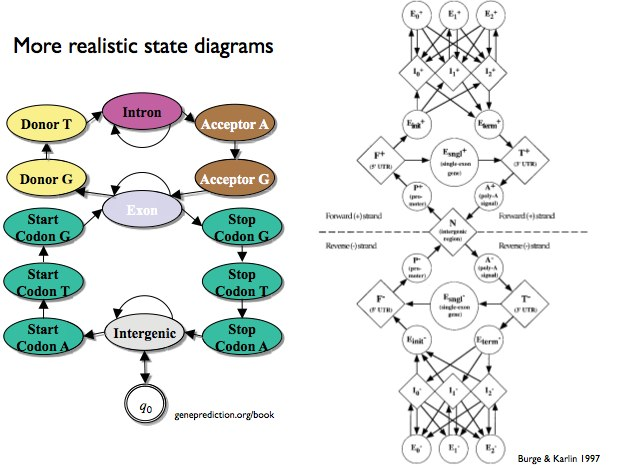
Figure 9.7: State diagram that considers direction of RNA translation


