Skip to main content
Biology LibreTexts

9.6: Conditional Random Fields

  1. Last updated
  2. Save as PDF
  • Page ID
    40971

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Conditional Random Fields, CRFs, are an alternative to HMMs. Being a discriminative approach, this type of model doesnt take into account the joint distribution of everything, as does a poorly scaling HMM. The hidden states in a CRF are conditioned on the input sequence. (See Figure 9.8)3

    page188image51472752.png
    © source unknown. All rights reserved. This content is excluded from our Creative Commons license. For more information, see http://ocw.mit.edu/help/faq-fair-use/.

    Figure 9.8: Conditional random fields: a discriminative approach conditioned on the input sequence

    A feature function is like a score, returning a real-valued number as a function of its inputs that reflects the evidence for a label at a particular position. (See Figure 9.9) The conditional probability of the emitted sequence is its score divided by the total score of the hidden state. (See Figure 9.10)

    page188image51765376.png
    Figure 9.9: Examples of feature functions
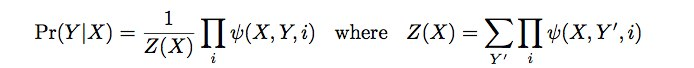
    page188image51763712.png
    Figure 9.10: Conditional probability score of an emitted sequence

    Each feature function is weighted, so that during the training, the weights can be set accordingly.

    The feature functions can incorporate vast amounts of evidence without the Naive Bayes assumption of independence, making them both scalable and accurate. However, training is much more difficult with CRFs than HMMs.

    3Conditional Random Field. Wikipedia. http://en.Wikipedia.org/wiki/Conditional random field

    This page titled 9.6: Conditional Random Fields is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Manolis Kellis et al. (MIT OpenCourseWare) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.