3.6: Pre-processing for linear-time string matching
- Page ID
- 40925
The hashing technique at the core of the BLAST algorithm is a powerful way of string for rapid lookup. A substantial time is invested to process the whole genome, or a large set of genomes, in advance of obtaining a query sequence. Once the query sequence is obtained, it can be similarly processed and its parts searched against the indexed database in linear time.
In this section, we briefly describe four additional ways of pre-processing a database for rapid string lookup, each of which has both practical and theoretical importance.
Suffix Trees
Suffix trees provide a powerful tree representation of substrings of a target sequence T, by capturing all suffixes of T in a radix tree.
Representation of a sequence in a suffix tree
Searching a new sequence against a suffix tree
Linear-time construction of suffix trees
Suffix Arrays
For many genomic applications, suffix trees are too expensive to store in memory, and more efficient rep- resentations were needed. Suffix arrays were developed specifically to reduce the memory consumption of suffix trees, and achieve the same goals with a significantly reduced space need.
Using suffix arrays, any substring can be found by doing a binary search on the ordered list of suffixes. By thus exploring the prefix of every suffix, we end up searching all substrings.
The Burrows-Wheeler Transform
An even more efficient representation than suffix trees is given by the Burrows-Wheeler Transform (BWT), which enables storing the entire hashed string in the same number of characters as the original string (and even more compactly, as it contains frequent homopolymer runs of characters that can be more easily compresed). This has helped make programs that can run even more efficiently.
We first consider the BWT matrix, which is an extension of a suffix array, in that it contains not only all suffixes in sorted (lexicographic) order, but it appends to each suffix starting at position i the prefix ending at position i − 1, each row thus containing a full rotation of the original string. This enables all the suffix-array and suffix-tree operations, of finding the position of suffixes in time linear in the query string.
The key difference from Suffix Arrays is space usage, where instead of storing all suffixes in memory, which even for suffix arrays is very expensive, only the last column of the BWT matrix is stored, based on which the original matrix can be recovered.
An auxiliary array can be used to speed things even further and avoid having to repeat operations of finding the first occurrence of each character in the modified suffix array.
Lastly, once the positions of 100,000s of substrings are found in the modified string (the last column of the BTW matrix), these coordinates can be transformed to the original positions, saving runtime by amortizing the cost of the transformation across the many many reads.
The BWT has had a very strong impact on short-string matching algorithms, and nearly all the fastest read mappers are currently based on the Burrows-Wheeler Transform.
Fundamental pre-processing
This is a variation of processing that has theoretical interest but has found relatively little practical use in bioinformatics. It relies on the Z vector, that contains at each position i the length of the longest prefix of a string that also matches the substring starting at i. This enables computing the L and R (Left and Right) vectors that denote the end of the longest duplicate substrings that contains the current position i.
Educated String Matching
The Z algorithm enables an easy computation of both the Boyer-Moore and the Knuth-Morris-Pratt algorithms for linear-time string matching. These algorithms use information gathered at every comparison when matching strings to improve string matching to O(n). The naive algorithm is as follows: it compares its string of length m character by character to the sequence. After comparing the entire string, if there are any mismatches, it moves to the next index and tries again. This completes in \( O(m ∗ n) \) time.
One improvement to this algorithm is to discontinue the current comparison if a mismatch is found. However, this still completes in \( O(m ∗ n) \) time when the string we are comparing matches the entire sequence.
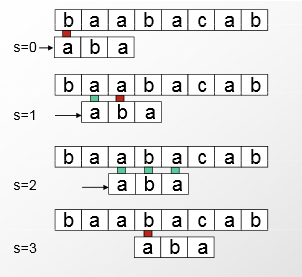
The key insight comes from learning from the internal redundancy in the string to compare, and using that to make bigger shifts down the target sequence. When a mistake is made, all bases in the current comparison can be used to move the frame considered for the next comparison further down. As seen below, this greatly reduces the number of comparisons required, decreasing runtime to \( O(n) \).

© source unknown. All rights reserved. This content is excluded from our Creative Commons license. For more information, see http://ocw.mit.edu/help/faq-fair-use/.


