3.7: Probabilistic Foundations of Sequence Alignment

Last updated
Save as PDF

Page ID: 40926

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

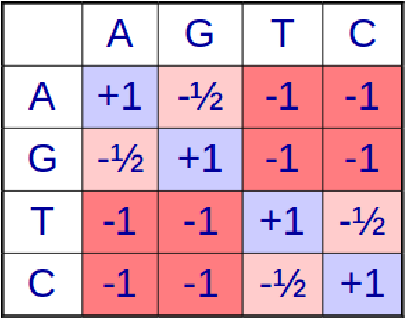
As described above, the BLAST algorithm uses a scoring (substitution) matrix to expand the list of W -mers in order to look for and determine an approximately matching sequence during seed extension. Also, a scoring matrix is used in evaluating matches or mismatches in the alignment algorithms. But how do we construct this matrix in the first place? How do you determine the value of \( s\left(x_{i}, y_{j}\right) \) in global/local alignment?

The idea behind the scoring matrix is that the score of alignment should reflect the probability that two similar sequences are homologous i.e. the probability that two sequences that have a bunch of nucleotides in common also share a common ancestry. For this, we look at the likelihood ratios between two hypotheses.

1. Hypothesis 1: – That the alignment between the two sequence is due to chance and the sequences are, in fact, unrelated.

2. Hypothesis 2: – That the alignment is due to common ancestry and the sequences are actually related.

Then, we calculate the probability of observing an alignment according to each hypothesis. Pr(x, y|U ) is the probability of aligning x with y assuming they are unrelated, while Pr(x,y|R) is the probability of the

alignment, assuming they are related. Then, we define the alignment score as the log of the likelihood ratio between the two:

\[\begin{equation}
S \equiv \log \frac{P(\mathbf{x}, \mathbf{y} \mid R)}{P(\mathbf{x}, \mathbf{y} \mid U)}
\end{equation} \nonumber \]

Since a sum of logs is a log of products, we can get the total score of the alignment by adding up the scores of the individual alignments. This gives us the probability of the whole alignment, assuming each individual alignment is independent. Thus, an additive matrix score exactly gives us the probability that the two sequences are related, and the alignment is not due to chance. More formally, considering the case of aligning proteins, for unrelated sequences, the probability of having an n-residue alignment between x and y is a simple product of the probabilities of the individual sequences since the residue pairings are independent.

That is,

\[ \begin{equation}
\begin{aligned}
\mathbf{x} &=\left\{x_{1} \ldots x_{n}\right\} \\
\mathbf{y} &=\left\{y_{1} \ldots x_{n}\right\} \\
q_{a} &=P(\text { amino acid } a) \\
P(\mathbf{x}, \mathbf{y} \mid U) &=\prod_{i=1}^{n} q_{x_{i}} \prod_{i=1}^{n} q_{y_{i}}
\end{aligned}
\end{equation} \nonumber \]

For related sequences, the residue pairings are no longer independent so we must use a different joint

probability, assuming that each pair of aligned amino acids evolved from a common ancestor:

\[ \begin{equation}
\begin{aligned}
p_{a b} &=P(\text { evolution gave rise to } a \text { in } \mathbf{x} \text { and } b \text { in } \mathbf{y}) \\
P(\mathbf{x}, \mathbf{y} \mid R) &=\prod_{i=1}^{n} p_{x_{i} y_{i}}
\end{aligned}
\end{equation} \nonumber \]

Then, the likelihood ratio between the two is given by:

\[\begin{equation}
\begin{aligned}
\frac{P(\mathbf{x}, \mathbf{y} \mid R)}{P(\mathbf{x}, \mathbf{y} \mid U)} &=\frac{\prod_{i=1}^{n} p_{x_{i} y_{i}}}{\prod_{i=1}^{n} q_{x_{i}} \prod_{i=1}^{n} q_{y_{i}}} \\
&=\frac{\prod_{i=1}^{n} p_{x_{i} y_{i}}}{\prod_{i=1}^{n} q_{x_{i}} q_{y_{i}}}
\end{aligned}
\end{equation} \nonumber \]

Since we eventually want to compute a sum of scores and probabilities require add products, we take the log of the product to get a handy summation:

\[ \begin{equation}
\begin{aligned}
S & \equiv \log \frac{P(\mathbf{x}, \mathbf{y} \mid R)}{P(\mathbf{x}, \mathbf{y} \mid U)} \\
v &=\sum_{i} \log \left(\frac{p_{x_{i} y_{i}}}{q_{x_{i}} q_{y_{i}}}\right) \\
& \equiv \sum_{i} s\left(x_{i}, y_{i}\right)
\end{aligned}
\end{equation} \nonumber \]

Thus, the substitution matrix score for a given pair a, b is give by

\[ \begin{equation}
s(a, b)=\log \left(\frac{p_{a b}}{q_{a} q_{b}}\right)
\end{equation} \nonumber \]

The above expression is then used to crank out a substitution matrix like the BLOSUM62 for amino acids. It is interesting to note that the score of a match of an amino acid with itself depends on the amino acid itself because the frequency of random occurrence of an amino acid affects the terms used in calculating the likelihood ratio score of alignment. Hence, these matrices capture not only the sequence similarity of the alignments, but also the chemical similarity of various amino acids.

© source unknown. All rights reserved. This content is excluded from our Creative Commons license. For more information, see http://ocw.mit.edu/help/faq-fair-use/.
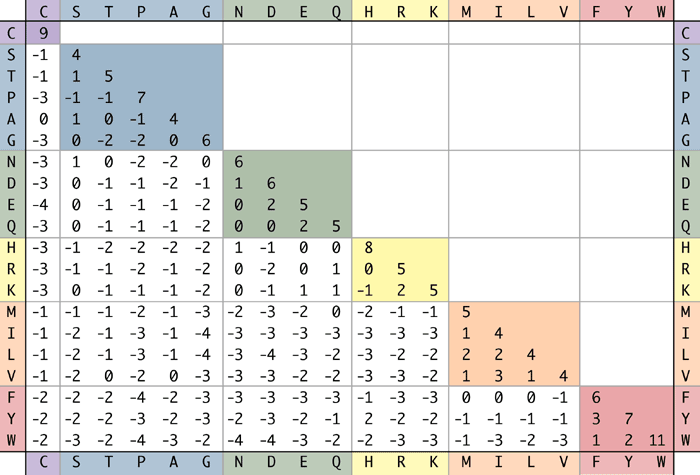
Figure 3.17: BLOSUM62 matrix for amino acids