3.5: The BLAST algorithm (Basic Local Alignment Search Tool)
- Page ID
- 40924
The BLAST algorithm looks at the problem of sequence database search, wherein we have a query, which is a new sequence, and a target, which is a set of many old sequences, and we are interested in knowing which (if any) of the target sequences is the query related to. One of the key ideas of BLAST is that it does not require the individual alignments to be perfect; once an initial match is identified, we can fine-tune the matches later to find a good alignment which meets a threshold score. Also, BLAST exploits a distinct characteristic of database search problems: most target sequences will be completely unrelated to the query sequence, and very few sequences will match.
However, correct (near perfect) alignments will have long substrings of nucleotides that match perfectly. E.g. if we looking for sequences of length 100 and are going to reject matches that are less than 90% identical, we need not look at sequences that do not even contain a consecutive stretch of less than 10 matching nucleotides in a row. We base this assumption on the : if m items are put in n containers and m>n, at least 2 items must be put in one of the n containers.

Figure 3.12: Pigeonhole Principle
In addition, in biology, functional DNA is more likely to be conserved, and therefore the mutations that we find will not actually be distributed randomly, but will be clustered in nonfunctional regions of DNA while leaving long stretches of functional DNA untouched. Therefore because of the pigeonhole principle and because highly similar sequences will have stretches of similarity, we can pre-screen the sequences for common long stretches. This idea is used in BLAST by breaking up the query sequence into W-mers and pre-screening the target sequences for all possible \( W − mers \)by limiting our seeds to be \( W − mers \)in the neighborhood that meet a certain threshold.
The other aspect of BLAST that allows us to speed up repeated queries is the ability to preprocess a large database of DNA off-line. After preprocessing, searching for a sequence of length m in a database of length n will take only O(m) time. The key insights that BLAST is based on are the ideas of hashing and neighborhood search that allows one to search for W − mers, even when there are no exact-matches.
The BLAST algorithm
The steps are as follows:
- Split query into overlapping words of length W (the W-mers)
- Find a “neighborhood” of similar words for each word (see below)
- Lookup each word in teh neighborhood in a hash table to find the location in the database where each word occurs. Call these the seeds, and let S be the collection of seeds.
- Extend the seeds in S until the score of the alignment drops off below some threshold X.
- Report matches with overall highest scores
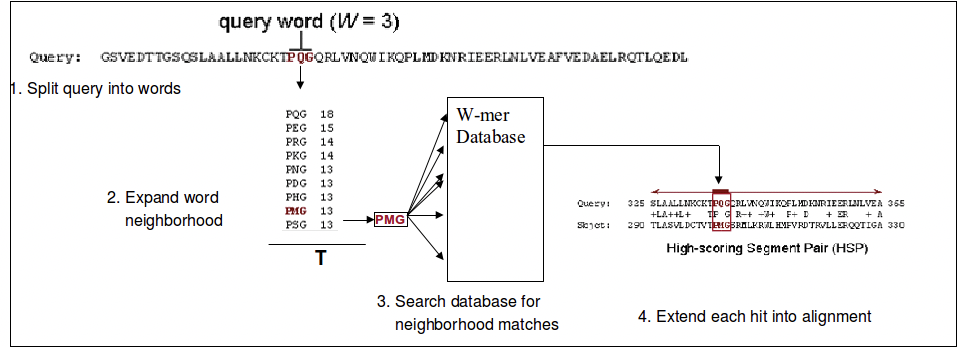
Figure 3.13: The BLAST Algorithm
The pre-processing step of BLAST makes sure that all substrings of W nucleotides will be included in our database (or in a hash table). These are called the W -mers of the database. As in step 1, we first split the query by looking at all substrings of W consecutive nucleotides in the query. To find the neighborhood of these W-mers, we then modify these sequences by changing them slightly and computing their similarity to the original sequence. We generate progressively more dissimilar words in our neighborhood until our similarity measure drops below some threshold T. This affords us flexibility to find matches that do not have exactly W consecutive matching characters in a row, but which do have enough matches to be considered similar, i.e. to meet a certiain threshold score.
Then, we look up all of these words in our hash table to find seeds of W consecutive matching nucleotides. We then extend these seeds to find our alignment using the Smith-Waterman algorithm for local alignment, until the score drops below a certain threshold X. Since the region we are considering is a much shorter segment, this will not be as slow as running the algorithm on the entire DNA database.
It is also interesting to note the influence of various parameters of BLAST on the performance of the algorithm vis-a-vis run-time and sensitivity:
- W Although large W would result in fewer spurious hits/collisions, thus making it faster, there are also tradeoffs associated, namely: a large neighborhood of slightly different query sequences, a large hash table, and too few hits. On the other hand, if W is too small, we may get too many hits which pushes runtime costs to the seed extension/alignment step.
- T If T is higher, the algorithm will be faster, but you may miss sequences that are more evolutionarily distant. If comparing two related species, you can probably set a higher T since you expect to find more matches between sequences that are quite similar.
- X Its influence is quite similar to T in that both will control the sensitivity of the algorithm. While W and T affect the total number of hits one gets, and hence affect the runtime of the algorithm dramatically, setting a really stringent X despite less stringent W and T, will result runtime costs from trying unnecessary sequences that would not meet the stringency of X. So, it is important to match the stringency of X with that of W and T to avoid unnecessary computation time.
Extensions to BLAST
• Filtering Low complexity regions can cause spurious hits. For instance, if our query has a string of copies of the same nucleotide e.g. repeats of AC or just G, and the database has a long stretch of the same nucleotide, then there will be many many useless hits. To prevent this, we can either try to filter out low complexity portions of the query or we can ignore unreasonably over-represented portions of the database.
• Two-hit BLAST The idea here is to use double hashing wherein instead of hashing one long W -mer, we will hash two small W-mers. This allows us to find small regions of similarity since it is much more likely to have two smaller W-mers that match rather than one long W-mer. This allows us to get a higher sensitivity with a smaller W, while still pruning out spurious hits. This means that we’ll spend less time trying to extend matches that don’t actually match. Thus, this allows us to improve speed while maintaining sensitivity.
Q: For a long enough W, would it make sense to consider more than 2 smaller W-mers?
A: It would be interesting to see how the number of such W-mers influences the sensitivity of the algorithm. This is similar to using a comb, described next.
• Combs This is the idea of using non-consecutive W-mers for hashing. Recall from your biology classes that the third nucleotide in a triplet usually doesnt actually have an effect on which amino acid is represented. This means that each third nucleotide in a sequence is less likely to be preserved by evolution, since it often doesnt matter. Thus, we might want to look for W-mers that look similar except in every third codon. This is a particular example of a comb. A comb is simply a bit mask which represents which nucleotides we care about when trying to find matches. We explained above why 110110110 . . . (ignoring every third nucleotide) might be a good comb, and it turns out to be. However, other combs are also useful. One way to choose a comb is to just pick some nucleotides at random. Rather than picking just one comb for a projection, it is possible to randomly pick a set of such combs and project the W-mers along each of these combs to get a set of lookup databases. Then, the query string can also be projected randomly along these combs to lookup in these databases, thereby increasing the probability of finding a match. This is called Random Projection. Extending this, an interesting idea for a final project is to think of different techniques of projection or hashing that make sense biologically. One addition to this technique is to analyze false negatives and false positives, and change the comb to be more selective. Some papers that explore additions to this search include Califino-Rigoutsos’93, Buhler’01, and Indyk-Motwani’98.
• PSI-BLAST Position-Specific Iterative BLAST create summary profiles of related proteins using BLAST. After a round of BLAST, it updates the score matrix from the multiple alignment, and then runs subsequent rounds of BLAST, iteratively updating the score matrix. It builds a Hidden Markov Model to track conservation of specific amino acids. PSI-BLAST allows detection of distantly-related proteins.


