3.1.1: Introduction to Cells

Figure \(\PageIndex{1}\):(a) onion cells, and (b) Elodea cells, both viewed with a light microscope. Credit: Kammy Algiers (CC-BY).

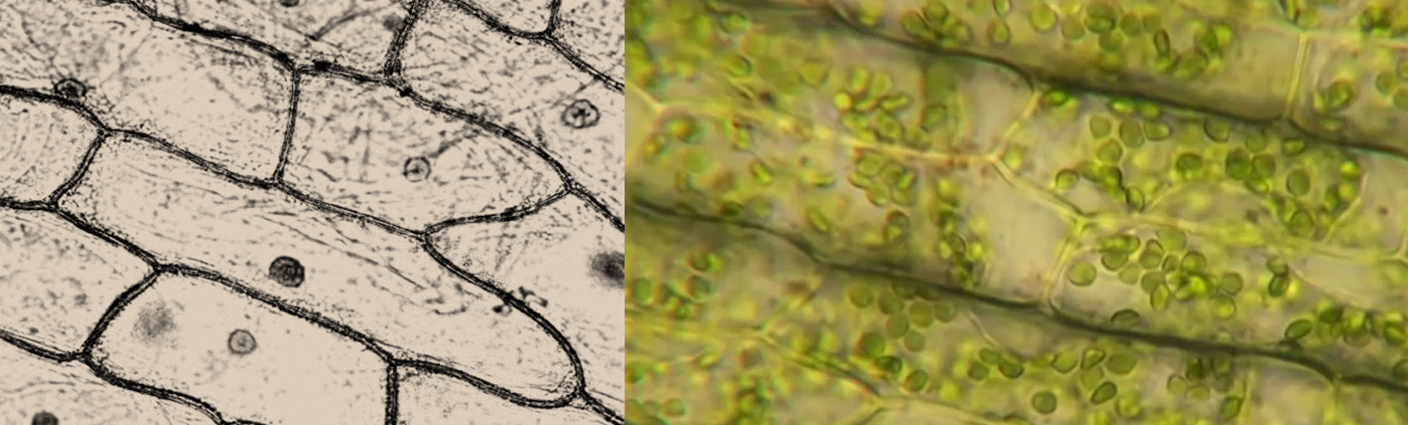
Learning Objectives

• Describe the role of cells in organisms.
• Summarize cell theory.
• Address the significance of cell size.

A cell is the smallest unit of a living thing. Whether comprised of one cell (like bacteria) or many cells (like a plant, Figure \(\PageIndex{1}\)), we call it an organism. Thus, cells are the basic building blocks of all organisms.

Several plant cells of one kind that interconnect with each other and perform a shared function form tissues. An example of a plant tissue would be the epithelial tissue found on the surface of a leaf. These tissues combine to form an organ, such as a leaf. and several organs comprise an organ system (in this case, the shoot system). Two two plant organ systems, the shoot and root system, make up the plant. Here, we will examine the structure and function of cells.

Cell Theory

In 1665, Robert Hooke looked at cork under a microscope and saw multiple chambers which he called “cells”. In 1838, Schleidern and Schwann stated that (1) all plants and animals are composed of cells and that (2) cell is the most basic unit (“atom”) of life. In 1858, Virchow stated that (3) all cells arise by reproduction from previous cells (“Omnis cellula e cellula” in Latin). These three statements became the base of the cell theory.

Cell Size

At 0.1 to 5.0 μm in diameter, prokaryotic cells are significantly smaller than eukaryotic cells, which have diameters ranging from 10 to 100 μm (Figure \(\PageIndex{2}\). The prokaryotes' small size allows ions and organic molecules that enter them to quickly diffuse to other parts of the cell. Similarly, any wastes produced within a prokaryotic cell can quickly diffuse. This is not the case in eukaryotic cells, which have developed different structural adaptations to enhance intracellular transport.

Figure \(\PageIndex{2}\)): This figure shows relative sizes of microbes on a logarithmic scale (recall that each unit of increase in a logarithmic scale represents a 10-fold increase in the quantity measured). Note that the smallest object is an atom, about 1 nm in size while the largest is a human, at approximately 1m tall.

Small size, in general, is necessary for all cells, whether prokaryotic or eukaryotic. Let’s examine why that is so. First, we’ll consider the area and volume of a typical cell. Not all cells are spherical in shape, but most tend to approximate a sphere. You may remember from your high school geometry course that the formula for the surface area of a sphere is 4πr², while the formula for its volume is 4πr³/3. Thus, as the radius of a cell increases, its surface area increases as the square of its radius, but its volume increases as the cube of its radius (much more rapidly). Therefore, as a cell increases in size, its surface area-to-volume ratio decreases. This same principle would apply if the cell had a cube shape (Figure \(\PageIndex{3}\)). If the cell grows too large, the plasma membrane will not have sufficient surface area to support the rate of diffusion required for the increased volume. In other words, as a cell grows, it becomes less efficient. One way to become more efficient is to divide. Other ways are to increase surface area by foldings of the cell membrane, become flat or thin and elongated, or develop organelles that perform specific tasks. These adaptations lead to developing more sophisticated cells, which we call eukaryotic cells.

Visual connection

(Figure \(\PageIndex{3}\)): Notice that as a cell increases in size, its surface area-to-volume ratio decreases. When there is insufficient surface area to support a cell’s increasing volume, a cell will either divide or die. The cell on the left has a volume of 1 mm³ and a surface area of 6 mm², with a surface area-to-volume ratio of 6 to 1; whereas, the cell on the right has a volume of 8 mm³ and a surface area of 24 mm², with a surface area-to-volume ratio of 3 to 1.

Attributions

Curate and authored by Kammy Algiers using the following sources:

• 4.1 Studying Cells from Biology2e by OpenStax (licensed CC-BY). Access for free at openstax.org.
• 2.1 Introduction to Cells from Introduction to Botany by Alexey Shipunov (public domain)