2.4: Using Topographic Slope to Determine Tree Height
- Page ID
- 20250
For most natural resources management purposes, land areas and distances are measured in English units. (Research data are collected in metric units.) Therefore, we measure area in acres, tree height in feet, and commonly, horizontal distance in chains (1 chain = 66 ft.). For this reason, many instruments for measuring slope have two scales: %slope and topographic slope. Topographic slope (or Tslope) is essentially the same as %slope, except that instead of expressing the ratio of rise over run as a proportion of 1:100, Tslope is expressed in a proportion of 1:66 as follows:
\[\left(\frac{rise}{run}\right)(66)=\text { Tslope }\]
The different multiplier (66) is the only difference between Tslope and %slope. To solve the Tslope equation for “rise” we do the following:
- Multiply both sides of the equation by “run” to cancel out run on the left side of the equation \[\frac{(r u n)(r i s e)(66)}{r u n}=(run)(\text { Tslope })\]
- Divide both sides by “66” to cancel out 66 on the left side of the equation \[\frac{(\text {rise})(66)}{66}=\frac{(r u n)}{66}(\text { Tslope })\]
That leaves us with the following equation:
\[rise=\frac{(run)}{66}(\text { Tslope })\]
where \(rise =height\)
So, just as with %slope, the Tslope multiplier (66) becomes the denominator.
Topographic slope is most commonly used when measuring merchantable height, but is also fine for measuring total height on shorter trees. Here is an example (Figure 2.7):
Example \(\PageIndex{1}\)
If Jake walks out a horizontal distance of 66 feet (one chain) from the tree, his run will equal the \(Tslope\) multiplier. The “66” will cancel out, and he can simply add his top and stump slope readings together.
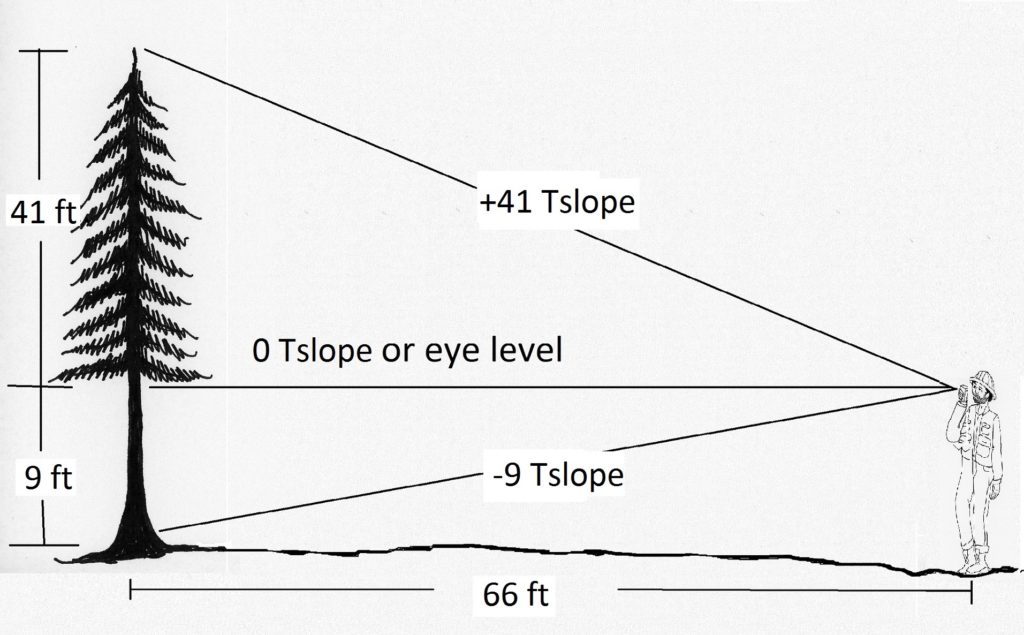
Solution
\[rise=\frac{(run)}{66}\left(T_{\text {slape }}\right)\]
\[rise=\frac{(66)}{66}(41+9)\]
\[\text { rise (height) }=50 \text { feet. }\]


