6.1: How Enzymes Work
- Page ID
- 14949
In this section, we will explore chemical and physical factors that speed up reactions, and begin to relate these effects to reactions catalyzed by enzymes. We will see that enzymes employ various chemical strategies to increase the rates of reactions, in addition to physical ones like reactant proximity and the introduction of strain. This can result in reactions that are 10 million (or more!) times faster than the uncatalyzed reaction. To put this 10 million-fold rate enhancement in perspective, if the catalyzed reaction takes one second, the uncatalyzed one would take nearly four months!
This chapter section has been written by Kristen Procko and Henry Jakubowski.
Reactions in solution that are not catalyzed are slow. Consider the hydrolysis of an ester in water, illustrated in Figure \(\PageIndex{1}\). The ester is stabilized by resonance, and is therefore weakly electrophilic; thus, attack by weakly nucleophilic water is a slow process. Examining the transition state, we can see that charge development and separation occurs in the transition state for the uncatalyzed reaction, resulting in an intermediate (P) with both positive and negative charges.
Figure \(\PageIndex{1}\): Charge development in the transition state during ester hydrolysis
When bonds are made or broken, charged intermediates are often formed, which are higher in energy than the reactants. Consider the energy diagram for the first step of a generic endergonic reaction, shown in \(\PageIndex{2}\). The transition state is closer in energy to the intermediae P, than it is to the reactant R. Therefore, the TS more closely resembles P than it does the starting reactants. Applying this analysis to the ester hydrolysis reaction from Figure \(\PageIndex{1}\), the transition state is closer in energy to the charge-separated intermediate P, and therefore more closely resembles the charge-separated species. In this example, the intermediate is higher in energy than the reactants, thus the transition state is even higher in energy than the intermediate.

Figure \(\PageIndex{2}\): An energy diagram for an endergonic reaction (Image modified from: Chemistry LibreTexts, 6.9)
Anything that can stabilize the charges on the intermediate will also stabilize the developing charges in the transition state. This lowers the energy of the transition state and catalyzes the reaction. In this section, we will investigate the mechanism underlying the catalysis by small molecules of chemical reactions. Presumably, biological macromolecular catalysts (like protein enzymes) will use similar mechanisms in their catalytic effects (which will be discussed in the next section).
Catalysts, including enzymes, can employ at least 5 different ways to stabilize transition states.
Chemical Strategies for Rate Enhancement
General Acid and Base Catalysis
Considering intermediate P in Figure \(\PageIndex{1}\), we can envision two strategies to reduce the charge separation: the negative charge on the anionic oxygen could be protonated, or the positive charge on the cationic oxygen could be removed by deprotonation. If the reaction is pH dependent, and the reaction rate solely depends on hydronium ion concentration, [H3O+], then specific acid catalysis is operative. Specific acid catalysis occurs when the hydronium ion concentration is the sole factor determining the reaction rate, and the rate is not influenced by the concentration of any buffer components present in the solution. In other words, the rate of the reaction depends specifically on the concentration of hydronium ion. Specific base catalysis occurs when the reaction rate is dependent solely on the concentration of hydroxide ion, and is again independent of any buffer components in solution.
By contrast, general acid catalysis occurs when the reaction is not solely dependent on the [H3O+] concentration; that is, the reaction rate is influenced by the concentration of a buffer component. With general acid catalysis, the charge separation in the transition state is decreased by donation of a proton to the carbonyl from general acids (e.g., acetic acid or a protonated imidazole ring). Proton donation decreases the developing negative in the transition state. In Figure \(\PageIndex{3}\), the first step of the ester hydrolysis mechanism is shown via specific acid catalysis, alongside the general acid catalysis mechanism using the weak acid, acetic acid.
Figure \(\PageIndex{3}\): Specific vs. general acid catalysis
Alternatively, the first step of the ester hydrolysis mechanism can be base-catalyzed, which increases the strength of the nucleophile. In Figure \(\PageIndex{1}\), the attacking water molecule develops a partial positive charge in the transition state as it begins to form a bond to the electrophilic carbon of the carbonyl. In the base-catalyzed mechanism shown in Figure \(\PageIndex{4}\), hydroxide becomes the nucleophile in the specific base-catalyzed mechanism. The energy of the transition state can also be lowered by the presence of a general base (e.g., acetate, a deprotonated imidazole ring). Proton abstraction decreases the developing positive charge.
Figure \(\PageIndex{4}\): Specific vs. general base catalysis
General acid/base catalysis is common with enzymes because enzymes often use amino acid side chains to promote acid-base reactions within the active site, the region of the enzyme where the chemical reaction takes place. Acetic acid is similar to glutamic and aspartic acid side chains, and the imidazole ring shown in the general base catalysis reaction in Figure \(\PageIndex{4}\) is present in the side chain of the amino acid histidine.
Metal Ion or Electrostatic Catalysis
A metal such as Cu2+ or Zn2+ can also stabilize the transition state. The metal must be able to bind the charged intermediate and hence the transition state. An oxyanion intermediate formed during the reaction of an electrophilic carbonyl C can interact with a metal, especially when there is an O on an adjacent atom which can help coordinate the metal ion. This charge stabilization of the developing negative in the transition state and the full negative in the intermediate is often called electrostatic catalysis, and is illustrated in the decarboxylation of a β-keto carboxylic acid Figure \(\PageIndex{5}\). Coordination of Cu2+ to the β-keto carboxylic acid increases the electrophilicity of the carbonyl, making it a superior electron acceptor, which facilitates decarboxylation. The intermediate enolate formed in the decarboxylation is protonated, giving the more stable ketone as the product.
Figure \(\PageIndex{5}\): Metal ion catalysis
Electrostatic catalysis is likely to occur in many enzymes since nearly 1/3 of all enzymes require metal ions. A classic example of an enzyme using metal ion catalysis is carboxypeptidase A. Figure \(\PageIndex{6}\)s shows an interactive iCn3D model of Zn and the inhibitor citric acid bound to carboxypeptidase A (3KGQ). Note the histidine and aspartate amino acid side chains of the active site coordinating to the Zn2+ ion, along with the carboxylate group of citrate.
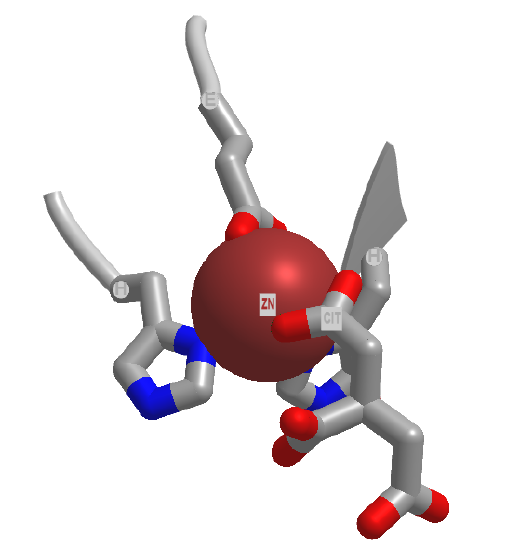
Metals can also act in a different way. They may coordinate a water and by further polarizing the H-O bond increase the acidity of the bound water. For instance, a water molecule in the hexaaquairon(III) ion has a pKa of 9.4, compared to pure water, with a pKa of 14 (\(\PageIndex{7}\)). The complexed hydroxide is a better nucleophile than bulk water.
Figure \(\PageIndex{7}\): Metal ion decrease of pKa of coordinated water
Another enzyme that utilizes Zn2+ is carbonic anhydrase. It is among the fastest of all enzymes, with a kcat of 106 s-1 and a kcat/Km of 8.3 x 107 M-1s-1 (reference). It is diffusion controlled at low substrate (CO2) concentration and converts one million bound CO2 per second to HCO3-! The Zn2+ appears to bind a water molecule and reduce its pKa such that the bound form is OH-. This is illustrated in Figure \(\PageIndex{8}\), which depicts the local environment of the bound Zn2+ (coordinated by 3 histidine side chains and an OH-) in the absence (left) and presence (right) of CO2.
Covalent or Nucleophilic Catalysis
One way to change the activation energy of the reaction is to change the reaction mechanism in ways which introduces new steps with lower activation energy. As shown in Figure \(\PageIndex{9}\), the catalyzed reaction has a new lower energy well, representing formation of the covalent intermediate, and the activation energy is lowered overall. Formation of the new intermediate results in two transition states, represented by the two high energy points of the blue line in the plot.
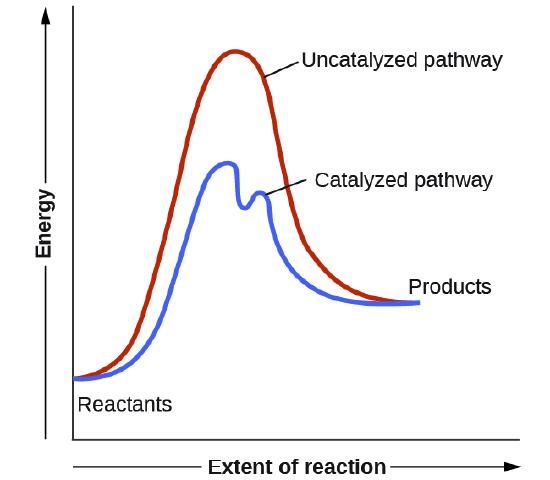
Figure \(\PageIndex{9}\): Energy diagram for an uncatalyzed reaction compared to a catalyzed reaction that utilizes covalent catalysis.
A typical way to achieve covalent catalysis is to add a nucleophilic catalyst, which forms a covalent intermediate with the reactant. Figure \(\PageIndex{8}\) shows how pyridine (red) acts as a nucleophilic or covalent catalyst in the hydrolysis of an anhydride. The anhydride is very reactive to start with, and the charged pyridinium ion intermediate contains a very good leaving group. The desired nucleophile, water, can then interact with the intermediate in a nucleophilic substitution reaction. In these types of reactions in general, as long as the nucleophilic catalyst is a better nucleophile than the ultimate nucleophile (usually water) then the activation energy is lowered, and the reaction is catalyzed. The nucleophilic catalyst and the original nucleophile usually interact with a carbonyl C in a substitution reaction.
Figure \(\PageIndex{10}\): Nucleophilic covalent catalysis by pyridine
Reactions involving iminium ions are a recurring theme in biochemistry
Positively-charged nitrogen cations (iminium ions) form as intermediates in many biochemical mechanisms. The iminium ion is a powerful electron acceptor, and can promote the cleavage of bonds that would otherwise be difficult to break, such as C–C and C–H bonds. To begin our analysis of how iminium ions promote such cleavage reactions, let's revisit a common carbon-carbon bond cleaving reaction, the decarboxylation of a β-keto acid, which we examined briefly above in Figure \(\PageIndex{5}\) with metal ion catalysis.
Under acidic conditions, β-keto acids usually decarboxylate with gentle warming. A cyclic transition state is often invoked, and the presence of the carbonyl of the ketone, adjacent to the breaking bond, gives the electrons somewhere to go (Figure \(\PageIndex{11}\)). The product of the decarboxylation is an enol, which tautomerizes to the more stable ketone. Under the slightly basic conditions that characterize the medium for most biochemical reactions, the equilibrium favors the deprotonated carboxylate form. The adjacent carbonyl again gives the electrons somewhere to go in the decarboxylation reaction, and under these basic conditions, an enolate is formed. Protonation gives the final product, a ketone.
Figure \(\PageIndex{11}\): Decarboxylation of a β-keto acid under acidic conditions, and at pH 7.4
In Figure \(\PageIndex{5}\), we saw that a metal ion can promote the decarboxylation reaction by interacting with the electron-accepting ketone carbonyl, which makes it even more electrophilic. Another strategy to create a better electron acceptor involves forming a full positive charge on the electron accepting atom, which can be done by converting the ketone to an iminium ion. Amines react with aldehydes or ketones to form iminium ions. Figure \(\PageIndex{12}\) illustrates this strategy, which involves covalent catalysis. The amine, RNH2, reacts to form a new intermediate, the iminium ion, with a full positive charge. The protonated nitrogen serves as an excellent electron "sink" for decarboxylation reactions of beta-keto acids.
This iminium ion or protonated Schiff Basehas a pKa of about 7, so the protonated iminium and deprotonated imine are in equilibrium near pH 7. Figure \(\PageIndex{12}\) also illustrates a simple way to view reaction mechanisms. Electrons in chemical reactions can be viewed as flowing from a source (such as a carboxyl group) to a sink (such as an electrophilic carbonyl O or a positively charged N in a Schiff base).
Acid- and base-catalyzed reaction mechanisms for Schiff base formation are shown in Figure \(\PageIndex{13}\). An amine is used as the nucleophilic catalyst, forming the initial addition product, a carbinolamine. The carbinolamine dehydrates, since the free pair of electrons on the N are more likely to be shared with the carbon to form a double bond than electrons from the original carbonyl O, which is more electronegative than the N. If catalyzed by a general acid, an iminium ion, and the base-catalyzed reaction forms an imine. Near pH 7.4, the imine easily protonated to form a positively charged N at the former carbonyl O center.
Figure \(\PageIndex{13}\): Schiff Base Formation - reaction mechanism
An actual Schiff base intermediate between fructose-1,6-bisphosphate (2FP-400) and Lys 239 from the enzyme fructose bisphosphate aldolase from Leishmania mexicana is shown in Figure \(\PageIndex{14}\). Only a single bond between the carbon and nitrogen in the Schiff base is shown.
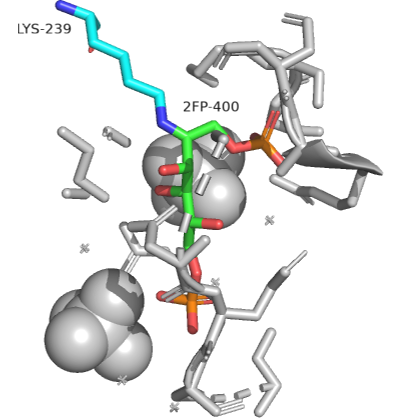
Figure \(\PageIndex{14}\): Schiff base intermediate between fructose-1,6-bisphosphate (2FP-400) and Lys 239 from the enzyme fructose bisphosphate aldolase from Leishmania mexicana(2QDG)
Transition State Stabilization
In the middle of the 20th century, Linus Pauling postulated that the only thing that a catalyst must do is bind the transition state more tightly than the substrate. This can be discerned in Figure \(\PageIndex{15}\) and a little math. The diagram shows how the substrate (S) and the transition state (S*) can react with an enzyme (E) to form a complex which then proceeds to product (following the diagram from "start here" in the right-hand direction), or can go to product in the absence of enzyme (E) (following the diagram from "start here" in the left-hand direction). Note that the diagram is arbitrarily drawn such that the standard Gibbs free energy (G°) of the free product P is higher than that of the free substrate, S.
Figure \(\PageIndex{15}\): Enzymes bind the transition state more tightly than the substrate
The colored large vertical arrows represent the ΔG° for the transition shown:
- The red arrows A and B represent the ΔG°s for the binding of E + S (arrow A) and E + S* (arrow B), respectively.
- The green arrows C and D represent the ΔG°s for the activation energy of the free substrate (arrow C) and the enzyme-bound substrate (arrow D).
Now consider the two pairs of arrows, A,C and D,B and add each set like a vector in elementary physics. Since the distance between the two horizontal blue lines is the same for the left hand process (uncatalyzed) and the right hand one (catalyzed), it follows that
\begin{equation}
C-A=D-B
\end{equation}
The negative signs for A and B are used since in the diagram both A and B have negative ΔG° values.
Now for an enzyme to be a catalyst, the activation energy D for the reaction in the presence of the enzyme E must be less positive (i.e., smaller) than the activation energy C in the absence of enzyme. Therefore, after rearranging the equation:
\begin{equation}
C-D=A-B>0
\end{equation}
and substituting in the ΔG° values for A and B, we can directly compare the free energy of binding the substrate (S) vs. binding the transition state (S*):
\begin{equation}
-R T \ln \mathrm{K}_{\mathrm{eq} \mathrm{S}}-\left(-\mathrm{RT} \ln \mathrm{K}_{\mathrm{eq} \mathrm{S}^{*}}\right)>0
\end{equation}
Hence, the equilibrium constant for binding the transition state is larger than that for binding free substrate:
\begin{equation}
\mathrm{K}_{\text {eq } S^{*}}>\mathrm{K}_{\text {eq } \mathrm{S}}
\end{equation}
Pauling was right. The enzyme just needs to bind the transition state more tightly than the substrate to catalyze the reaction. This is why chemists synthesize stable transition state analogs as potential tight binding inhibitors of target proteins.
The stability of the transition state also affects the reaction kinetics (which makes sense given that the activation energy clearly affects the speed of a reaction). As you probably remember from organic chemistry, biomolecular nucleophilic substitution (SN2) reactions are slow when the central atom where the substitution will occur is surrounded by bulky substituents (sterics once again). We discussed this in context to nucleophilic substitution on a sp2 hybridized carbonyl carbon in carboxylic acid derivatives versus on a sp3 hybridized phosphorous in phosphoesters and diesters. The explanation for this phenomena has usually been attributed to hindered access of the central atom caused by bulky substituents (intrinsic effects). Is this true? Studies on SN2 reactions of methylchloroacetonitrile and t-butylchloroacetonitrile (with the reagent labeled with 35Cl) using 37Cl- as the incoming nucleophile in the gas phase shown that the more hindered t-butyl derivative's activation energy was only 1.6 kcal/mol (6.7 kJ/mol) higher than the methyl derivative, but in aqueous solution, the difference is much greater for comparable reactions (Figure \(\PageIndex{16}\):).
Figure \(\PageIndex{16}\): SN2 reactions are characterized by a pentavalent transition state
They attributed the differences to solvation effects of the transition state. The bulkier the substituents on the central atom, the more difficult it is to solvate the transition state since water can't reorient around it as well. In effect there is steric hindrance for both reactant and solvent.
What does it take for a macromolecule (M) to be a catalyst - an enzyme? It seems the minimum criterion are:
- M binds a reactant
- M binds the transition state more tightly than the substrate
Anything above these is just "icing on the cake". If different functional group are present in the "active" site of the enzyme that would allow electrostatic, intramolecular, covalent, general acid and/or base catalysis, the better the catalyst.
A transition state analog case study: Abyzmes (Antibody Catalysis)
Recall that antibodies are immune system proteins that bind foreign molecules (see Chapter 5.4). The usual role of an antibody is to initiate an immune response. When the antigen-binding site, located in the variable region of an antibody, binds to an antigen, it triggers the formation of new antibodies (within B-cells) in an effort to optimize the immune response to that antigen. These new antibodies are made with mutations in the antigen binding region, and those that bind better than the original antibody will be selected to form longer lived memory B-cells, ready for the next time the body encounters the antigen.
Decades ago, Linus Pauling made a hypothesis that antibodies could be produced with an atypical role—to act as catalysts! If antibody molecules could be made to bind to a compound resembling the transition state of a chemical reaction, they should also presumably catalyze the chemical reaction. In 1987, his prediction was verified. Lerner et al. made a transition state analog of an ester. When an ester is hydrolyzed, as shown in Figure \(\PageIndex{17}\), the sp2 hybridized carbonyl carbon is converted to an sp3 hybridized center in the intermediate, with the carbonyl oxygen becoming an oxyanion.
The transition state presumably looks more like this unstable intermediate (sp3, oxyanion). Thus, Lerner synthesized a phosphonate, an ester mimic with a sp3 hybridized phosphorous replacing the carbonyl C. It also has a negatively charged oxygen as does the intermediate for the ester. This phosphonate ester is very resistant to hydrolysis. When injected into a mouse (after first being covalently attached to a carrier protein so the small molecule becomes "immunogenic"), the mouse makes a protein antibody which binds to the phosphonate. When the corresponding carboxylic acid ester is added to the antibody, it is cleaved with nominal kcat and KM values. Site specific mutagenesis can then be done to make it an even better catalyst! The antibody enzymes have been called abzymes. The structure shown in Figure \(\PageIndex{17}\) shows how phosphonamides act as transition state analogs as well.
Figure \(\PageIndex{17}\): PHOSPHONAMIDES: TRANSITION STATE ANALOGS
Figure \(\PageIndex{18}\)s shows an interactive iCn3D model of transition state analog 5-(para-nitrophenyl phosphonate)-pentanoic acid bound to a mouse Fab antibody fragment with esterase activity (1aj7)
.png?revision=1&size=bestfit&width=269&height=251)
Transition state theory can be used to more clearly quantify the relationships described in the graphical analysis above. This analysis will use the equilibrium constant (in contrast to the last two chapters which used dissociation constants to characterize macromolecule, receptor, and enzyme binding to ligand). Let assume that a substrate S is in equilibrium with its transition state S‡. Hence Keq = [S‡]/[S]. The following reaction can be written: S → S‡ → P. Based on our previous kinetic analysis and experience in writing differential equations, dP/dt = k1[S‡]. By analogy, enzyme bound S (ES) can be converted to (ES‡) and then on to product as shown in the following chemical equation:
\[\ce{E + S <=> ES -> ES^{†} -> E + P}. \nonumber \]
For the non-enzyme catalyzed reaction, transition state theory can be used to show that the first order rate constant k1= kT/h where k is the Boltzman's constant, T is the Kelvin temperature, and h is Planck's constant. Hence, using Keq = [S†]/[S], equation 1 can be derived
\begin{equation}
\frac{d P}{d t}=\frac{k T}{h}\left[S^{\dagger}\right]=\frac{k T}{h} K^{\dagger}[S]=k_{n}[S]
\end{equation}
where kn (hereafter written as kN) =(kT/h)K† is the effective first order rate for the non-catalyzed rate. Now let's create a more complicated linked equilibrium showing the same reaction in the presence of an enzyme. Figure \(\PageIndex{19}\)
Remember that the K values for this analysis are equilibrium constants not dissociation constants. Note two important equilibrium constants, KS, the equilibrium constant for the binding of free S to E, and KT, the equilibrium constant for the binding of free S† to E (assuming that free S† could bind to E before it converted to product). As we have seen for linked equilibrium before, since the Keq values are related to the standard free energy changes which are state functions, the sum of the standard free energies going from E + S to ES† (by either the top or bottom paths) are path independent so the products of the Keq for the top path are equal to those for the bottom paths. This gives the following equation:
\begin{equation}
\frac{K_{T}}{K_{S}}=\frac{K_{E^{\dagger}}}{K_{N^{\dagger}}}=\frac{k_{E}}{k_{N}}
\end{equation}
The right hand side is the ratio of the effective first order rate constant for conversion or ES† → E + P, kE divided by the rate constant for the conversion of S† → P for the noncatalyzed rate, kN. The final ratio of rate constants can be derived from the simple relationship that kx=(kT/h)K†x where x is either N (non catalyzed) or E (enzyme catalyzed). Equation 2 states that the equilibrium constant for the binding of S† to E, KT, is greater than the equilibrium constant for the binding of S to E, KS (as kE > kN). KT/KR ranges from 108 - 1014. Given common values for the equilibrium constant for binding of S to E (103 – 105 M-1) which is equivalent to dissociation constant values Kd = 10 uM – 1 mM, the calculated value of KT = 1015 M-1 which gives a dissociation constant for the enzyme and transition state of Kd = 10-15 M (1 femtomolar). This is as tight as one of the highest affinity binding interactions in the biological world, the binding of avidin and biotin. As we noted in Chapter 5.1, assuming that the second order rate constant for avidin/biotin binding and as shown above for E/S† is diffusion controlled (about 108 M-1s-1), the off rate for the avidin-biotin or ES† complex is 10-7 s-1, equivalent to a half life of the complex of 80 days. It doesn't get much tighter than that.
Figure \(\PageIndex{20}\) represent an image of an enzyme and three different molecules, 1–3, that could bind to it. Using the analysis above, which molecule do you think represents substrate? Transition state? Product?

Physical Strategies for Rate Enhancement
Intramolecular Catalysis
Consider the hydrolysis of phenylacetate. This reaction, a nucleophilic substitution reaction, could be catalyzed by the addition of the general base acetate to the solution, as described above. Since this reaction rate would double with the doubling of the solution acetate, the reaction is bimolecular (first order in reactant and catalyst). Now consider the same reaction only when the the general base part of the catalyst, the carboxyl group, is part of the reactant phenylacetate. Such a case occurs in the acetylated form of salicylic acid—i.e., aspirin. When the carboxy group is ortho compared to the acetylated phenolic OH, it is in perfect position to accept a proton from water, decreasing the charge development on the O in the transition state. The general base does not have to diffuse to the appropriate site when it is intramolecular with respect to the carbonyl C of the ester link. The rate of this intramolecular base catalysis is about 100 fold greater than of an intermolecular base catalyst like acetate. It is as if the effective concentration of the intramolecular carboxyl base catalyst is much higher due to its proximity to the reaction site.
Another type of reactions involving a carboxyl group (in addition to simple proton transfer) is when the negatively charged carboxyl O acts as a nucleophile and attacks an electrophilic carbonyl carbon. When the carbonyl is part of an ester, the carboxyl group engages in a nucleophilic substitution reaction, expelling the alcohol part of the ester as a leaving group. The remaining examples below consider the nucleophilic (carboxyl) substitution on phenylesters, with phenolate as the leaving group. The reactions in effect transfer an acyl group to the carboxyl group to create an anhydride.
First consider acyl transfer with aspirin derivatives. Aspirin, as you know, contains a carboxyl group ortho to an ester substituent. Hence the carboxyl group can act as a nucleophile and attack the carbonyl carbon of the ester in a nucleophilic substitution reaction. The net effect is to transfer the acetyl group from the phenolic OH to the carboxyl group converting it to an anhydride. This is an intramolecular reaction. Compare this reaction to a a comparable bimolecular reaction shown in Figure \(\PageIndex{21}\).
The first order rate constant of the intramolecular transfer of the acetyl group to the carboxyl group, k1 = 0.02 s-1. The analogous bimolecular reaction rate constant k2~ 10-10 M-1s-1. Dividing k1/k2 gives the relative rate enhancement of the intramolecular over the intermolecular reaction. With units of molarity, this ratio can be interpreted as the relative effective concentration of the intramolecular nucleophile. This makes the effective concentration of the carboxylate in the aspirin derivative 2 x 107 M.
Now consider the cleavage of phenylacetate using acetate as the nucleophile as shown in Figure \(\PageIndex{22}\). The products are acetic anhydride and phenolate. This is a bimolecular reaction (a slow one at that), with a bimolecular rate constant, k2 which I will arbitrarily set to 1 for comparison to some similar reactions.
Now consider a monoester derivatives of succinic acid - phenyl succinate - in which the free carboxyl group of the ester attacks the carbonyl carbon of the ester derivative, as shown in Figure \(\PageIndex{23}\).
If you assign a second order rate constant k2 = 1 M-1s-1 to the analogous intermolecular reaction of acetate with phenylacetate (as described above), the first order rate constant for the intramolecular reaction of phenylsuccinate is 105 s-1. The ratio of rate constants, k1/k2 = 105 M. That is it would take 105 M concentration of acetate reacting with 1 M phenylacetate in the first bimolecular reaction to get a reaction as fast as the intramolecular reaction of phenylsuccinate. The intramolecular reaction of an even more sterically restricted bicyclic phenylcarboxylate shown in Figure \(\PageIndex{24}\) has a k1/k2 = 108 M.
Another example is anhydride formation between two carboxyl groups. The ΔGo for such a reaction is positive, suggesting an unfavorable reaction. Consider two acetic acid molecules condensing to form acetic anhydride. For this intermolecular reaction, Keq = 3x10-12 M-1. Now consider the analogous intramolecular reaction of the dicarboxylic acid succinic acid. It condenses in an intramolecular reaction to form succinic anhydride with a Keq = 8x10-7 (no units). The ratio Keq-intra/Keq inter = 3 x105 M. It is as if the effective concentration of the reacting groups because they do not have to diffuse together to react, is 3 x105 M.
How does this apply to enzyme catalyzed reaction? Enzymes bind substrates in physical steps which are typically fast. The slow step is often the chemical conversion of the bound substrate, which is effectively intramolecular if the initial binding reaction is fast. These three kinds of reactions, intermolecular, intramolecular, and enzyme-catalyzed can be broken down into two hypothetical steps, a binding followed by catalysis as shown in Figure \(\PageIndex{25}\).
If the rate constants for the chemical steps are all identical, the advantage of the intramolecular and enzyme-catalyzed reaction over the intermolecular reaction is KINTRA/KINTER and KENZ/KINTER, respectively.
The advantage of intramolecular reactions can be seen by studying the Ca-EDTA complex. Calcium in solution exists as a octahedrally coordinated complex with water occupying all the coordination sites. EDTA, a multidentate ligand, first interacts through one of its potential six electron donors to Ca in a reaction which is entropically disfavored from the the Ca-EDTA perspective, although one water is released. Once this first intramolecular complex is formed, the rest of the ligands on the EDTA rapidly coordinate with the Ca and release bound water as illustrate in Figure \(\PageIndex{26}\). The former is no longer entropically disfavored since it is now an intramolecular process while the later is favored through the release of the remaining five water molecules.
Figure \(\PageIndex{26}\): Binding of Ca2+ and EDTA
We've shown above the catalytic advantage offered by intramolecular reaction in terms of a dramatic increase in the effective concentration of reactants, which sometimes reached levels of 108 M. Another way is to look at entropy changes associated with dimer formation. The table below shows that an intramolecular reaction is favored over an intermolecular reaction since in the latter, significant decreases in translational and rotation entropy result.
| System | A | B | A-B | ΔS |
|---|---|---|---|---|
| Gas | ||||
| S trans | 30 | 30 | 30 | -30 |
| S rot | 20 | 20 | 20 | -20 |
| S int | 5 | 5 | 20 | +10 |
| Gas → Solution | -10 | -10 | -15 | |
| S sol | 45 | 46 | 55 | -35 (Correspond to 108-109 M) |
Strain Distortion
In organic chemistry, you learned that certain structures such as three-membered and four-membered ring structures, such as epoxides were highly reactive due to the strain distortion inherent to the unfavored bond angles inherent to the ring. Enzyme active sites can also utilize strain distortion within a bound substrate to increase the reactivity of the molecule and favor the formation of the transition state. Many enzymes that function by the induced fit model also utilize strain distortion within their catalytic mechanism. Within the unbound state they remain in a low catalytic state, however the interaction with the substrate induces the destabilization of the enzyme active site or may induce strain within the substrate causing the initiation of the catalytic activity of the enzyme.
A Note on Asymmetric Catalysis/Organocatalysis
In a subsequent section, we will discuss how protein enzymes use the catalytic strategies described above. An intriguing question arises: how much of the structure of a large protein is really needed for catalysis? Much work has been directed to the development of small molecule catalysis mimetics of large protein enzymes. Just how small can you go in reducing the size of a protein and still get catalysis?
One important feature of enzyme catalysis is that they catalyze reactions in which only one enantiomer is produced. That is, the synthesis is asymmetric. This is typically a consequence of the asymmetric enzyme (itself chiral) binding only one enantiomer as a reactant and/or the imposition of steric restrictions on the possible reactions of the bound substrate. L-Pro alone can act as such an asymmetric catalyst in an aldol condensation reaction. Figure \(\PageIndex{27}\):
Catalysts are vital in biological settings but also in the laboratory synthesis of molecules that sustain our culture and economy. Transition metal and, increasingly, protein enzymes have been used as industrial catalysts. They have now been joined by new asymmetric catalysts (a subset of organocatalysts). The work of Benjamin List and David MacMillan, who were instrumental in developing the ideas of asymmetric catalyst, has been recognized by the Nobel Commission which awarded the 2021 Nobel Prize in Chemistry to them.
The enzyme triose phosphate isomerase catalyzes an asymmetric reaction, in which only one enantiomer of glyceraldehyde-3-phosphate is produced from the achiral dihydroxyacetone phosphate. Figure \(\PageIndex{28}\) shows this enantiospecific reaction.
Figure \(\PageIndex{28}\): Reaction catalyzed by triose phosphate isomerase
Figure \(\PageIndex{29}\)s contains an interactive iCn3D model of a triose phosphate isomerase from Trypanosoma brucei brucei (1KV5), which shows a conserved active site Pro 168 (spacefill) and amino acid side chains within 4 Å (stick) within the context of one monomer (cartoon) of the dimeric protein.
AsymCat.png?revision=1&size=bestfit&width=266&height=212)
References
Amyes TL, Richard JP. Biochemistry. 2013, 52(12), 2021-35. doi: 10.1021/bi301491r
Ferst and Kirby, J. Am. Chem. Soc. 1967, 89, 19, 4857–4863. https://doi-org.ezproxy.csbsju.edu/10.1021/ja00995a007
Komiyama et al., PNAS, 1977, 74 (7) 2634-2638. https://doi.org/10.1073/pnas.74.7.263
Lerner, R. A., & Tramontano, A. (1987). Antibodies as enzymes. Trends in Biochemical Sciences, 12, 427-430. https://doi.org/10.1016/0968-0004(87)90208-8
OpenStax College. (2022). Chemistry. OpenStax. https://openstax.org/details/books/chemistry-2e
Regan, C. K., Craig, S. L., & Brauman, J. I. Science. 2002 295(5563), 2245-2247. DOI: 10.1126/science.1068849



