4: Dilution Worksheet and Problems
- Page ID
- 3254
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
- Understand how to quantify bacterial cells.
- Learn how to solve a dilution problem.
It is a common practice to determine microbial counts for both liquid and solid specimens--suspensions of E. coli in nutrient broth all the way to soil samples and hamburger meat. Most specimens have high enough numbers of microorganisms that the specimen has to be serially diluted to quantitate effectively. The following is a step-by-step procedure to working dilution problems, and includes some practice problems at the end.
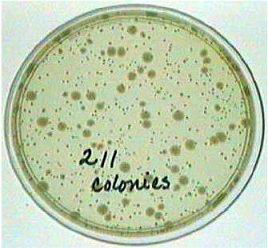
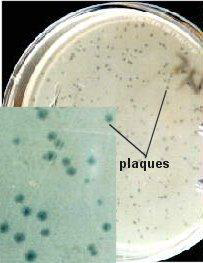
The purpose can be determination of bacterial, fungal, or viral counts (indirectly). This protocol is specific for bacterial counts (colony-forming units, CFUs), but can be modified for fungi (CFUs) and viruses (plaque-forming units, PFUs for viral counts). A set of serial dilutions is made, a sample of each is placed into a liquefied agar medium, and the medium poured into a petri dish. The agar solidifies, with the bacterial cells locked inside of the agar. Colonies grow within the agar, as well as on top of the agar and below the agar (between the agar and the lower dish). The procedure described above produces a set of pour plates from many dilutions, but spread plates (sample spread on top of solidified agar) can be used also. The agar plate allows accurate counting of the microorganisms, resulting from the equal distribution across the agar plate. This cannot be done with a fluid solution since 1) one cannot identify purity of the specimen, and 2) there is no way to enumerate the cells in a liquid.
SOLVING DILUTION PROBLEMS
Note
colony count on agar plate
THE STANDARD FORMULA = ___________________________________________________________
total dilution of tube (used to make plate for colony count) X amount plated
To work the problem, you need 3 values---a colony count from the pour or spread plates, a dilution factor for the dilution tube from which the countable agar plate comes, and the amount of the dilution that was plated on the agar plate.
STEP 1:Determine the appropriate plate for counting
Look at all plates and find the one with 30-300 colonies (or plaques), preferably. Greater than 300 and less than 30 is a high degree of error. Air contaminants can contribute significantly to a really low count and a high count can be confounded by error in counting too many small colonies. Use the total dilution for the tube from where the plate count was obtained. If duplicate plates (with same amount plated) have been made from one dilution, average the counts together.
STEP 2:Determine the total dilution for the dilution tubes
Dilution = amount of specimen transferred divided by the [amount of specimen transferred + amount already in tube].
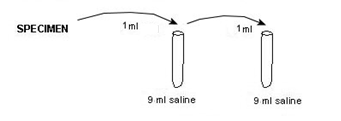
Determine the dilution factor for each tube in the dilution series. Multiply the individual dilution of the tube X previous total dilution. To calculate this dilution series:
Note
amount of sample
Dilution factor for each tube in a set = _______________________________________
amount of sample + amount of diluent in tube
But after the first tube, each tube is a dilution of the previous dilution tube.
Note
Total dilution factor = previous dilution of tube X dilution of next container
Example: FOR THE ABOVE DILUTION SERIES
1 ml added to 9ml = 1/10 for 1st tube
1ml added to 9ml = 1/10 for 2nd tube
previous dilution of 1/10 (1st tube) X 1/10 (2nd tube) = total dilution of 1/100 (=10-2=1/102)
STEP 3: Determine the amount plated
The amount plated is the amount of dilution used to make the particular pour plate or spread plate.
There is nothing to calculate here: the value will be stated in the procedure, or it will be given in the problem.
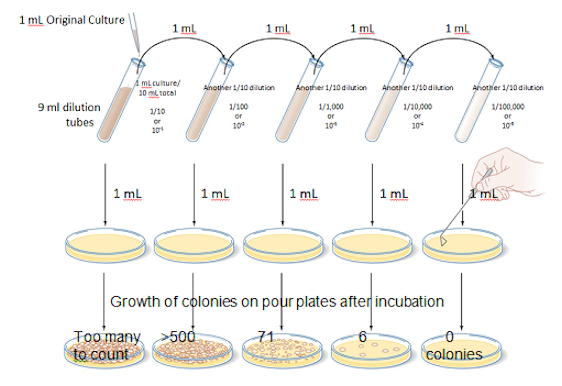
Solving the above problem
- The countable plate is the one with 71 colonies.
- The total dilution of 3rd tube from which above pour plate was made = 1/10 X 1/10 X 1/10 = 1/103
- The amount used to make that pour plate = 1ml
71 colonies
__________ = 71 X 103 = 7.1 X 104 (scientific notation) OR 71,000/ml
1/103 X 1
Note: Rules for Scientific Notation
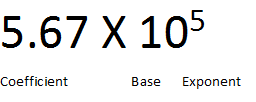
For a number to be in correct scientific notation, the following conditions must be true:
- The coefficient must be greater than or equal to 1 and less than 10.
- The base must be 10.
- The exponent must show the number of decimal places that the decimal needs to be moved to change the number to standard notation. A negative exponent means that the decimal is moved to the left when changing to standard notation.
Questions
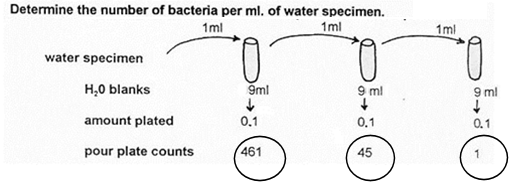
1. Determine the number of bacteria per ml. of water specimen.
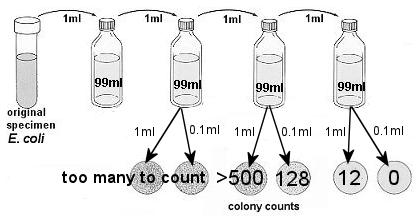
2. Determine the number of bacterial cells per ml. in the original culture.
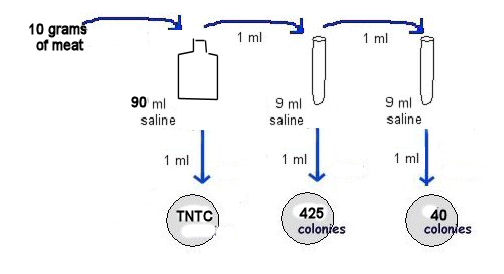
3. Determine the number of bacterial cells per gram of meat.
Contributors
Jackie Reynolds, Professor of Biology (Richland College)

