1.3: Physical-Chemical Foundations

Search Fundamentals of Biochemistry

Learning Goals (ChatGPT o3-mini)

1. Understand the Driving Forces of Reactions

   • Explain how energy differences (ΔG) between reactants and products dictate the spontaneity and extent of chemical reactions.
   • Use the “ball on a hill” analogy to relate potential energy differences to reaction spontaneity.

2. Distinguish Reversible and Irreversible Reactions

   • Describe the characteristics of irreversible reactions versus reversible reactions and illustrate how reaction progress and equilibrium are reflected in concentration-time profiles.
   • Interpret different scenarios (favoring products, favoring reactants, or balanced) based on changes in reactant and product concentrations.

3. Apply Equilibrium Concepts

   • Define the equilibrium constant (Kₑ_q) and explain how it quantitatively reflects the relative favorability of reactants versus products.
   • Relate the value of Kₑ_q (greater than, less than, or equal to 1) to the extent of reaction and spontaneous direction.

4. Analyze the Role of Concentration in Reaction Energetics

   • Differentiate between the intrinsic stability of reactants/products (ΔG⁰) and the influence of concentration on reaction spontaneity via the reaction quotient (Q_rx).
   • Explain how changing concentrations (as per Le Chatelier’s Principle) can shift equilibrium positions.

5. Calculate and Interpret Gibbs Free Energy Changes

   • Use the relationship ΔG = ΔG⁰ + RT ln Q to calculate the free energy change under non-standard conditions.
   • Discuss how the sign and magnitude of ΔG determine whether a reaction proceeds toward products, remains at equilibrium, or reverses.

6. Connect Thermodynamic Parameters: Enthalpy and Entropy

   • Define enthalpy (ΔH) and entropy (ΔS) and explain their roles in determining the spontaneity of both exothermic and endothermic reactions.
   • Compare and contrast exothermic (ΔH < 0) and endothermic (ΔH > 0) processes in the context of biological reactions.

7. Integrate the Second Law of Thermodynamics in Biochemical Contexts

   • Explain the significance of the second law of thermodynamics (ΔS_total > 0) and how it governs spontaneous processes.
   • Relate macroscopic thermodynamic changes (ΔG_sys) to microscopic rearrangements and energy dispersion (ΔS_sys and ΔS_surr) in biochemical systems.

8. Apply Thermodynamic Principles to Real-World Biochemical Reactions

   • Analyze case studies, such as the reactions of strong versus weak acids with water, to illustrate how intrinsic molecular stability and concentration effects combine to determine reaction direction and extent.
   • Evaluate the thermodynamic rationale behind phenomena like water evaporation and molecular binding, and discuss how these principles underpin cellular metabolism.

By achieving these learning goals, students will be equipped to analyze and predict the behavior of biochemical reactions, understand the interplay between energy, equilibrium, and entropy, and apply these concepts to complex biological systems.

The types and numbers of chemical reactions in biological cells are staggering. Compared to physical and chemical reactions in a controlled and closed environment, biological reactions occur in open systems with input and output of energy and chemical "feedstocks." Yet, they are governed by the same physical principles that control all reactions. We can gain insight into biological reactions and how they are controlled by considering the principles you have used in many preceding classes: energy changes, equilibria, and thermodynamics. Let's review them!

Reactions and Energy Changes

Why do reactions vary in extent from completely irreversible in the forward reaction to reversible reactions favoring the reactants? It might help to understand a simple physical reaction before we try more complicated chemical reactions. Let's start with a simple ball on a hill. Does a ball at the top of a hill roll downhill spontaneously, or does the opposite happen? No one has ever seen a ball roll spontaneously uphill unless a lot of energy was added to the ball. This physical reaction appears irreversible and occurs because the ball has lower potential energy at the bottom of the hill than it does at the top. The gap in the potential energy is related to the "extent" and spontaneity of this reaction. As we have undoubtedly observed, natural processes tend to go to a lower energy state. By analogy, we will consider the driving force for a chemical reaction to be the free energy difference, ΔG, between reactants and products. ΔG determines the extent and spontaneity of the reaction.

Reversible/Irreversible Reactions, Extent of Reactions, Equilibria

Consider a hypothetical reversible reaction in which you start with some reactants, \(\ce{A}\) and \(\ce{B}\), each at a 1 M concentration (1 mol of each/L solution). but no products, \(\ce{P}\) and \(\ce{Q}\). For ease, assume that the total volume of solution is 1 L, so that we start with 1 mol each of \(\ce{A}\) and \(\ce{B}\). At time \(t=0\), the concentration of products is 0. The reaction can be written as:

\[\ce{A + B <=> P + Q}. \nonumber \]

As time progresses, the amounts or concentrations of \(\ce{A}\) and \(\ce{B}\) decrease as the amounts or concentrations of products \(\ce{P}\) and \(\ce{Q}\) increase. At some time, no further changes occur in the amount or concentrations of remaining reactants or products. At this point, the reaction is in equilibrium, a term often used in our common vocabulary to denote a system undergoing no net change.

Most of the reactions we will study occur in solution, so we will deal with concentrations (mol/L or mmol/mL = M). Let's consider how the concentration of reactants and products changes as a function of time. Depending on the extent to which a reaction is reversible, four different scenarios can be imagined:

Scenario 1: Irreversible reaction in which the reverse reaction occurs to a negligible extent.

In this reaction, the reverse reaction occurs to such a small extent that we can neglect it. The only reaction that occurs is the conversion of reactants to products. Hence, all the reactants are converted to product. At equilibrium [A] = 0. Since 1 mol of A reacted, it must form 1 mol of P and 1 mol Q - i.e., the concentration of products at equilibrium is 1 M. At an earlier time of the reaction (let's pick a time when [A] = 0.8 M), only part of the reactants have reacted (in this case 0.2 M), producing an equal amount of products, P and Q. Graphs of [A] and [P] as a function of time are shown below. [A] decreases nonlinearly to 0 M while [P] increases reciprocally to 1 M concentration. This is illustrated in the graph below.

Examples of irreversible reactions are reactions of strong acids (nitric, sulfuric, hydrochloric) with bases (OH^- and water) or the much more complicated combustion reactions, such as the burning of sugars (like trees) and hydrocarbons (like octane) to form CO₂ and H₂O.

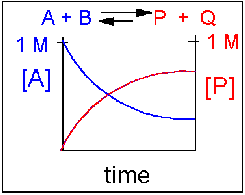
Scenario 2: Reversible reaction in which the forward reaction is favored.

Again, [A] decreases and [P] increases, but in this case, some A remains since the reaction is reversible. As [A ]and [B] decrease, [P] and [Q] increase, which increases the chance that they will collide and form the product. Since P and Q can react to form reactants, the [A] at equilibrium is not zero, as is shown below.

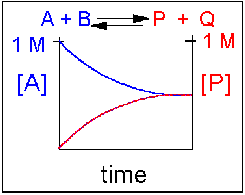
Scenario 3: Reversible Reaction in which forward and reverse reactions are equally favored.

Again, [A] decreases and [P] increases, but in this case, some A remains since the reaction is reversible. As [A] and [B] decrease, [P] and [Q] increase, which increases the chance that they will collide and form the product. Since P and Q can react to form reactants, the [A] at equilibrium is not zero, as is shown below. Because the reactants and products are equally favored, their concentrations will be equal at equilibrium.

Scenario 4: Reversible Reaction in which the reverse reaction is favored.

Again, [A] decreases, and [P] increases, but in this case, some A remains since the reaction is reversible. As [A] and [B] decrease, [P] and [Q] increase, which increases the chance that they will collide and form the product. Since P and Q can react to form reactants, the [A] at equilibrium is not zero, as shown below. Because the reaction favors reactants, their concentration will be higher at equilibrium than the products.

An example of this kind of reaction, one that favors reactants, is the reaction of acetic acid (a weak acid) with water.

\[\ce{CH3CO2H(aq) + H2O(l) <=> H3O^{+}(aq) + CH3CO2^{-}(aq)} \nonumber \]

Equilibrium Constants

Without much experience in chemistry, it is difficult to just look at the reactants and products and determine whether the reaction is irreversible or reversible, favoring either reactants or products (except obvious irreversible reactions described above). However, this data can be found in tables of equilibrium constants. The equilibrium constant, as its name implies, is constant, independent of the concentration of the reactants and products. A \(K_{eq} > 1\) implies that the products are favored. A \(K_{eq} < 1\) implies that reactants are favored. Reactants and products are equally favored when \(K_{eq} = 1\). For the more general reaction,

\[\ce{aA + bB <=> pP + qQ} \nonumber \]

where \(a\), \(b\), \(p\), and \(q\) are the stoichiometric coefficients,

\begin{equation}
\mathrm{K}_{\mathrm{eq}}=\frac{[\mathrm{P}]_{\mathrm{eq}}^{\mathrm{p}}[\mathrm{Q}]_{\mathrm{eq}}^{\mathrm{q}}}{[\mathrm{A}]_{\mathrm{eq}}^{\mathrm{a}}[\mathrm{B}]_{\mathrm{eq}}^{\mathrm{b}}}
\end{equation}

where all the concentrations are at their equilibrium values. For a simple reaction where \(a\), \(b\), \(p\), and \(q\) are all 1, then \(K_{eq} = ([P] [Q])/([A] [B]) \).

(Note: Equilibrium constants are truly constant only at a given temperature, pressure, and solvent condition. Likewise, they depend on concentration to the extent that their activities change with concentration.)

For an irreversible reaction, such as the reaction of a 0.1 M HCl (aq) in water, [HCl]_eq = 0, you cannot easily measure a K_eq. However, if we assume the reaction goes in reverse to an almost imperceptible degree, [HCl]_eq might equal 10-10 M. Hence K_eq >> 1.

In summary, the extent of reactions can vary from completely irreversible (favoring only the products) to reactions that favor the reactants.

Our next goal is to understand what controls the extent of a reaction. That is, of course, the change in the Gibbs free energy. Two different pairs of factors influence the ΔG. One pair is the reactants' concentration and inherent reactivity compared to products (as reflected in the Keq). The other pair is enthalpy/entropy changes. We will now consider the first pair.

Contributions of Molecule Stability (K_eq) and Concentration to ΔG

Consider the reactions of hydrochloric acid and acetic acid with water.

\[\begin{align*} \ce{HCl (aq) + H2O (l)} & \ce{-> H3O^{+}(aq) + Cl^{-} (aq)} \\[4pt] \ce{CH3CO2H (aq) + H2O (l) } & \ce{-> H3O^{+} (aq) + CH3CO2^{}- (aq)} \end{align*} \nonumber \]

Assume that at t = 0, each acid is placed into water at a concentration of 0.1 M. When equilibrium is reached, essentially no HCl remains in the solution. In contrast, 99% of the acetic acid remains. Why are they so different? We rationalized that HCl (aq) is a much stronger acid than H₃O⁺(aq) which itself is a much stronger acid than CH₃CO₂H (aq). Why? Something about the structure of these acids (and the bases) makes HCl much more intrinsically unstable, much higher in energy, and hence much more reactive than the acid it forms, H₃O⁺(aq). Likewise, H₃O⁺(aq) is much more intrinsically unstable, much higher in energy, and hence more reactive than CH₃CO₂H (aq). This has nothing to do with concentration since the initial concentration of both HCl (aq) and CH₃CO₂H (aq) were identical. This observation is reflected in the K_eq for these acids (>>1 for HCl and <<1 for acetic acid). This difference in intrinsic stability of reactants compared to products (which is independent of concentration) is one factor that contributes to ΔG.

The other factor is concentration. A 0.25 M (0.25 mol/L or 0.25 mmol/ml) solution of acetic acid does not conduct electricity, implying that very few ions of H₃O⁺(aq) + CH₃CO₂^- (aq) exist in the solution. However, a dim light becomes evident if more concentrated acetic acid is added. Adding more reactants seemed to drive the reaction to form more products, even though the reverse reaction is favored if one considers only the intrinsic stability of reactants and products. Before the concentrated acid was added, the system was at equilibrium. Adding concentrated acid perturbed the equilibrium, which drove the reaction to form additional products. This is an example of Le Chatelier's Principle, which states that if a reaction at equilibrium is perturbed, the reaction will be driven in the direction that will relieve the perturbation. Hence:

• if more reactant is added, the reaction shifts to form more products
• if more product is added, the reaction shifts to form more reactants
• if products are selectively removed (by distillation, crystallization, or further reaction to produce another species), the reaction shifts to form more product.
• if reactants are removed (as above), the reaction shifts to form more reactants.
• if heat is added to an exothermic reaction, the reaction shifts to remove the excess heat by shifting to form more reactants. (opposite for an endothermic reaction).

Change in Free Energy G

Without doing a complicated derivation, these simple examples suggest that the total \(ΔG\) can be expressed as the sum of the two contributions showing the effects of the intrinsic stability (\(K_{eq}\)) and concentration:

\begin{equation}
\Delta G_{\text {total }}=\Delta \mathrm{G}_{\text {stability }}+\Delta \mathrm{G}_{\text {concentration }}
\end{equation}

which becomes for the simple reaction \(\ce{A + B <=> P + Q}\) (after a rigorous derivation):

\begin{equation}
\begin{aligned}
\Delta G &=\Delta G^0+R T \ln \frac{[\mathrm{P}][\mathrm{Q}]}{[\mathrm{A}][\mathrm{B}]} \\
&=\Delta G^0+R T \ln \mathrm{Q}_{\mathrm{rx}}
\end{aligned}
\end{equation}

where ΔG^o reflects the contribution from the relative intrinsic stability of reactants and products, and the second term reflects the contribution from the relative concentrations of reactants and products (which has nothing to do with stability). Q_rx is the reaction quotient, which for the reaction A + B ↔ P + Q is given by:

\begin{equation}
Q_{r x}=([P][Q]) /([A][B])
\end{equation}

at any point in the reaction.

Meaning of ΔG

Remember that ΔG is the "driving" force for a reaction, analogous to the difference in potential energy for a ball on a hill. Go back to that analogy. If the ball starts at the top of the hill, does it roll downhill? Of course. It goes from high potential energy to low potential energy. The reaction can be written as:

Ball _top → Ball _bottom

for which the change in potential energy, ΔPE = PE_bottom -PE_top< 0. If the ball starts at the bottom, will it go to the top? Obviously not. For that reaction,

Ball _bottom → Ball _top, ΔPE > 0.

If the top of the hill were at the same height as the bottom of the hill (obviously an absurd situation), the ball would not move. It would effectively be at equilibrium, a state of no change. For this reaction, Ball _top --> Ball _bottom, the ΔPE = 0. As the ball starts rolling down the hill, its potential energy gets closer to the potential it would have at the bottom. Hence, the ΔPE changes from negative to more and more positive until it gets to the bottom, at which case the ΔPE = 0, and movement ceases. If the ΔPE is not 0, the ball will move until the ΔPE = 0.

Likewise, for a chemical reaction that favors products, ΔG < 0. The system is not at equilibrium, and the reaction will go toward products. As the reaction proceeds, products build up, and there is less of a driving force for reactants to go to products (Le Chatelier'sPrinciple), so the ΔG becomes more positive until the ΔG = 0 and the reaction is at equilibrium. A reaction with a ΔG > 0 is likewise not at equilibrium, so it will go in the appropriate direction until equilibrium is reached. Hence, for the reaction A + B <==> P + Q,

• if ΔG < 0, the reaction goes toward products P and Q
• if ΔG = 0, the reaction is at equilibrium, and no further change occurs in the concentration of reactants and products.
• if ΔG > 0, the reaction goes toward reactants A and B.

We can not measure easily the actual free energy G of reactants or products, but we can measure ΔG readily. These points are illustrated in the graph below of ΔG vs time for the hypothetical reaction A + B ↔ P + Q. (Also notice the two insert graphs - in blue and red - which show, in analogy to the ball on the hill graphs, the values of ΔG at the two points where the perturbation to the equilibrium was made.)

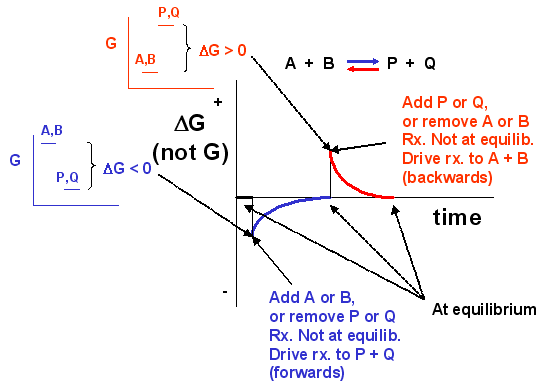
Notice the ΔG is constantly changing until the system reaches equilibrium. Initially, the equilibrium is perturbed so that the system is not in equilibrium (shown in blue). The perturbation was such that the products were favored. After reaching equilibrium, the system was perturbed again to favor the reverse reaction. Notice, in this case, the ΔG for the reaction as written: A + B ↔ P + Q is positive - i.e., it is not in equilibrium. Therefore, the reaction (as written) goes backward to reactants. It is important to realize that the reported ΔG is for the reaction as written.

Now let's apply ΔG = ΔG^o + RTln Q = ΔG^o + RTln ([P][Q])/([A][B]) to two reactions we discussed above:

• HCl(aq) + H₂O(l) ↔ H₃O⁺(aq) + Cl^-(aq)
• CH₃CO₂H(aq) + H₂O(l) ↔ H₃O⁺(aq) + CH₃CO₂^-(aq)

At time t=0, 0.1 mole of HCl and CH₃CO₂H were added to two different beakers. The forward reaction is favored at this point, but obviously to different extents. The RTln Q would be identical for both acids since each reactant is at 0.1 M, but no products exist. However, the ΔG^o is negative for HCl and positive for acetic acid since HCl is a strong acid. Hence at t=0, ΔG for the HCl reaction is much more negative than for acetic acid. This is summarized in the table below. The direction of the arrow shows if products (-->) or reactants (<---) are favored. The size of the arrow shows very approximately to what extent the ΔG term is favored

Reaction at t=0	ΔG^o	RTln Q	ΔG
HCl(aq) + H2O(l)	--------------->	--------------->	----------------------------->
CH3CO2H(aq) + H2O(l)	<-------------	--------------->	->

Now, when equilibrium is reached, no net change occurs in the concentration of reactants and products, and ΔG = 0. In the case of HCl, there is just an infinitesimal amount of HCl left and 0.1 M of each product, so concentration favors HCl formation. However, the intrinsic relative stability of reactants and products still favors products. In the case of acetic acid, most acetic acid remains (0.099 M) with little product (0.001 M), so concentration favors products. However, the intrinsic relative stability of reactants and products still favors reactants. This is summarized in the table below.

Reaction at equlib.	ΔG^ostab	RTln Q	ΔG
HCl(aq) + H2O(l)	--------------->	<---------------	favors neither, = 0
CH3CO2H(aq) + H2O(l)	<-------------	-------------->	favors neither, = 0

Compare the two tables above (one at time t= 0 and the other at equilibrium). Notice:

• ΔG^o does not change in a given set of conditions since it has nothing to do with concentration.
• Only RTln Q changes during a reaction until equilibrium is achieved.

Meaning of ΔG^o

To get a better meaning of the significance of ΔG^o, let's consider the following equations under two different conditions:

\begin{equation}
\Delta G=\Delta G^0+R T \ln \frac{[\mathrm{P}][\mathrm{Q}]}{[\mathrm{A}][\mathrm{B}]}=\Delta G^0+R T \ln \mathrm{Q}_{\mathrm{rx}}
\end{equation}

Condition I: Reaction at equilibrium, ΔG = 0

The equation reduces to:

\begin{equation}
\Delta G^0=-R T \ln \frac{[\mathrm{P}]_{\mathrm{eq}}[\mathrm{Q}]_{\mathrm{eq}}}{[\mathrm{A}]_{\mathrm{eq}}[\mathrm{B}]_{\mathrm{eq}}}=-2.303 \mathrm{R} T \log \mathrm{K}_{\mathrm{eq}}
\end{equation}

This supports our idea that ΔG^o is independent of concentration since K_eq should also be independent of concentration.

Condition II: The concentration of all reactants and products is 1 M (standard state, assuming solution reaction)

The equation reduces to:

\begin{equation}
\begin{aligned}
\Delta G=\Delta G^0+R T \ln \frac{[1][1]}{[1][1]}=\Delta G^0+2.303 R T \log 1=\Delta G^0 \\
\Delta G &=\Delta G^o+R T \ln \left(\frac{[1][1]}{[1][1]}\right) \\
&=\Delta G^o+2.303 R T \log 1 \\
&=\Delta G^o
\end{aligned}
\end{equation}

This implies that when all reactants are at this concentration, defined as the standard state (1 M for solutes), the ΔG at that particular moment is the ΔG^o for the reaction. If one of the reactants or products is H₃O⁺, it would make little biological sense to calculate ΔG^o for the reaction using the standard state of [H₃O⁺] = 1 M or a pH of zero. Instead, it is assumed that the pH = 7, [H₃O⁺] = 10^-7 M. A new symbol is used for ΔG^o under these conditions, ΔG^o'.

Heat, Enthalpy and Entropy

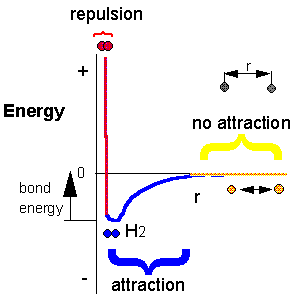
Consider the association reaction of hydrogen atoms into molecular hydrogen

\[\ce{H + H -> H2}. \nonumber \]

Does this reaction occur spontaneously? It does. You should remember that individual \(\ce{H}\) atoms are unstable since they don't have a completed outer shell of electrons - in this case, a duet. As they approach, they can interact to form a covalent bond and, in the process, release energy. The bonded state is a lower energy state than two separated H atoms. This should be clear since energy has to be added to a molecule of \(\ce{H2}\) to break the bond. We call this the bond dissociation energy.

`

Now consider a more complicated reaction, the burning of octane.

\[\ce{2C8H18(l) + 25O2(g) → 16CO2(g) + 18H2O(g)} \nonumber \]

To carry out this reaction, every C-C, C-H, and O-O bond in the reactants must be broken (which requires an input of energy), but lots of energy is released when the products' C-O and H-O covalent bonds are formed. Is more energy needed to break the bonds in the reactants, or is more energy released when forming bonds in the product? The answer should be clear. The products must be at a lower energy than the reactants since large amounts of heat and light energy are released from combustion of gasoline and other hydrocarbons.

These reactions suggest that energy must be released for a reaction to proceed to any extent in a given direction.

Now consider, however, the following reaction:

\[\ce{Ba(OH)2. 8H2O(s) + 2NH4SCN(s) -> 10H2O(l) + 2NH3(g) + Ba(SCN)2(aq)} \nonumber \]

When these two solids are added to a beaker and stirred, a reaction occurs, as evidenced by the formation of a liquid (water) and the smell of ammonia. Surprisingly, heat is not released into the surroundings in this reaction. Instead, heat was absorbed from the surroundings, turning the beaker so cold that it froze to a piece of wood (with a layer of water added to the wood) on which it was placed. This reaction seems to violate our idea that a reaction proceeds in a direction in which heat is liberated. Reactions that liberate heat and raise the temperature of the surroundings are called exothermic reactions. Reactions that absorb heat from the surroundings and, hence, lower the temperature of the surroundings are endothermic reactions. To answer the question, we need to consider entropy.

A review of thermodynamics

You may remember from General Chemistry that the change in the internal energy of a system, \(ΔE\), is given by:

\begin{equation}
\begin{aligned}
\Delta E_{s y s} &=q+w \\
&=q-P_{e x t} \Delta V
\end{aligned}
\end{equation}

where \(q\) is the heat (thermal energy) transferred to (+) or from the system (-), \(w\) is the work done on (+) or by (-) the system. This is one expression for the 1^st Law of Thermodynamics

If only pressure/volume (PV) work is done (and not electrical work, for example), \(w = - P_{ext}ΔV\), where \(P_{ext}\) is the external pressure resisting a volume change in the system, \(ΔV\). Under these conditions, the heat transfer at constant \(P\), \(q_P\) is given by:

\begin{equation}
\begin{aligned}
\Delta \mathrm{E}_{\mathrm{sys}}-\mathrm{w} &=\Delta \mathrm{E}_{\mathrm{sys}}+\mathrm{P}_{\mathrm{ext}} \Delta \mathrm{V} \\
&=\mathrm{q}_{\mathrm{P}} \\
&=\Delta \mathrm{H}_{\mathrm{sys}}
\end{aligned}
\end{equation}

\(q_p\), which can easily be measured in a coffee cup calorimeter, is equal to the change in enthalpy, \(ΔH\), of the system.

For exothermic reactions, the reactants have more thermal energy than the products, and the heat energy (measured in kilocalories or kilojoules) released is the difference between the energy of the products and reactants. When heat energy is used to measure the difference in energy, we call the energy enthalpy (\(H\)) and the heat released as the change in enthalpy (\(ΔH\)), as illustrated below.

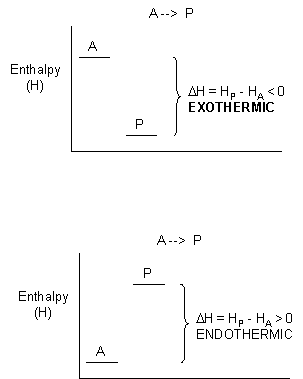
For exothermic reactions, \(ΔH < 0\). For endothermic reactions, \(ΔH > 0\).

The equation \(\Delta \mathrm{E}_{\mathrm{sys}}=\mathrm{q}+\mathrm{w}=\mathrm{q}-\mathrm{P}_{\mathrm{ext}} \Delta \mathrm{V}\) is one expression of the First Law of Thermodynamics. Another statement of energy conservation is:

\begin{equation}
\Delta \mathrm{E}_{\text {tot }}=\Delta \mathrm{E}_{\text {universe }}=\Delta \mathrm{E}_{\text {sys }}+\Delta \mathrm{E}_{\text {surrounding }}=0
\end{equation}

Something other than heat being released from the system decides whether a reaction proceeds to a significant extent. That is, the spontaneity of a reaction must depend on more than just ΔH_sys. Another example of a spontaneous natural reaction is the evaporation of water (a physical, not chemical, process).

\[\ce{H2O (l) → H2O (g)} \nonumber \]

Heat is absorbed from the surroundings to break the intermolecular forces (H bonds) among the water molecules (the system), turning the liquid into a gas. If the surroundings are the skin, evaporating water in the form of sweat cools the body. Why are these reactions spontaneous and essentially irreversible even though they are endothermic? Notice that in both of these endothermic reactions (the reactions of Ba(OH)₂.8H₂O(s) and 2NH₄SCN(s) and the evaporation of water), the products are more disorganized (more disordered) than the products. A solid is more ordered than a liquid or gas, and a liquid is more ordered than a gas. In nature, ordered things become more disordered with time. Entropy (S), the other factor (in addition to enthalpy changes), is often considered to measure a system's disorder. The greater the entropy, the greater the disorder. For reactions that go from order (low S) to disorder (high S), the change in S, ΔS > 0. For the reaction that proceeds from low order to high order, ΔS < 0.

Caution

However, this common description of entropy is quite misleading. Macroscopic examples describing order/disordered states (such as the cleanliness of your room or the shuffling of a deck of cards) are inappropriate since entropy deals with microscopic states.

The driving force for spontaneous reactions is the dispersion of energy and matter. Increases in entropy for reactions that involve matter occur when gases or solutes in solution are dispersed, leading to increases in positional entropy. For reactions involving energy changes, entropy increases when energy is dispersed as random, undirected thermal motion, leading to increases in thermal entropy. In this sense, entropy, \(S\) (a measure of ("spreadedness") is a measure of the number of different ways (microstates) that particles or energy can be arranged (W), not a measure of disorder! W is an abbreviation for the German word,  Wahrscheinlichkeit, which means probability. It can be shown that for a solute dissolving in a solvent, W_sys = W_solute x W_solvent. Note that this is a multiplicative function. Entropy is a logarithmic function of W, which allows additivity of solute and solvent W values, a feature found in other thermodynamic state functions like ΔE, ΔH, and ΔS. Hence

\begin{equation}
\ln W \text { sys }=\ln W_{\text {solute }}+\ln W_{\text {solvent }}
\end{equation}

Boltzmann showed that for molecules,

\begin{equation}
S=k \ln W
\end{equation}

where \(k\) is the Boltzmann constant (1.68 x 10^-23 J/K), S units: J/K

or

\begin{equation}
S=k N_A \ln W=R \ln W
\end{equation}

Boltzmann realized the connection between the macroscopic entropy of a system and the microscopic order/disorder of a system through the equation \(S = k\ln W\). Increasing S (macroscopic property) occurs with increasing numbers of possible microscopic states for the atoms and molecules of a system.

The dissolution of a solute in water and the expansion of a gas into a vacuum, which both proceed spontaneously toward an increase in matter dispersal, are examples of familiar processes characterized by a ΔS_sys > 0. We will see in future chapters that entropy changes in the solvent, solutes, and protein are critical determinants of protein folding.

The spontaneity of exothermic and endothermic processes will depend on the

\begin{equation}
\Delta S_{t o t}=\Delta S_{\text {surr }}+\Delta S_{\text {sys }}
\end{equation}

ΔS_sys often depends on matter dispersal (positional entropy). ΔS_surr depends on energy changes in the surroundings, ΔH_surr = -ΔH_sys (thermal entropy).

It is more convenient to express thermodynamic properties based on the system that is being studied, not on the surroundings. This can be readily done for the ΔS_surr, which depends on ΔH_sys and the temperature. First, consider the dependency on ΔH_sys. Thermal energy flows into or out of the system, and since ΔH_sys = - ΔH_surr,

\(ΔS_{surr}\) is proportional to -ΔH_sys

• For an exothermic reaction, ΔS_surr > 0 (since ΔH_sys < 0) and the reaction is favored;
• For an endothermic reaction, ΔS_surr < 0, (since ΔH_sys > 0), and the reaction is disfavored;

\(ΔS_{surr}\) also depends on the temperature T of the surroundings:

\(ΔS_{surr}\) is proportional to 1/T

If the T_surr is high, a given heat transfer to or from the surroundings will have a smaller effect on the \(ΔS_{surr}\). Conversely, if the T_surr is low, the effect on ΔS_surr will be greater. (Atkins uses the analogy of the effect of a sneeze in a library compared to a crowded street; An American Chemistry General Chemistry text uses the analogy of giving $5 to a friend with $1000 compared to one with just $10.) Hence,

\begin{equation}
\Delta S_{\mathrm{surr}}=\frac{-\Delta \mathrm{H}_{\mathrm{sys}}}{\mathrm{T}}
\end{equation}

(Note: from a more rigorous thermodynamic approach, entropy can be determined from \begin{equation}
\mathrm{dS}=\frac{\mathrm{dq}_{\mathrm{rev}}}{\mathrm{T}}
\end{equation}

Once again,

\begin{equation}
\Delta S_{\text {tot }}=\Delta S_{\text {surr }}+\Delta S_{\text {sys }}
\end{equation}

\(ΔS_{tot}\) depends on both enthalpy changes in the system and entropy changes in the surroundings. Hence,

\begin{equation}
\Delta S_{\text {tot }}=\frac{-\Delta \mathrm{H}_{\mathrm{sys}}}{\mathrm{T}}+\Delta \mathrm{S}_{\mathrm{sys}}
\end{equation}

Multiplying both sides by \(-T\) gives

\begin{equation}
-\mathrm{T} \Delta \mathrm{S}_{\mathrm{tot}}=\Delta \mathrm{H}_{\mathrm{sys}}+\mathrm{T} \Delta \mathrm{S}_{\mathrm{sys}}
\end{equation}

The thermodynamic function Gibb's Free Energy, \(G\), can be defined as:

\begin{equation}
G=H-T S
\end{equation}

At constant \(T\) and \(P\),

\begin{equation}
\Delta G=\Delta H-T \Delta S
\end{equation}

Hence

\begin{equation}
\Delta G_{s y s}=\Delta H_{s y s}-T \Delta S_{s y s}=-T \Delta S_{t o t}
\end{equation}

Spontaneity is determined by \(ΔS_{tot}\) OR \(ΔG_{sys}\) since \(ΔS_{tot} = -ΔG_{sys}/T\). \(ΔG_{sys}\) is widely used in discussing spontaneity since it is a state function, depends only on the enthalpy and entropy changes in the system, and is negative (as is the potential energy change for a falling object) for all spontaneous processes.

The second law of thermodynamics can be succinctly stated: For any spontaneous process, the \(ΔS_{tot} > 0\). Unlike energy (from the First Law), entropy is not conserved.

Summary

Chapter Summary: Reaction Energetics and Thermodynamics in Biological Systems

This chapter delves into the fundamental principles governing the vast array of chemical reactions that occur within biological cells. It begins by framing these reactions in the context of open systems, where both energy and chemical feedstocks flow in and out, yet the underlying behavior is dictated by the same thermodynamic laws that control all chemical processes.

Key Concepts and Analogies

• The chapter introduces the concept of free energy (ΔG) as the driving force of reactions, using the simple "ball on a hill" analogy to illustrate how reactions move from higher to lower energy states.
• It explains how the extent and spontaneity of reactions are determined by the free energy difference between reactants and products, much like a ball rolling downhill due to a drop in potential energy.

Reversible and Irreversible Reactions

• The discussion differentiates between irreversible reactions (where the reverse process is negligible) and reversible reactions, which can reach equilibrium.
• Four scenarios are described, ranging from reactions that go to completion (irreversible) to those where the equilibrium favors either the products, the reactants, or is balanced equally.

Equilibrium and the Reaction Quotient

• The equilibrium constant (Kₑq) is introduced as a measure of the relative favorability of products versus reactants, with Kₑq values greater than, less than, or equal to 1 indicating different reaction extents.
• The reaction quotient (Q_rx) is presented as a snapshot of the reaction state at any point in time, with its relationship to ΔG given by the equation:
  ΔG=ΔG⁰+RTln⁡Q_rx 

Intrinsic Stability Versus Concentration Effects

• The chapter distinguishes between ΔG⁰, which reflects the intrinsic energy differences (or stability) of reactants and products, and the contribution of reactant/product concentrations.
• Through examples such as the reactions of HCl and acetic acid with water, it is shown that even when starting with equal concentrations, the inherent stability differences drive the reaction to different extents.

Thermodynamics: Enthalpy and Entropy

• The text reviews the first and second laws of thermodynamics, establishing that energy conservation (ΔE = q + w) and the concept of entropy (S) are crucial for understanding reaction spontaneity.
• Enthalpy (ΔH) is discussed in the context of exothermic (ΔH < 0) and endothermic (ΔH > 0) reactions, while entropy changes (ΔS) capture the degree of dispersal or "spread" of energy and matter.
• The Gibbs free energy equation, ΔG=ΔH−TΔS, is derived and emphasized as a critical tool for predicting whether a reaction will proceed spontaneously.

Integration and Application

• The chapter culminates in the integration of these concepts by showing how both the energetic (enthalpy) and dispersive (entropy) factors combine to determine the overall free energy change of a system.
• Examples like the evaporation of water and the reaction between Ba(OH)₂·8H₂O and NH₄SCN are used to illustrate that even endothermic processes can be spontaneous when accompanied by significant increases in entropy.

In summary, this chapter provides a comprehensive framework for understanding the energetics of biochemical reactions. It equips students with the tools to analyze how free energy, equilibrium, and the interplay between enthalpy and entropy govern the direction and extent of reactions—knowledge that is essential for exploring metabolism and other complex cellular processes.