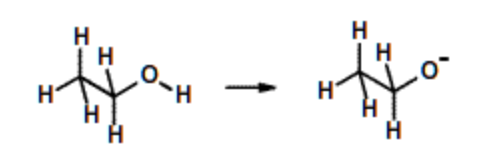Module 3.1: Introduction to pH and Acid Base Behavior
- Page ID
- 24651
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)learning objective
- Understand the relationship between the structure and acidity of an acid.
- Calculate the amount of an acid that is protonated at any given pH.
pH
In solution one water molecule can donate a proton to another. In doing so the first becomes a negatively charged hydroxide ion and the other becomes a positively charged hydronium ion. To simplify things, the hydronium ion is often abbreviated as a bare proton, \(H^+\). The concentration of hydrogen ions in solution can be changed by the addition of an acid (e.g. hydrochloric acid), which will increase the amount of H+. The amount of \(H^+\) can also be decreased by the addition of a base to the solution, such as ammonia.
pH is the measure of the concentration of positively charged hydrogen ions in an aqueous solution. pH stands for \(-log[H^+]\). At low pH, the concentrations of protons is high and the solution is acidic, and, at high pH, the concentrations of protons is low and the solution is basic, due to an abundance of hydronium ions, \(OH^-\). Neutral pH is 7.0. At this pH there are an equal number of \(H^+\) and \(OH^-\) ions in solution. \([H^+]=10^{-7} M\).
pH of various compounds.
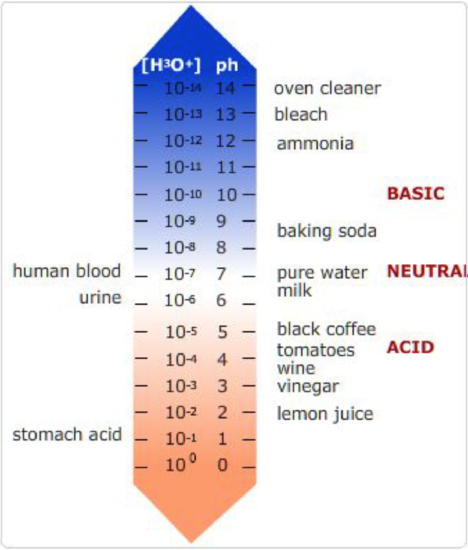
On the left are biological compounds and on the right are some foods and cleaning products.
Acids and Bases
- Acid: can donate protons
- Base: can accept protons
The following describes ionization or dissociation of the proton from the acid:
The acid (HA) donates its proton to a water molecule, generating the conjugate base of the acid (\(A^-\)) and a hydronium ion. Although the released proton (\(H^+\)) is associated with a water molecule, it is often represented in a simpler way as just a free hydrogen ion, \(H^+\).
\[HA +H_2O \rightleftharpoons A^- +H_3O^+\nonumber\]
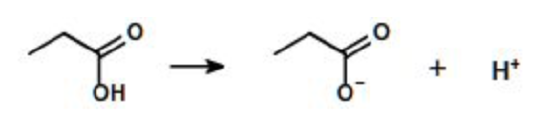
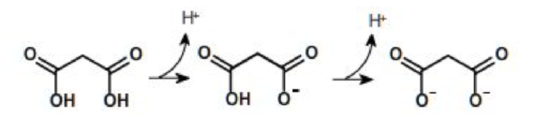
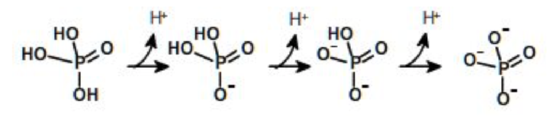
A compound can have one or more ionizable groups, each with different acid strengths. Here are examples of mono-, di-, and triprotic acids.
Monoprotic Acid
Diprotic Acid
Triprotic Acid
General Equilibrium Reactions:
Consider first a very simple reaction and its equilibrium features.
\[A \underset{k_{2}}{\overset{k_1}{\rightleftharpoons}} B\nonumber\]
Kinetics gives the following rate equations:
\[ \frac{d[A]}{d t}=-k_{1}[A]+k_{2}[B] \quad \frac{d[B]}{d t}=k_{1}[A]-k_{2}[B]\nonumber\]
- \(k_1\) is the rate (sec\(^{-1}\)) at which A is converted to B. It is often referred to as the forward rate constant. The overall rate that A goes to B is \(k_1[A]\), giving units of moles/sec.
- \(k_2\) is the rate (sec\(^{-1}\)) at which B is converted to A. It is often referred to as the reverse rate constant. Likewise, the overall rate of the conversion of B to A is \(k^{-1}[B]\), which also has units of moles/sec.
At equilibrium there is no change in the average concentration of A or B, therefore:
\[\begin{array}{l}{\frac{d[A]}{d t}=\frac{d[B]}{d t}=0} \\ {0=-k_{1}[A]_{E Q}+k_{2}[B]_{E Q}} \\ {K_{e q}=\frac{k_{1}}{k_{2}}=\frac{[B]_{E Q}}{[A]_{E Q}}=\frac{[p r o d u c t s]_{E Q}}{[\text {reactants}]_{E Q}}}\end{array}\nonumber\]
The ratio of [B] to [A] at equilibrium is called the equilibrium constant, \(K_{eq}\). It is a constant that is reached at equilibrium regardless of the starting amounts of (A) or (B). The equilibrium constant depends on the relative energy difference between A and B, which may depend on the conditions of the reaction (e.g. temperature)
Characterization of Acid Strength Using \(pK_a\)
When a proton dissociates from the protonated acid (HA), it becomes bound to a water molecule, generating a hydronium ion, in addition to the deprotonated acid (\(A^-\)):
\[H A+H_{2} O \rightleftharpoons A^{-}+H_{3} O^{+}\nonumber\]
Since the concentration of water is essentially constant, it can be ignored and we can write a modified equilibrium reaction that just focuses on the species of interest:
\[H A \rightleftharpoons A^{-}+H^{+}\nonumber\]
and write the equilibrium constant for the dissociation.
\[K_{a}=\frac{\left[H^{+}\right]\left[A^{-}\right]}{[H A]}\nonumber\]
The equilibrium constant for this reaction is given a special name, the 'K-a', or 'K-acidity'. The acidity constant, \(K_a\) is a fundamental property of the acid, it does not depend on the pH of the solution. However, it does depend on the chemical structure and environment of the acidic group. Since the pH scale is used to characterize [\(H^+\)], it is useful to express the acidity constant in the same way, by taking its negative log:
\[\mathrm{pK}_{\mathrm{a}}=\log \mathrm{K}_{\mathrm{a}}\nonumber\]
Strong acids are completely dissociated in water and typically have \(pK_a\) values less than ~ -2. Weak acids do not completely dissociate and have \(pK_a\) values that are equal or greater than 2.0. Examples of strong acids include hydrochloric acid (HCl), and example of a weak acid is acetic acid.
Prediction of Protonation State:
In many cases only one of the two species (protonated or deprotonated) may be biologically active. Given a pH and \(pK_a\) of the ionizable group, we would like to calculate the following:
| The fraction that is protonated: | \(\mathrm{f}_{\mathrm{HA}}=[\mathrm{HA}] / \mathrm{A}_{\mathrm{T}}\) |
| The fraction that is deprotonated: | \(\mathrm{f}_{\mathrm{A}-}=[\mathrm{A}] / \mathrm{A}_{\mathrm{T}}\) |
because this would allow one to predict the biological activity of the system at different pH values. For example, if the protonated species is active, then the activity will be proportional to the fraction that is protonated.
The relationship between the pH, strength of the acid, and the fraction protonated/deprotanated can be obtained from the Henderson-Hasselbalch equation, which is derived below:
\[\begin{array}{l}{K_{a}=\frac{\left[H^{+}\right]\left[A^{-}\right]}{[H A]}} \\ {-\log K_{a}=-\log \left\{\frac{\left[H^{+}\right]\left[A^{-}\right]}{[H A]}\right\}} \\ {-\log K_{a}=-\log \left[H^{+}\right]-\log \left\{\frac{\left[A^{-}\right]}{[H A]}\right\}} \\ {p K_{a}=p H-\log \left\{\frac{\left[A^{-}\right]}{[H A]}\right\}} \\ {p H=p K_{a}+\log \left\{\frac{\left[A^{-}\right]}{[H A]}\right\}}\end{array}\nonumber\]
Note: when pH=\(pK_a\) the concentration of the protonated and deprotonated species are equal (\([A^-] = [HA]\)), when the pH = \(pK_a\) the acid is 50% protonated.
The Henderson-Hasselbalch equation can be used to easily find the fraction protonated and deprotonated. Beginning with defining R=[A-]/[HA] and then writing equations for fraction deprotonated (\(f_{A-}\)) and fraction protonated (\(f_{HA}\)):
\[\begin{array}{l}{R=\frac{\left[A^{-}\right]}{[H A]}} \\ {f_{A^{-}}=\frac{\left[A^{-}\right]}{[H A]+\left[A^{-}\right]} \quad f_{H A}=\frac{[H A]}{[H A]+\left[A^{-}\right]}} \\ {f_{A^{-}}=\frac{\left[A^{-}\right] /[H A]}{[H A] /[H A]+\left[A^{-}\right] /[H A]} f_{H A}=\frac{[H A] /[H A]}{[H A][H A]+[A-] /[H A]}} \\ {f_{A^{-}}=\frac{R}{1+R} \quad f_{H A}=\frac{1}{1+R}}\end{array}\nonumber\]
The value of R is obtained from the given pH and the known \(pK_a\):
\[\begin{array}{l}{R=\frac{\left[A^{-}\right]}{[H A]}} \\ {p H=p K_{a}+\log \left(\frac{\left[A^{-}\right]}{[H A]}\right)} \\ {p H=p K_{a}+\log (R)} \\ {p H-p K_{a}=\log (R)} \\ {10^{(p H-p K a)}=R}\end{array}\nonumber\]
Example Calculation: Calculate the fraction protonated for the side chain of histidine, given that the \(pK_a\) is 6.0
Histidine sidechain ionization
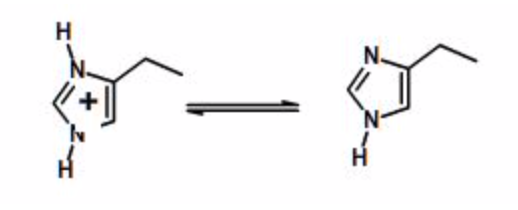
| pH | \(R=10^{(pH-pK_a)}\) | \(F_{HA}=1/(1+R)\) |
|---|---|---|
| 4 | \(R=10^{(4-6)}=10^{-2}\) | \(F_{HA}=1/(1+0.01)=0.99\) |
| 5 | \(R=10^{(5-6)}=10^{-1}\) | \(F_{HA}=1/(1+0.10)=0.91\) |
| 6 | \(R=10^{(6-6)}=10^{0}\) | \(F_{HA}=1/(1+1)=0.5\) |
| 7 | \(R=10^{(7-6)}=10^1\) | \(F_{HA}=1/(1+10)=0.1\) |
| 8 | \(R=10^{(8-6)}=10^2\) | \(F_{HA}=1/(1+100)=0.01\) |
learn by doing
To further explore the relationship between pH and \(pK_a\) and protonation state, complete the following learn by doing.
Let’s look at the relationship’s that exist between the original HA concentrations, the pH of the acid, and the acid’s K value.
1. Using the information provided in the chart to the right as the HA original concentration increases what happens to the K value?
a. increases
b. stays the same
c. decreases
- hint
-
Look at the middle column of the box for the K values.
- Answer
-
b. (the ratio of products to reactants does not change for a given substance at equilibrium.)
2. Using the information provided in the chart to the right as the HA original concentration increases what happens to the pH value?
a. increases
b. stays the same
c. decreases
- hint
-
Look at the right column of the box for the pH values.
- Answer
-
c (as the HA concentration increases more H+ ions are created making the solution more acidic.)
3. In the previous simulations you determined that the pH does not affect the equilibrium constant for the ionization of a weak acid. In this exercise you will determine how pH affects how much of the weak acid is ionized.
Using the equation for fraction protonated shown on the right, you are to select a given pH then calculate the fraction protonated using the concentrations of the various species given in the boxes. Enter your answer into the appropriate location in the data table. Do all five pH values.
Time saver: The total concentration of the weak acid, [HA]+[A-] doesn't change with pH, and is 1000 in this exercise.
As the pH increases
a. [HA] gets smaller as pH gets larger.
b. [HA] gets larger as pH gets larger.
- hint
-
Using the formula above the data chart, select each pH value and calculate the fraction protonated by filling in the values for [HA] and [A-]
- Answer
-
a.
4. Does your graph match the theoretical graph?
a. Yes
b. No
- hint
-
Go back to the "fraction protonated calculation"
- Answer
-
a. (Good Job!)
5. At what point does the fraction protonated equal 0.5?
a. pH 1.
b. pH 4.
c. pH 6.
- hint
-
Look at how the graph changes with pH and how this changes the fraction.
- Answer
-
b. (when the curve is at its midpoint the fraction protonated is .5. This also means the fraction deprotonated is also .5.)
6. What does the midpoint of the curved graph tell you about the acid?
a. \(pK_a) of the acid
b. Concentration of the HA
- hint
-
Remember that at this point you have a 50-50 mix of protonated and deprotonated.
- Answer
-
a. (the \(pK_a\) of the acid is the point that you have a 50-50 mix of protonated and deprotonated.)
Now that you have completed the previous activity on weak acids, try applying what you have learned to this real life example.
did i get this
1. Aspirin will more rapidly cross membranes when it is uncharged (protonated). This learn-by-doing explores the effect of pH on aspirin uptake.
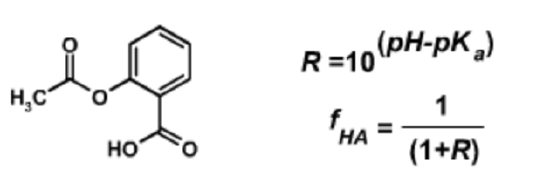
The structure of aspirin (acetylsalicyclic acid) is shown above (left). The carboxylate group has a \(pK_a\) of 4.0.
The pH of the stomach is 2.0 what is the fraction of aspirin that is protonated in the stomach (the right-hand equations may be helpful)?
a. 0.99
b. 0.90
c. 0.09
- hint
-
The right-hand equations may be helpful
- Answer
-
a. (pH=2, \(pK_a\)=4, \(R=10^{2-4}=10^{-2}\space f_{HA}=\frac{1}{(1+0.01)}=0.99\))
2. What does the midpoint of the curved graph tell you about the acid?
a. \(pK_a) of the acid
b. Concentration of the HA
- hint
-
Remember that at this point you have a 50-50 mix of protonated and deprotonated.
- Answer
-
a. (the \(pK_a\) of the acid is the point that you have a 50-50 mix of protonated and deprotonated.)
3. What does the midpoint of the curved graph tell you about the acid?
a. \(pK_a) of the acid
b. Concentration of the HA
- hint
-
Remember that at this point you have a 50-50 mix of protonated and deprotonated.
- Answer
-
a. (the \(pK_a\) of the acid is the point that you have a 50-50 mix of protonated and deprotonated.)
4. What does the midpoint of the curved graph tell you about the acid?
a. \(pK_a) of the acid
b. Concentration of the HA
- hint
-
Remember that at this point you have a 50-50 mix of protonated and deprotonated.
- Answer
-
a. (the \(pK_a\) of the acid is the point that you have a 50-50 mix of protonated and deprotonated.)
Chemical Structure and Acidity:
The equilibrium constant, Keq, for any reaction is related to the energy difference between reactants (e.g. [HA]) and products (e.g. [A-]), by the well-known formula:
\[\begin{array}{l}{E_{A^{-}}-E_{H A}=\Delta G^{0}=-R T \ln K_{a}} \\ {K_{a}=e^{-\left(E_{A-}-E_{H A}\right) / R T}} \\ {K_{a}=e^{-\Delta G^{0} / R T}}\end{array}\nonumber\]
(R = gas constant, 8.31 J/mol-K, RT=2.5 kJ/mol @300K).
The following table explores the relationship between structure and acidity.
| Dissociation Reaction | Acid Strength/AA type | Explanation of Acidity |
|---|---|---|
|
|
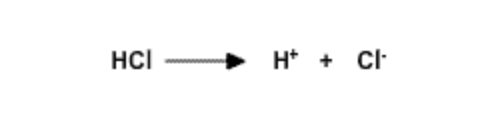
Hydrochloric Acid, \(pK_a\) = -20 | Strong acid because ions interact with water. Complete dissociation. |
|
|
Ethanol, \(pK_a\)= 14. (Amino acids serine & threonine) | Very weak acid. Little ionization of the -OH group. |
|
|
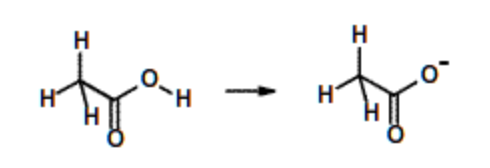
Acetic acid, \(pK_a\) = 4. (Amino acids aspartate & Glutamate) | Weak acid, but stronger than ethanol due to the charge delocalization over carbonyl group. |
|
|
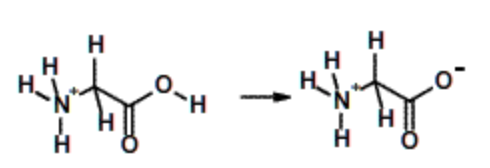
Glycine, \(pK_a\) = 2. (All amino acids) | Weak acid, but stronger than acetic due to charge delocalization over carbonyl group and positively charged nitrogen. |
did i get this
1. The structure of trifluoroacetic acid (TFA, \(pK_a\)=0.5) and acetic acid (\(pK_a\)=4.8) are shown below. Which is the stronger acid, TFA or acetic acid?
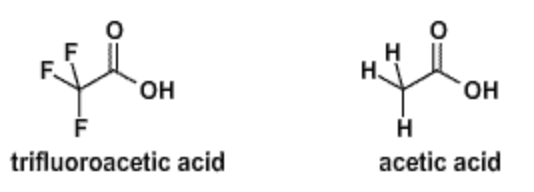
a. TFA is the stronger acid
b. Acetic acid is the stronger acid
- hint
-
\(pK_a\)=-log\(K_a\). Small \(pK_a\) values indicate large or small \(K_a\) values?
A stronger acid ionizes more completely, indicating a larger acidity constant, \(K_a\).
- Answer
-
a. (The acid with the lower \(pK_a\) is the stronger acid.)
2. Explain why TFA is a stronger acid than acetic acid.
- hint
-
How do fluorine atoms differ from hydrogen atoms?
- Answer
-
When either of the two acids deprotonate, a negative charge is generated on the COOH group. The more electronegative fluorine atoms withdraw, and therefore delocalize, some of that charge, which lowers the energy of the deprotonated state, enhancing ionization.
Review Quiz
did i get this
1. Upon losing a proton, an acid becomes
a. highly reactive
b. its conjugate acid.
c. its conjugate base.
d. a hydronium ion.
e. a hydroxide ion.
- answer
-
c.
2. One factor affecting the strength of an acid is
a. frequent exercise.
b. the electronegativity of atoms near the acidic group.
c. the number of double bonds.
d. the number of protons released.
e. none of the above.
- answer
-
b.
3. If the \(pK_a\) of trifluoracetic acid (TFA) is 0, and the \(pK_a\) of acetic acid is 4.0, the \(pK_a\) of trichloroacetic acid (TCA) is:
a. -1
b. 1
c. 3
- hint
-
Try the exercise on the page comparing TFA to acetic acid.
- answer
-
b. (Because chlorine is less electronegative than fluorine, TCA is a weaker acid than TFA and the \(pK_a\) of TCA will be closer to TFA.)
4. When the pH is lower than the \(pK_a\), then
a. The concentration of [HA] exceeds [A-].
b. The concentration of [HA] is less than [A-].
c. The concentration of [HA] is equal to [A-].
d. The ratio of [HA] to [A-] cannot be determined.
e. The concentration of the acid is required to calculate the ratio of [HA] to [A-].
- hint
-
The \(pK_a\) marks the pH that will 1/2 protonate the acid. How will lowering the pH affect the hydrogen ion concentration?
- answer
-
a. (The \(pK_a\) marks the 1/2 point in the effect of proton concentration of an acid. If the pH is less than \(pK_a\), then [HA]>[A-], if the pH > \(pK_a\), then [HA] is less than [A-].)