Solutions March 20, 2007, Final Exam
- Page ID
- 6963
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\[\mathrm{BioSci\: 102-02\\ Mar.\: 20,\: 2007,\: Final Exam}\]
Instructions:
• There are nine pages in this exam including the cover sheet, please count them before you start to make sure all are present.
• Write your name on each page of the exam.
• Write your answers in the space provided below each question. If you need more space use the back of the page and indicate clearly that you have continued your answer on the back. Do not use additional paper. For calculation problems a clear line of calculations leading to your final answer must be shown to obtain full credit.
Use the following \(\mathrm{pK_{a}}\) values for the exam.
| Amino Acid | \(\mathbf{\alpha -NH_{2}}\) | \(\mathbf{\alpha -COOH}\) | R-group |
|---|---|---|---|
| Ala, Gly, Ile, Leu, Val | 9.7 | 2.3 | \(-\) |
| Asn, Gln | 9.0 | 2.1 | \(-\) |
| Met, Ser, Trp | 9.3 | 2.3 | \(-\) |
| Phe | 9.1 | 1.8 | \(-\) |
| Pro | 10.6 | 2.0 | \(-\) |
| Thr | 10.4 | 2.6 | \(-\) |
| Asp | 9.8 | 2.1 | 3.9 |
| Glu | 9.7 | 2.2 | 4.2 |
| His | 9.2 | 1.8 | 6.0 |
| Cys | 10.8 | 1.8 | 8.3 |
| Tyr, Lys | 9.1 | 2.2 | 10.0 |
| Arg | 9.0 | 2.2 | 12.5 |
\(\begin{matrix} \mathrm{log\: 1.0=0.00}\\ \mathrm{log\: 1.5=0.18} \\ \mathrm{log\: 2.0=0.18}\\ \mathrm{log\: 2.5=0.40}\\ \mathrm{log\: 3.0=0.48}\\ \mathrm{log\: 3.5=0.54}\\ \mathrm{log\: 4.0=0.60}\\ \mathrm{log\: 4.5=0.65}\\ \mathrm{log\: 5.0=0.70}\\ \mathrm{log\: 5.5=0.74}\\ \mathrm{log\: 6.0=0.78}\\ \mathrm{log\: 6.5= 0.81}\\ \mathrm{log\: 7.0=0.85}\\ \mathrm{log\: 7.5=0.88}\\ \mathrm{log\: 8.0=0.90}\\ \mathrm{log\: 8.5=0.93}\\ \mathrm{log\: 9.0=0.95}\\ \mathrm{log\: 9.5=0.98}\\ \mathrm{log\: 10.0=1.00} \end{matrix}\)
\(\mathbf{R=8.3\times 10^{-3}\: kJ/ ^{\circ}K\cdot mol}\)
\(\mathbf{25^{\circ}C=298K}\)
| Question | Value | Score |
|---|---|---|
| 1 | 16 | |
| 2 | 15 | |
| 3 | 20 | |
| 4 | 14 | |
| 5 | 11 | |
| 6 | 14 | |
| 7 | 16 | |
| 8 | 36 | |
| 9 | 10 | |
| 10 | 14 | |
| 11 | 22 | |
| 12 | 12 | |
| Total | 200 |
1. For the following questions mark an "X" in the blank next to the most correct answer to the question (one answer for each question).
a). (4) An important class of enzyme inhibitors are transition state analogs. These inhibitors resemble the high-energy transition state that is stabilized by an enzyme. What class of inhibitor would a transition state analog most likely fall into?
Tetrahedral.
Uncompetitive.
Allosteric.
Non-competitive.
X Competitive. (it would bind to the active site and prevent S binding)
b) (4) A benefit of measuring the initial rate of an enzyme catalyzed reaction, \(\mathrm{V_{i}}\), is that at the beginning of a reaction:
X Changes in [S] are negligible, so [S] can be treated as a constant.
[ES] can be measured accurately.
\(\mathrm{V_{i}=V_{max}}\)
Changes in \(\mathrm{K_{m}}\) are negligible, so \(\mathrm{K_{m}}\) can be treated as a constant.
Varying [S] has no effect on \(\mathrm{V_{i}}\).
c) (4) A homotetrameric enzyme, E, has four identical binding sites for substrate S, and exhibits positive cooperative binding of substrate S. Which of the following is least likely to be true of E?
There are disulfide bonds between the subunits of E.
The reaction catalyzed by E exhibits a sigmoidal dependence on [S].
X The \(\mathrm{K_{m}}\) of E for S is increased by S binding.
This is essentially the definition of positive cooperativity.
Other factors bind to and regulate the activity of E.
\(\mathrm{V_{max}=k_{cat}[E_{t}]}\).
d) (4) For the enzyme catalyzed reaction:
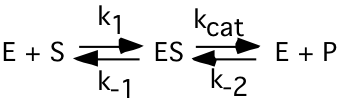
The expression that best defines the Michaelis-Menten constant (\(\mathrm{K_{m}}\)) for this reaction using the initial rates and steady-state assumptions (as used in class) is:
\(\mathrm{K_{m}=\dfrac{[E]\cdot [S]}{[ES]}}\)
\(\mathrm{K_{m}=\dfrac{k_{-1}}{k_{1}}}\)
\(\mathrm{K_{m}=\dfrac{d[P]}{dt}}\)
\(\mathrm{K_{m}=\dfrac{k_{-1}+k_{1}}{k_{cat}}}\)
X \(\mathrm{K_{m}=\dfrac{k_{-1}+k_{cat}}{k_{1}}}\)
2. An enzyme, E, catalyzes the reaction A B leading to a \(10^{9}\)-fold increase in the reaction rate. Relative to the uncatalyzed reaction, what effect does the enzyme have on each of the following? Use "U" for unchanged, "I" for increased, "D" for decreased, and "N" for need more information. (3 pts. each).
[B] at equilibrium U
\(\mathrm{\Delta G \ddagger}\) (activation energy) for the reaction \(\mathrm{A\Rightarrow B}\) D
\(\mathrm{\Delta H}\) for the reaction \(\mathrm{A \Rightarrow B}\) U
\(\mathrm{\Delta G^{\circ’}}\) for the reaction \(\mathrm{B \Rightarrow A}\) U
\(\mathrm{\Delta G}\) for the reaction \(\mathrm{A \Rightarrow B}\) if [A] < [B] U
3. The active ingredients of some chemical weapons are inhibitors of the enzyme acetylcholinesterase (ACHE). A U. C. researcher was provided with blood samples (identified with codes, “UPI, and “AP”) from two groups of individuals and was asked to determine if either group had been exposed to ACHE inhibitors. The researcher was also provided with blood from people known not to have been exposed (“Control”). Protein gels showed that the amount of ACHE protein did not differ between the three blood samples. Because the groups were fairly large, there was little possibility that any sample would contain a significant level of any mutant form of ACHE. Measurement of the activity of ACHE in the blood samples at various substrate concentrations produced linear Lineweaver-Burk plots that were used to determine the values in the table below.
\[\begin{matrix} \mathbf{\underline{Sample\: Code}} & \mathbf{\underline{Observed\: Km}} & \mathbf{\underline{Observed\: Vmax}} \\ \mathrm{Control} & \mathrm{1.0\times 10^{-4}\: M} & \mathrm{6.0\: \mu moles/min\cdot ml} \\ \mathrm{UPI}& \mathrm{1.0\times 10^{-4}\: M} & \mathrm{2.0\: \mu moles/min\cdot ml} \\ \mathrm{AP} & \mathrm{ 0.5\times 10^{-4}\: M} & \mathrm{3.0\: \mu moles/min\cdot ml} \end{matrix}\]
For each statement below indicate (with an X in the appropriate box) if the statement is consistent with the data, inconsistent with the data, or if no evidence concerning the statement is provided by the data ( 4 points each).
| Statement | Consistent | Inconsistent | No evidence |
| The UPI sample contains a noncompetitive inhibitor of ACHE. | X | ||
| The AP sample contains a competitive inhibitor of ACHE. | X | ||
| An inhibitor is present at a higher concentration in the UPI sample then in the AP sample | X | ||
| The ACHE enzyme in both the UPI and AP samples exhibited hyperbolic kinetics. | X | ||
| The apparent \(\mathrm{k_{cat}}\) for the AP sample is higher than that of the UPI sample | X |
- UPI \(\mathrm{K_{m}}\) unchanged, but \(\mathrm{V_{max}}\) decreased relative to control
- AP has decreased \(\mathrm{K_{m}}\) and \(\mathrm{V_{max}}\), not competitive inhibitor
- Don’t know \(\mathrm{K_{i}}\) so no way to evaluate [I]
- “linear Lineweaver-Burk plots” stated in the problem indicates hyperbolic kinetics
- In AP sample \(\mathrm{V_{max}}\) is decreased, but \(\mathrm{[E_{t}]}\) stated to be unchanged in problem, so there is an apparent decrease in \(\mathrm{k_{cat}}\), because \(\mathrm{V_{max}=k_{cat}[E_{t}]}\)
Will include only the -2 and -3 forms of phosphate, so pH will be near 12.3 let “x” = fraction in -2 form, then 1-x = fraction in -3 form. This gives:
\[\mathbf{-2x + -3(1-x) = -2.6}\]
\[\mathbf{-2x -3 +3x = -2.6}\]
\(\mathbf{x = -2.6 + 3 = 0.4}\) ; so -2 form present at 0.4 of total, -3 form present at 1-0.4 = 0.6 of total.
\[\mathbf{pH = pK_{a} + log (-3 form/-2 form) = 12.3 + log (0.6/0.4) = 12.48}\]
pH = 12.48
5. You are working on an enzyme that has a reactive histidine residue at the active site. For this enzyme to effectively catalyze the reaction the histidine must be in the unprotonated state. This particular histidine residue has a \(\mathrm{pK_{a}}\) of 5.0 due to the proximity of the side chain of another amino acid residue in the protein structure.
a) (3) Write the one and three letter codes for an amino acid residue whose proximity to the histidine discussed above could cause the indicated change in the \(\mathrm{pK_{a}}\) of the histidine.
R, Arg or K, Lys (the strong + charge would inhibit the His from taking on a similar + charge)
b) (8) Making the assumption that the ionization state of the histidine residue is the only pH-responsive determinant of the activity in this enzyme, what fraction of the enzyme would be active at pH 5.3?
\[\mathbf{5.3 = 5.0 + log (His^{\circ}/His^{+})}\]
\[\mathbf{0.3 = log (His^{\circ}/His^{+})}\]
\[\mathbf{(His^{\circ}/His^{+}) = 2, His^{\circ} = 2His^{+}}\]
So it is 2/3 \(\mathbf{His^{\circ}}\) and 1/3 \(\mathbf{His^{+}}\)
Only the \(\mathbf{His^{\circ}}\) form is active so 2/3 or 67% of enzyme is active
fraction active = 0.67
6. An important step in metabolism is the splitting of fructose-1,6-bisphosphate (F1,6BP) into two three carbon compounds; glyceraldehyde-3-phosphate (G3P) and dihydroxyacetone phosphate (DHAP):
\[\mathrm{F1,6BP \Leftrightarrow G3P + DHAP\: \Delta G^{\circ’}=+24\: kJ/mol\: @25^{\circ}C}\]
a) (2) Under standard state conditions (the conditions at which \(\mathrm{\Delta G ^{\circ’}}\) is defined) in which direction will the reaction proceed? (circle one)
Forward \(\mathrm{\fbox{Reverse}}\) positive \(\mathbf{\Delta G^{\circ’}}\)
b) (10) The concentrations of the products and reactants were measured in a liver cell and found to be:
\(\mathrm{[F1,6BP]=40\times 10^{-6}\: M}\)
\(\mathrm{[DHAP]=100\times 10^{-6}\: M}\)
\(\mathrm{[G3P]=20\times 10^{-6}\: M}\)
At these concentrations what will the \(\mathrm{\Delta G}\) of the reaction be (\(\mathrm{@\: 25^{\circ}C}\))?
\[\mathbf{\Delta G =\Delta G^{\circ'}+RTln\dfrac{[DHAP][G3P]}{[F1,6BP]}}\]
\[\mathbf{\Delta G=24+8.3\cdot 10^{-3} \cdot 298 ln\dfrac{100\cdot 10^{-6} \cdot 20\cdot 10^{-6}}{40\cdot 10^{-6}}}\]
\[\mathbf{\Delta G=24+8.3\cdot 10^{-3}\cdot 298 ln 5\cdot 10^{-5}}\]
\[\mathbf{\Delta G =24-24.5=-0.50\: kJ/mol}\]
\(\mathrm{\Delta G}\) = -0.50 kJ/mol
(units)
c) (2) On the basis of your answer to part b) which way will the reaction proceed in the liver cell? (circle one)
\(\mathrm{\fbox{Forward}}\) Reverse
7. Below is a graph of a reaction of tubulin in a test tube in the presence of GTP where microtubule polymerization is monitored by measuring light absorbance at 340 nm (A340).

The normal \(\mathrm{k_{cat}}\) for the GTPase activity of the enzymatically active form of \(\beta\)-tubulin is \(\mathrm{0.14\: sec^{-1}}\). Suppose that you identify a mutant form of \(\beta\)-tubulin that changes this enzymatic activity so that the \(\mathrm{k_{cat}}\) is increased to \(\mathrm{1.4\: sec^{-1}}\). The change in the \(\mathrm{k_{cat}}\) is the only change in this tubulin, all other properties remain the same.
a) For each of the following, circle “D” for decrease, “I” for increase, or “N” for no change based on the effect that the mutation would have on the indicated value in the microtubule assembly reaction relative to the wild-type enzyme (3 each).
\(\mathbf{\fbox{D}\:\:\:\:\: I\:\:\:\:\: N\:\:\:\:\:}\)The length of the “GTP cap” at the + end of microtubules.
\(\mathbf{\fbox{D}\:\:\:\:\: I\:\:\:\:\: N\:\:\:\:\:}\)The average time after incorporation of a tubulin dimer onto the “+”-end of a microtubule that it completes the hydrolysis of GTP.
\(\mathbf{D\:\:\:\:\: I\:\:\:\:\: \fbox{N}\:\:\:\:\:}\)The affinity of the head group of kinesin motor protein for a microtubule when the motor protein has ADP bound.
\(\mathbf{\fbox{D}\:\:\:\:\: I\:\:\:\:\: N\:\:\:\:\:}\)The average length of a microtubule in the plateau phase of the reaction.
b) (4) On the plot above, sketch the curve that you would expect if the mutant ß-tubulin was used in a microtubule assembly experiment that otherwise was the same as the experiment performed on normal tubulin.
More rapid loss of GTP form of tubulin would lead to increased frequency of complete loss of GTP cap at +-end and more frequent catastrophic depolymerization of microtubles from both ends.
8. True-False: For each of the following statements circle the "T" if the statement true or the "F" if the statement is false. (3 points each).
\(\mathbf{T\:\:\:\:\: \fbox{F}\:\:\:\:\:}\)Hemoglobin would likely run more slowly on an SDS polyacryalmide gel in the absence of \(\beta\)-mercaptoethanol than in the presence of this compound.
\(\mathbf{\fbox{T}\:\:\:\:\: F\:\:\:\:\:}\)Lysine would bind more tightly to a sulfonated polystyrene column at pH7 than would glycine. (negative column binds positive AA)
\(\mathbf{\fbox{T}\:\:\:\:\:F\:\:\:\:\:}\)A serine residue can interfere with formation of an alpha-helix in a protein because it can form a hydrogen bond with itself.
\(\mathbf{T\:\:\:\:\:\fbox{F}\:\:\:\:\:}\)A covalent bond will always have greater bond energy than 40 hydrogen bonds.
\(\mathbf{T\:\:\:\:\:\fbox{F}\:\:\:\:\:}\)Membranes commonly include free fatty acids.
\(\mathbf{T\:\:\:\:\:\fbox{F}\:\:\:\:\:}\)Enzymes only change hydrogen bonds and other weak interactions in converting substrates to products because covalent bonds are too high energy to be altered at biological temperatures.
\(\mathbf{T\:\:\:\:\:\fbox{F}\:\:\:\:\:}\)The role of protein kinases is to activate enzymes. (can also inactivate)
\(\mathbf{\fbox{T}\:\:\:\:\:F\:\:\:\:\:}\)Proteolytic activation of enzyme activity can help produce a spatial separation between enzyme synthesis and enzyme activation.
\(\mathbf{T\:\:\:\:\:\fbox{F}\:\:\:\:\:}\)Due to the presence of a trans double bond, sphingolipids have higher melting points than do glycerolipids.
\(\mathbf{\fbox{T}\:\:\:\:\:F\:\:\:\:\:}\)Prosthetic groups bind more tightly to enzymes than do coenzymes.
\(\mathbf{T\:\:\:\:\:\fbox{F}\:\:\:\:\:}\)All cofactors include carbon atoms. (Can be metal ions)
\(\mathbf{T\:\:\:\:\:\fbox{F}\:\:\:\:\:}\)An increase in the concentration of CO2 in blood would cause hemoglobin to release BPG.
9. (10) A competitive inhibitor with \(\mathrm{K_{i}=2\:\mu M}\) is added to an enzymatic reaction at a concentration of \(\mathrm{[I]=18\: \mu M}\). \(\mathrm{K_{m}=4\: mM}\) for the substrate of this enzyme. At what substrate concentration would the reaction in the presence of the inhibitor be inhibited 80 % relative to the uninhibited reaction?
\[\mathbf{V_{inhib}=0.2V}\]
\[\mathbf{\dfrac{V_{max}[S]}{K_{m}(1+\dfrac{[I]}{K_{i}})+[S]}=0.2\dfrac{V_{max}[S]}{K_{m}+[S]}(can\: cancel\: "V_{max}[S]"\: on\: both\: sides)}\]
\[\mathbf{K_{m}+[S]=0.2(K_{m}(1+\dfrac{[I]}{K_{i}})+[S])}\]
\[\mathbf{5K_{m}+5[S]=K_{m}(1+\dfrac{[I]}{K_{i}})+[S]}\]
\[\mathbf{5\cdot 4+4[S]=4(1+\dfrac{18}{2})}\]
\[\mathbf{20+4[S]=40;\: 4[S]=20}\]
\[\mathbf{[S]=5\: mM}\]
[S] = 5 mM
units
10. (14) An enzyme was assayed at various substrate concentrations and the following initial velocity data were collected. Plot the data on a Lineweaver-Burk (double reciprocal) plot on the axes provided. Use the plot to determine the \(\mathrm{V_{max}}\) and the \(\mathrm{K_{m}}\) for this enzymatic reaction.
| S (mM) | V (nm/ml\(\cdot\)sec) |
|---|---|
| 1.25 | 2.05 |
| 2.00 | 2.75 |
| 2.50 | 3.33 |
| 5.00 | 5.0 |
| 10 | 6.8 |
| 20 | 8.0 |
| 0.8 | 0.49 |
| 0.5 | 0.36 |
| 0.4 | 0.30 |
| 0.2 | 0.20 |
| 0.1 | 0.147 |
| 0.05 | 0.125 |

\(\mathbf{1/V_{max}=0.1,\: V_{max}=10\:\:\:\:\: -1/K_{m}=-0.2,\: K_{m}=5}\)
\(\mathbf{V_{max}=\underline{10\: nmol/ml\cdot sec} \:\:\:\:\: K_{m}=\underline{5\: mM}}\)
11. A hexapeptide was identified in the venom of a spider found in a trashcan outside of the ARC on the UC Davis campus. Amino acid analysis showed that the peptide contained amino acids in the following ratio: 2 Glx (either Glu or Gln, the amino acid analysis could not differentiate), 1 Arg, 1 Ser, 1 Met, 1 Phe. A set of experiments were performed to determine the sequence of the oligopeptide. Briefly state the conclusion(s) you can draw from each of the individual experiments below, and use the information to write the sequence of the oligopeptide in the spaces at the bottom.
a) (4) Treatment of the oligopeptide with Sanger’s reagent (FDNB) resulted in formation of DNP serine.
This tells me: Ser is the N-terminal AA
b) (4) Treatment of the oligopeptide with chymotrypsin led to release of free methionine.
This tells me: Met is C-terminal AA and is preceded by Phe
c) (8) Treatment of the oligopeptide with trypsin led to production of two tripeptides. At pH7, both products had a net neutral charge.
This tells me: Arg must be third AA, must be preceded by a Glu (to make peptide have 0 charge) and following residue must be Gln (so other peptide will not be charged
(for full credit give sequence in one letter code!)
(6) Sequence: S E R Q F M
(Did you remember to use the one letter code?)
12 (12) Difluoromethylornithine (DFMO) is an irreversible inhibitor that covalently binds to and inactivates the enzyme ornithine decarboxylase (ODC) that has the novel amino acid ornithine as its substrate. This inhibitor may be effective against the parasite that causes sleeping sickness. You are studying the effects of DFMO on ODC. Earlier tests had shown that for ODC and ornithine the \(\mathrm{K_{m}=2\: mM}\). You assay a preparation of ODC with 3 mM ornithine as the substrate and measure a reaction velocity of \(\mathrm{2\: \mu M/min}\) of product formed. You carry out a similar reaction, but in this case you have added 3 nM DFMO. Under the conditions used, DFMO reacts quantitatively with ODC (i. e. each molecule of DFMO inactivates one molecule of ODC). You find that in the presence of the inhibitor (DFMO) the reaction velocity is \(\mathrm{1\: \mu M/min}\) of product formed.
Using the above information, determine the \(\mathrm{k_{cat}}\) of the ODC under these conditions when no inhibitor is present.
\[\mathbf{V_{max}=k_{cat}\cdot [E_{t}],\: so\: k_{cat}=V_{max}/[E_{t}]\: so\: you\: need\: to\: find\: V_{max}\: and\: [E_{t}]}\]
\[\mathbf{V=\dfrac{V_{max}[S]}{K_{m}+[S]}}\]
\[\mathbf{2=\dfrac{V_{max}\cdot 3}{2+3}; \: V_{max}=\dfrac{2\cdot 5}{3}=3.33\: \mu M/min}\]
3 nM DFMP decreases velocity by \(\mathbf{\dfrac{1}{2}}\) so it must be inactivating \(\mathbf{\dfrac{1}{2}}\) of the ODC. (This is because the [S] and \(\mathbf{K_{m}}\) do not change with addition of DFMP, so \(\mathbf{V_{max}}\) must be changing, but \(\mathbf{V_{max}=k_{cat}[E_{t}]}\), since \(\mathbf{k_{cat}}\) is not changing, \(\mathbf{[E_{t}]}\) must decrease by half for \(\mathbf{V_{max}}\) to decrease by this factor, so [DFMP] = 0.5[ODC])
Therefore:
\(\mathbf{0.5\: [ODC_{t}]=3\: nM}\)
\(\mathbf{[ODC_{t}]=2\cdot 3\: nM=6\: nM}\)
\(\mathbf{k_{cat}=(3.33\times 10^{-6}\: M/min)/6\times 10^{-9}\: M=556\: min^{-1}\: (or\: 9.26\: sec^{-1})}\)
\(\mathrm{k_{cat}}=\underline{\mathbf{556\: min^{-1}}}\)
units

