Solutions for Sample Midterm 1
- Page ID
- 6244
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\[\mathbf{BioSci\: 102, \\Sample\: Study\: Problems\: for\: First\: Midterm}\]
1. What two factors determine how "good" (i. e. effective) a particular buffer solution is for maintaining a given pH?
a) How close the given pH is to the \(\mathrm{pK_{a}}\) of the buffering agent (the closer the better).
b) The concentration of the buffering agent.
2. The following question has two parts.
a) What is the final pH of a solution obtained by mixing 250 ml of 0.3 M acetic acid with 300 ml of 0.2 M KOH? (\(\mathrm{pK_{b}}\) of acetate = 9.24). (Show your work!)
Moles of acetic acid = \(\mathbf{0.25 l \times 0.3\: M}\) = 0.075 moles
Adding \(\mathbf{0.3 l \times 0.2\: M}\) = 0.06 moles of \(\mathbf{OH^{-}}\) to this solution will convert 0.06 moles of acetic acid to 0.06 moles of acetate, 0.015 moles of protonated acetic acid will remain.
\[\mathbf{pK_{a}= 14 - pK_{b} = 14 - 9.24 = 4.76}\]
\[\mathbf{pH = pK_{a} + log \dfrac{[CH_{3}CO_{2}^{-}]}{[CH_{3}CO_{2}H]}}\]
\[\mathbf{= 4.76 + log \dfrac{0.06\: moles/ 0.551}{0.015\: moles/ 0.551}}\]
\[\mathbf{= 4.76 + log \dfrac{0.06\: moles}{0.015\: moles}}\]
\[\mathbf{= 5.36}\]
\[\mathbf{pH = 5.36}\]
b) What is the net charge on the acetic acid/acetate molecules at this pH?
Since acetic acid is neutral, the net charge is determined by the fraction of the moleucles in the negatively charged acetate form.
\[\mathbf{\dfrac{moles\:of\:acetate}{total\:mole\:of\:acetate\:and\:acetic\:acid}=\dfrac{0.06\:moles}{0.075\:moles} = 0.8}\]
\[\mathbf{net\: charge = 0.8 \times -1 = -0.8}\]
3. Explain how you would make 2 liters of a 0.015 M buffer at pH 4.4 using crystalline disodium glutamate (MW = 191) and 0.9 M HCl. (use pKa values: \(\alpha\)-COOH = 2.2, side chain = 4.2, and \(\alpha\)-NH2 = 9.7).
\[\mathbf{Glu^{+}\begin{matrix} \Leftrightarrow\\ pK_{a1}=2.2 \end{matrix} Glu^{0} \begin{matrix} \Leftrightarrow\\ pK_{a2}=4.2 \end{matrix} Glu^{-} \begin{matrix} \Leftrightarrow\\ pK_{a3}=9.7 \end{matrix} Glu^{2-}}\]
pH = 4.4 so only \(\mathbf{Glu^{0}}\) and \(\mathbf{Glu^{-}}\) will be present in significant concentrations
(0.015 M) (2 l) = 0.03 moles of Glu total \(\mathbf{\times}\) 191 g/mol = 5.73 g \(\mathbf{Na_{2}Glu}\)
\[\mathbf{pH = pK_{a} + log \dfrac{[Glu^{-}]}{[Glu^{0}]}}\]
\[\mathbf{4.4 = 4.2 + log \dfrac{[Glu^{-}]}{[Glu^{0}]}}\]
\[\mathbf{0.2 = log \dfrac{[Glu^{-}]}{[Glu^{0}]}}\]
\[\mathbf{\dfrac{[Glu^{-}]}{[Glu^{0}]}= 1.58}\]
\[\mathbf{[Glu^{-}] = 1.58\: [Glu^{0}]}\]
\[\mathbf{Glu^{-} + Glu^{0} = 0.03\: moles}\]
\[\mathbf{2.58 Glu^{0} = 0.03\: moles}\]
\[\mathbf{Glu^{0} = 0.0116\: moles}\]
\[\mathbf{Glu^{-}=0.03-0.0116=0.0184\: moles}\]
Must first convert 0.03 moles of \(\mathbf{Glu^{2-}}\) to 0.03 moles of \(\mathbf{Glu^{-}}\), this will take 0.03 moles of HCl. Then add enough HCl to convert 0.0116 moles of \(\mathbf{Glu^{-}}\) to \(\mathbf{Glu^{0}}\), this takes 0.0116 moles of HCl.
\[\mathbf{Total\: HCl = 0.03 + 0.0116 = 0.0416\: moles}\]
\[\mathbf{\dfrac{0.0416\: moles}{0.9\: mol/l}=0.04621=46.2\: ml\: of\: 0.9\: M\: HCl}\]
4. A protein was completely digested with arg-c (an enzyme which cuts on the C-side of R residues) and an internal peptide (i. e. not derived from the N- or C- terminus) was purified. Determine its sequence from this information and the information given below. (since arg-c cuts after R residues, the last residue must be an R!)
a) Amino acid analysis of one mole of the peptide yields: 3 moles of cysteine, 1 mole of methionine, 3 moles of lysine, 1 mole of arginine and 1 mole of tryptophan.
b) Treatment of the intact peptide with trypsin gave rise to three different products; a dipeptide containing arg and trp, a dipeptide containing lys and cys, and a tripeptide containing cys, met and lys. (WR must be at C-term, so W is residue #8!)
c) When the intact peptide was treated with Sanger's reagent (FDNB) and hydrolyzed with acid the derivatized products were DNP-cysteine and mono-DNP-lysine. (C is n-terminal residue; only side chain, not alpha amino group of lysine modified!)
d) Treatment of the intact peptide with cyanogen bromide produced a pentapeptide containing cys, met, and lys; and a tetrapeptide containing arg, lys, trp and cys.
From b) K comes before W to allow release of WR peptide from trypsin digestion
From d) C comes before K @ position 7 to make up tetrapeptide
From d) M comes before C @ position 6 to allow cyanogen bromide cleavage at the correct spot.
From b) The only unexplained tryptic fragments are CK, therefore the rest of the peptide must consist of a pair of CK repeats.
Sequence = C K C K M C K W R
5. For each part of this question identify all amino acids being described (from among those normally occurring in proteins) by:
1) giving the one and three letter codes that are used to designate it (them) (note: each question may have more than one correct answer, please give them all) and;
2) drawing the full structure (of one correct answer) in the form that would predominate at pH 14.
(Note: pH 14 implies all groups are deprotonated)
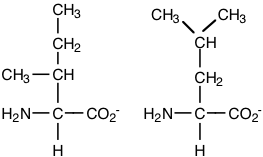
a) An amino acid which is a structural isomer of another amino acid.
I, Ile or L, Leu
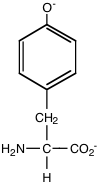
b) An amino acid which can absorb ultraviolet light and which has a side chain which can ionize at physiological pH.
Y, Tyr
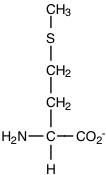
c) An amino acid which is commonly the first amino acid in newly synthesized eukaryotic proteins.
M, Met
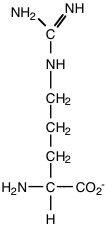
d) The most basic of the 20 common amino acids (i. e. its side chain has the highest pKa value).
R, Arg
6. For the peptide shown below the numbers in parentheses indicate the \(\mathrm{pK_{a}}\) values for the adjacent ionizable groups. Answer the following three questions.
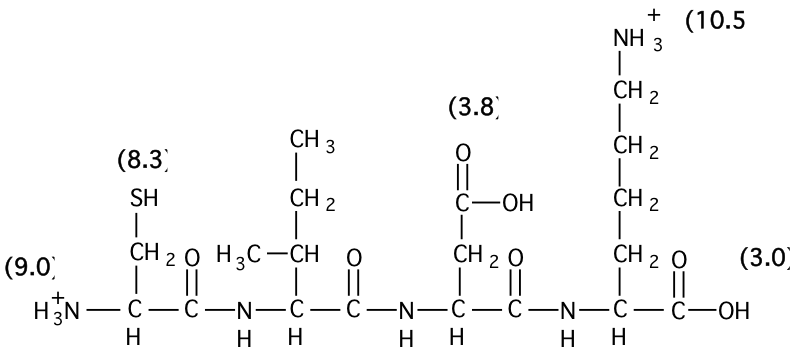
a) Calculate the charge of this peptide (to the nearest 0.1) at pH8.5.
I choose to do it by determining charge on all ionizable groups and adding them up. I number the groups from left to right.
\(\mathbf{Group\: 1:\: 8.5=9+log\dfrac{[-NH_{2}]}{[-NH_{3}^{+}]}}\)
\[\mathbf{\dfrac{[-NH_{2}]}{[-NH_{3}^{+}]}=0.316,\: [-NH_{2}]+[NH_{3}^{+}]=1,\: 0.316[NH_{3}^{+}]+[NH_{3}^{+}]=1}\]
\[\mathbf{[NH_{3}^{+}]=1/1.316=0.76,\: Charge=+1\times 0.76=+0.76}\]
\(\mathbf{Group\: 2: \: 8.5=8.3+log\dfrac{[-S^{-}]}{[-SH]}}\)
\[\mathbf{\dfrac{[-S^{-}]}{[-SH]}=1.58; \: [-SH]=1/2.58=0.39}\]
\[\mathbf{charge=[-S^{-}]\times -1=(1-0.39)\times -1=-0.61}\]
\(\mathbf{Group\: 3: \: fully\: deprotonated,\: charge=-1}\)
\(\mathbf{Group\: 4: \: fully\: protonated,\: charge=+1}\)
\(\mathbf{Group\: 5: \: fully deprotonated, charge=-1}\)
\[\mathbf{ net\: charge= \begin{matrix}Group\: 1 \\ +0.76 \end{matrix} + \begin{matrix} Group\: 2 \\ -0.61 \end{matrix} + \begin{matrix} Group\: 3\\ -1 \end{matrix} + \begin{matrix} Group\:4\\ +1 \end{matrix} + \begin{matrix} Group\: 5\\ -1 \end{matrix} = -0.85}\]
b) Calculate the appproximate pI of this peptide (assume that there are no interactions among the different ionizable groups).
\[\begin{matrix} \mathbf{pep^{+2}} & \mathbf{\Leftrightarrow} & \mathbf{pep^{+1}} & \mathbf{\Leftrightarrow} & \mathbf{pep^{0}} & \mathbf{\Leftrightarrow} & \mathbf{pep^{-1}} & \mathbf{\Leftrightarrow} & \mathbf{pep^{-2}} & \mathbf{\Leftrightarrow} & \mathbf{pep^{-3}} \\ & \mathbf{pK_{a1}=3.0} & \: & \mathbf{pK_{a2}=3.8} & \: & \mathbf{pK_{a3}=8.3} & \: & \mathbf{pK_{a4}=9.0} & \: & \mathbf{pK_{a5}=10.5} \end{matrix}\]
\[\mathbf{pep^{0}\: form\: is\: between\: pK_{a2}\: and\: pK_{a3}\: so\: pI=\dfrac{3.8+8.3}{2}=6.05}\]
c) Write out the name of this peptide using the one and three letter codes.
CIDK, CysIleAspLys
7. An enzyme catalyzed reaction was carried out in a solution buffered with 0.060 M histidine, pH 6.3. As a result of the reaction, the pH fell to 5.7. (use \(\mathrm{pK_{a}}\) values: \(\alpha\)-COOH = 1.82, imidazole side chain = 6.0, and \(\alpha\)-NH2 = 9.17).
a) How much acid (moles/liter) was produced as the result of the reaction?
\[\mathbf{Initial:\: 6.3=6.0+log\dfrac{[His^{0}]}{[His^{+}]}}\]
\[\mathbf{10^{0.3}=\dfrac{[His^{0}]}{[His^{+}]}=2}\]
\[\mathbf{[His^{0}]+[His^{+}]=0.06\:M}\]
\[\mathbf{3[His^{+}]=0.06\: M}\]
\[\mathbf{[His^{+}]=0.02\: M}\]
\[\mathbf{[His^{0}]=0.04\: M}\]
\[\mathbf{Final: \: 5.7=6.0+log\dfrac{[His^{0}]}{[His^{+}]}}\]
\[\mathbf{\dfrac{[His^{0}]}{[His^{+}]}=0.5}\]
\[\mathbf{[His^{0}]+[His^{+}]=0.06\: M}\]
\[\mathbf{1.5[His^{+}]=0.06\: M}\]
\[\mathbf{[His^{+}]=0.04\: M}\]
\[\mathbf{[His^{0}]=0.02\: M}\]
The acid produced is equal to the amount of \(\mathbf{His^{0}}\) that is converted to \(\mathbf{His^{+}}\) this is 0.04 - 0.02 = 0.02 M
b) What would the pH have been at the end of the reaction if it had been carried out in plain water instead of the 0.060 M histidine buffer?
\[\mathbf{0.02\: M\: acid\: (H^{+})\: in\: H_{2}O; \: pH=-log[H^{+}]=-log0.02\: M=1.7}\]
8. Aldolase catalyzes the conversion of fructose-1,6-bisphosphate (F-1,6-BP) to dihydroxyacetone phosphate (DHAP) and glyceraldehyde-3-phosphate (G-3-P). The \(\ \mathrm{\Delta G^{\circ’}}\) for the reaction is +5.7 kcal/mol at \(\mathrm{37^{\circ}C}\).
a) The steady state concentrations given below were measured in red blood cells at \(\mathrm{37^{\circ}C}\). Calculate the \(\mathrm{\Delta G}\) value for aldolase under these conditions.
\[\begin{matrix} \mathrm{[F-1,6-BP]} & = & \mathrm{3.5\times 10^{-5}\: M}\\ \mathrm{[DHAP]} & = & \mathrm{1.4\times 10^{-4}\: M}\\ \mathrm{[G-3-P]} & = & \mathrm{2.1\times 10^{-5}\: M} \end{matrix}\]
\[\mathbf{\Delta G= \Delta G^{\circ’}+RT ln\dfrac{[DHAP][G-3-P]}{[F-1,6-BP]}}\]
\[\mathbf{=5.7+1.98\times 10^{-3}\dot 310 ln\dfrac{(1.4\times 10^{-4})(2.1\times 10^{-5})}{(3.5\times 10^{-5})}=-0.06kcal/mol}\]
b) In which direction is the aldolase reaction proceeding under the steady state conditions given in a)? (Note: Your answer must be consistent with your answer in a)).
Forward at \(\mathbf{37^{\circ}C}\) because \(\mathbf{\Delta G}\) is negative.
c) In which direction does the aldolase reaction proceed under biochemical standard state conditions?
At standard state, \(\mathbf{\Delta G =\Delta G^{\circ’} = +5.7 kcal/mol}\), the reaction proceeds in the reverse direction.
d) During the reaction catalyzed by aldolase, the amino side chain of a lysine residue on the protein reacts with a keto group of F-1,6-BP. The lysine amino group must be unprotonated in order to react. Calculate the fraction of the lysine side chains that you would expect to be unprotonated at pH 7. (The \(\mathrm{pK_{a}}\) of a lysine side chain is 10.5).
\[\begin{matrix} \mathbf{pH=pK_{a}+log\dfrac{[K]}{[KH^{+}]}} & \mathbf{[K]+[KH^{+}]=1}\\ \mathbf{7.0=10.5+log\dfrac{[K]}{[KH^{+}]}}& \mathbf{1.000316[KH^{+}]=1}\\ \mathbf{-3.5=log\dfrac{[K]}{[KH^{+}]}}& \mathbf{therefore,\: [KH^{+}]=1}\\ \mathbf{\dfrac{[K]}{[KH^{+}]}=3.6\times 10^{-4}} & \mathbf{and\: [K]=3.16\times 10^{-4}}\\ \mathbf{[K]=3.16\times 10^{-4}[KH^{+}]}& \mathbf{therefore,\: 3.16\times 10^{-4}\: of\: the\: lysine\: is\: unprotonated} \end{matrix}\]

